Equations of Ellipses in Standard Form: Foci on the $y$-axis

In an earlier lesson, the equation of an ellipse with center at the origin and foci on the $x$-axis was derived, in great detail.

You may want to review this earlier lesson before studying the ‘in-a-nutshell’ derivation here.

Derivation of Ellipse Equation: Center at the Origin, Foci on the $y$-axis

Although it is much shorter, this derivation should look strikingly familiar to the earlier derivation.

Notice also that the variables $\,a\,,$ $\,b\,$ and $\,c\,$ have the same meaning as in the earlier derivation, and the relationship between these three variables is the same.

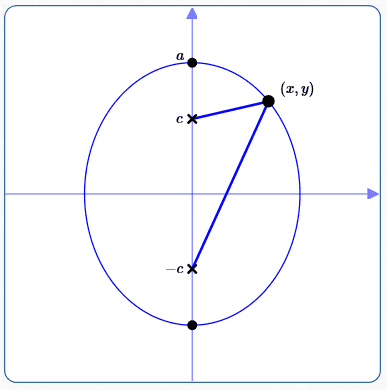
Position the Ellipse

As shown above, position an ellipse with center at the origin and foci (marked with ‘x’) on the $y$-axis.

Notation ($\,c\,$ and $\,a\,$)

Define:

$c = \,$ the distance from the center (the origin) to each focus.

Since $\,c\,$ is a distance, $\,c \gt 0\,.$ The coordinates of the foci are therefore $\,(0,c)\,$ and $\,(0,-c)\,.$
$a = \,$ the distance from the center to each vertex.

Since $\,a\,$ is a distance, $\,a \gt 0\,.$ The coordinates of the vertices are therefore $\,(0,a)\,$ and $\,(0,-a)\,.$

Ellipse Constant

The ellipse constant is the length of the major axis, which is $\,2a\,.$

Use the Definition of Ellipse on a Typical Point

Let $\,(x,y)\,$ be a typical point on the ellipse, so that the sum of its distances to the foci is the ellipse constant ($\,2a\,$). That is,

$$ \begin{align} &\biggl( \text{distance from } (x,y) \text{ to } (0,-c) \biggr)\cr &\quad + \biggl( \text{distance from } (x,y) \text{ to } (0,c) \biggr)\cr &= 2a \end{align} $$

Use the distance formula and make obvious simplications:

$$ \begin{align} &\sqrt{\bigl(x - 0\bigr)^2 + \bigl(y-(-c)\bigr)^2}\cr &\quad + \sqrt{\bigl(x - 0\bigr)^2 + \bigl(y-c\bigr)^2}\cr &= 2a \end{align} $$

$$\begin{align} &\sqrt{x^2 + (y+c)^2}\cr &\quad + \sqrt{x^2 + (y-c)^2}\cr &= 2a \end{align} $$

Isolate, Undo, Repeat

$$ \begin{align} &\sqrt{x^2 + (y+c)^2}\cr &\quad = 2a - \sqrt{x^2 + (y-c)^2} \end{align} $$

$$ \cssId{s28}{\text{(Isolate the first square root)}} $$

$$ \begin{align} &x^2 + (y+c)^2\cr &\quad = 4a^2 - 4a\sqrt{x^2 + (y-c)^2}\cr &\qquad + x^2 + (y-c)^2 \end{align} $$

$$ \cssId{s30}{\text{(Square both sides and simplify)}} $$

$$ \begin{align} &\color{red}{x^2} + \color{red}{y^2} + 2cy + \color{red}{c^2}\cr &\quad = 4a^2 - 4a\sqrt{x^2 + (y-c)^2}\cr &\qquad + \color{red}{x^2} + \color{red}{y^2} - 2cy + \color{red}{c^2} \end{align} $$

$$ \cssId{s32}{\text{(FOIL)}} $$

$$ \begin{align} &2cy\cr &\quad = 4a^2 - 4a\sqrt{x^2 + (y-c)^2}\cr &\qquad - 2cy\cr \end{align} $$

$$ \cssId{s34}{\text{(Addition property of equality)}} $$
$$ \begin{gather} \cssId{s35}{a\sqrt{x^2 + (y-c)^2} = a^2 - cy}\cr \cssId{s36}{\substack{\textstyle\text{(Isolate square root term}\\ \textstyle\text{and divide by $\,4$)}}} \end{gather} $$
$$ \begin{gather} \cssId{s37}{a^2 \bigl( x^2 + (y-c)^2 \bigr) = (a^2 - cy)^2} \cr \cssId{s38}{\text{(Square both sides and simplify)}} \end{gather} $$

$$ \begin{align} &a^2 \bigl( x^2 + y^2 - 2cy + c^2 \bigr)\cr &\quad = a^4 - 2a^2cy + c^2y^2 \end{align} $$

$$ \cssId{s40}{\text{(FOIL)}} $$

$$ \begin{align} &a^2x^2 + a^2y^2 \color{red}{- 2a^2cy} + a^2c^2\cr &\quad = a^4 \color{red}{- 2a^2cy} + c^2y^2 \end{align} $$

$$ \cssId{s42}{\text{(Distributive law)}} $$

$$ \begin{align} &a^2x^2 + a^2y^2 - c^2y^2\cr &\quad = a^4 - a^2c^2 \end{align} $$

$$ \cssId{s44}{\substack{\textstyle\text{(Addition property of equality}\\ \textstyle\text{and re-arrange)}}} $$
$$ \begin{gather} \cssId{s45}{a^2x^2 + (a^2 - c^2)y^2 = a^2(a^2 - c^2)}\cr \cssId{s46}{\text{(Factor)}} \end{gather} $$

Define $\,b\,$; Get Relationship Between $\,a\,,$ $\,b\,$ and $\,c$

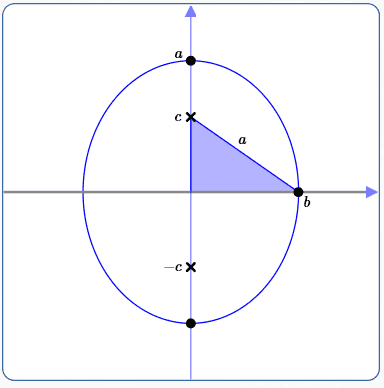
relationship between a, b, and c in ellipse

As before, define $\,b\,$ as the distance from the center to an endpoint of the minor axis. Then, $\,c^2 + b^2 = a^2\,.$ Equivalently, $\,b^2 = a^2 - c^2\,$ and $\,c^2 = a^2 - b^2\,.$

Again, $\,a \gt b\,.$

Rewrite Equation to Eliminate $\,c\,,$ and Simplify

$$ \begin{gather} \cssId{s53}{a^2x^2 + b^2y^2 = a^2b^2}\cr\cr \cssId{s54}{\frac{a^2x^2}{a^2b^2} + \frac{b^2y^2}{a^2b^2} = \frac{a^2b^2}{a^2b^2}}\cr\cr \cssId{s55}{\frac{x^2}{b^2} + \frac{y^2}{a^2} = 1} \end{gather} $$

Summary

The equation of an ellipse with center at the origin and foci along the $y$-axis is

$$ \cssId{s58}{\frac{x^2}{b^2} + \frac{y^2}{a^2} = 1} $$

where:

$a \gt b \gt 0$
The length of the major axis (which lies on the $y$-axis) is $\,2a\,.$
The length of the minor axis (which lies on the $x$-axis) is $\,2b\,.$
The foci are determined by solving the equation $\,c^2 = a^2 - b^2\,$ for $\,c\,.$ The coordinates of the foci are $\,(0,-c)\,$ and $\,(0,c)\,.$
Note: the foci are on the $\color{red}{y}$-axis, and the bigger number ($\,a^2 \gt b^2\,$) is beneath the $\,\color{red}{y}^2\,.$

Alternative Approach for Foci on the $y$-axis: Reflecting or Rotating

Once we have the equation for foci on the $x$-axis $\left(\frac{x^2}{a^2} +\frac{y^2}{b^2} = 1\right)\,,$ there are shorter and easier ways to get the equation for foci on the $y$-axis $\left(\frac{x^2}{b^2} +\frac{y^2}{a^2} = 1\right)\,.$

We didn't really have to go through this derivation again (although it's good practice).

Here are two ways. For ease of reference, let $\,\cal G\,$ denote the graph of $\,\frac{x^2}{a^2} +\frac{y^2}{b^2} = 1\,.$

The two transformations used below are discussed in greater detail in this earlier optional lesson.

(1) Reflect $\,\cal G\,$ About the Line $\,y = x$

Reflection about the line $\,y = x\,$ switches the coordinates of a point: $\,(x,y)\,$ moves to $\,(y,x)\,.$

In an equation, this is accomplished by switching the variables $\,x\,$ and $\,y\,.$

Switching $\,x\,$ and $\,y\,$ turns $\,\frac{x^2}{a^2} +\frac{y^2}{b^2} = 1\,$ into $\,\frac{y^2}{a^2} +\frac{x^2}{b^2} = 1\,.$

Done!

(2) Rotate $\,\cal G\,$ Counterclockwise by $\,90^\circ$

Counterclockwise rotation by $\,90^\circ\,$ moves the point $\,(x,y)\,$ to the new point $\,(-y,x)\,.$

In an equation, this is accomplished by:

Replacing every $\,x\,$ by $\,y$
Replacing every $\,y\,$ by $\,-x$

These replacements turn $\,\frac{x^2}{a^2} +\frac{y^2}{b^2} = 1\,$ into:

$$ \begin{gather} \cssId{s88}{\frac{y^2}{a^2} +\frac{(-x)^2}{b^2} = 1}\cr\cr \cssId{s89}{\frac{y^2}{a^2} + \frac{x^2}{b^2} = 1} \end{gather} $$

Easy!

Note: The exercises in this lesson cover ellipses with centers at the origin and both foci along the $x$-axis and foci along the $y$-axis.