Changing Decimals to Fractions

Consider again the place values in the base ten number system.
If we move from left to right, notice that the place value is successively divided by ten:

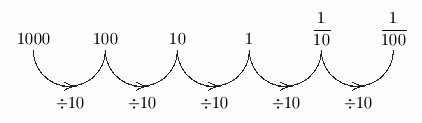
place values to the right of the decimal point

$\frac{1000}{10} = 100\,$; the thousands place is followed by the hundreds place
$\frac{100}{10} = 10\,$; the hundreds place is followed by the tens place
$\frac{10}{10} = 1\,$; followed by the ones place

This pattern continues, after first putting a decimal point to the right of the ones place:

one divided by ten is one-tenth;
the first place to the right of the decimal point is the tenths place;
one-tenth divided by ten is one-hundredth;
the second place to the right of the decimal point is the hundredths place; and so on.

Be certain to notice the difference between hundred and hundredth.
Hundred is to the left of the decimal point, and hundredth is to the right of the decimal point.

The place values are ‘mirrored’ about the ones place, adding ‘th’ to the right of the decimal point:

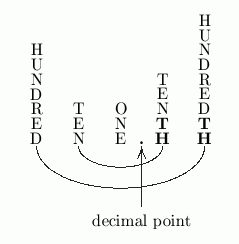
The first place to the right of the decimal point has place value $\displaystyle\,\frac{1}{10^1} = \frac{1}{10}\,$.

The second place to the right of the decimal point has place value $\displaystyle\,\frac{1}{10^2} = \frac{1}{100}\,$.

In general, the $\,n^{\text{th}}\,$ place to the right of the decimal point has place value $\displaystyle\,\frac{1}{10^n}\,$.

A base ten number that uses a decimal point is called a decimal.
Thus, $\,2.5\,$ and $\,0.0003\,$ and $\,3.0\,$ are called decimals, but $\,3\,$ (no decimal point) is not called a decimal.

In particular, notice that the word decimal has to do with the name being used for a number, not the number itself!
The numbers $\,3.0\,$ and $\,3\,$ live at the same place on a number line; they are equal; they are the same number.
However, $\,3.0\,$ is a decimal, whereas $\,3\,$ is not a decimal.

If there are no digits to the left of the decimal point, then it is good practice to put a zero in the ones place.
That is, write $\;0.02\;$ (with zero in the ones place), not $\;.02\;$ (with nothing in the ones place).

To read decimals aloud, start by using the prior rules for reading the part to the left of the decimal point.
Read the decimal point as and.
Only the right-most place value is used for reading the part to the right of the decimal point, as illustrated in the following examples:

read $\,2.03\,$ as two and three hundredths
read $\,23.457\,$ as twenty-three and four hundred fifty-seven thousandths
read $\,0.000042\,$ as forty-two millionths

Notice that the word and should ONLY be used for the decimal point.
Resist the temptation to insert the word and anywhere else!

Reading a decimal like $\,972.28936\,$ following the rules above gets a bit tedious:
nine hundred seventy-two and twenty-eight thousand nine hundred thirty-six hundred-thousandths. (Yuck!)
Thus, it is often read as nine hundred seventy-two point two, eight, nine, three, six.
That is, say point to represent the decimal point, and then just read each digit, separately, that follows the decimal point.

The number $\,0.237\,$ can be viewed as $$ 2\cdot\frac{1}{10} + 3\cdot\frac{1}{100} + 7\cdot\frac{1}{1000} $$ or can alternately be viewed as $$ 237\cdot\frac{1}{1000} = \frac{237}{1000}\;. $$

Recall that in a fraction $\displaystyle\,\frac{N}{D}\,$, the top ($\,N\,$) is called the numerator and the bottom ($\,D\,$) is called the denominator.

For example, in the fraction $\displaystyle\,\frac{23}{100}\,$, the numerator is $\,23\,$ and the denominator is $\,100\,$.

To go from a a decimal to a fraction, you use the right-most place value to determine the correct denominator;
the entire number (without the decimal point) becomes the numerator.
In particular, the number of zeros in the denominator is the same as the number of places to the right of the decimal point.

EXAMPLES:

$0.0013 = \frac{13}{10000}\;$;
four places to the right of the decimal point; four zeros in the denominator

$23.107 = \frac{23107}{1000}\;$;
three places to the right of the decimal point; three zeros in the denominator

$0.72 = \frac{72}{100}\;$;
two places to the right of the decimal point; two zeros in the denominator

If you're rusty on fractions, don't worry—they will be reviewed in future sections, starting here.

Master the ideas from this section
by practicing the exercise at the bottom of this page.

When you're done practicing, move on to:
Multiplying and Dividing Decimals by Powers of Ten

In this web exercise, you will practice renaming decimals as fractions.
Don't simplify any fractions: leave $\,0.4\,$ as $\,\frac{4}{10}\,$, instead of reducing it to $\,\frac{2}{5}\,$.

Use a forward slash ( $\;/\;$ ) to indicate a fraction: for example, $\,0.032\,$ gets renamed as $\,32/1000\,$.

Do NOT insert commas in any numbers: type in $\;32/1000\;$, not $\;32/1,000\;$.

Use the last reported place value for your new name, even if it is zero:
for example, report $\;0.50\;$ as $\;50/100\;$, not $\;5/10\;$.

(an even number, please)