Identifying Place Values

The system that we use to represent numbers is wonderfully efficient and simple. Large numbers can be represented with very few symbols in a neat and organized way.

The method rests on two concepts, base and place value, which are briefly discussed in the next few paragraphs. The concepts are introduced using base three for simplicity. Then, the concepts are extended to our base ten number system.

The concept of base is best represented by grouping. Imagine a factory where objects are being packaged for shipment around the world. Workers are instructed to ‘bundle things up’ every time they get a group of three.

Here are the names for the packaging that they use:

a set of three objects is called a packet
a set of three packets (which is $\,3\cdot 3 = 9\,$ objects) is called a box
a set of three boxes (which is $\,3\cdot 9 = 27\,$ objects) is called a carton

Notice that a packet holds $\,3^1 = 3\,$ objects; a box holds $\,3^2 = 9\,$ objects; and a carton holds $\,3^3 = 27\,$ objects.

Suppose a shipment of $\,46\,$ objects is to go out to Lenox, Massachusetts. How would these $\,46\,$ objects get bundled? First, bundle up one carton, leaving $\,46 - 27 = 19\,$ objects remaining. Then, bundle up two boxes, leaving $\,19 - 2\cdot 9 = 1\,$ object remaining.

Thus, $\,46\,$ items get bundled into one carton, two boxes, no packets, and one object, as shown below:

The workers use a shorthand to keep track of how orders get bundled. The record for this shipment of $\,46\,$ looks like this:

The workers read this aloud as: ‘one, two, zero, one; base three’

Each position (place value) represents a power of $\,3\,$:

the right-most place value is:	$3^0 = 1$	(objects)
one to the left is:	$3^1 = 3$	(packets)
one more to the left is:	$3^2 = 9$	(boxes)
one more to the left is:	$3^3 = 27$	(cartons)

(Here, you're getting a preview of exponent notation, which will be explored in a future section.)

Of course, bigger shipments would require more place values, and more names for packaging types. This is called a base three number system, because things are bundled in groups of three.

The number system that we use is called the base ten number system. It uses identical concepts, except that things are bundled in groups of ten.

Here are the first few place values and their names in our base ten number system:

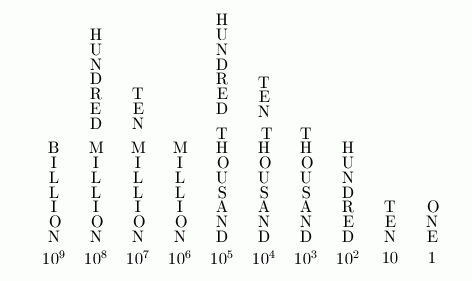
Notice that the right-most place value is $\,1\,,$ and you just keep multiplying by $\,10\,$ as you move to the left.

For example, the base ten number $\,23{,}487\,$ represents:

$ \begin{align} &23{,}487 \\ &\quad = 2\cdot 10^4 + 3\cdot 10^3 + 4\cdot 10^2 + 8\cdot 10^1 + 7\cdot 10^0\cr\cr &\quad = 2\cdot 10{,}000 + 3\cdot 1{,}000 + 4\cdot 100 + 8\cdot 10 + 7\cdot 1 \cr\cr &\quad = 2\,\text{ ten-thousands} + 3\,\text{ thousands} + 4\,\text{ hundreds}\cr &\qquad + 8\,\text{ tens} + 7\,\text{ ones} \end{align} $

Practice

This exercise gives you practice recognizing place values.