Sine and Cosine as Scaling Factors of Hypotenuse

When you work with right triangles, it's convenient to use sine and cosine to ‘scale’ the hypotenuse and give you the lengths of the shorter sides.

This is the simple thought process:

Want the side adjacent to a known angle $\,\theta\,$? Scale the hypotenuse by $\,\cos\theta\,,$ giving $\,h\cos\theta\,.$
Want the side opposite a known angle $\,\theta\,$? Scale the hypotenuse by $\,\sin\theta\,,$ giving $\,h\sin\theta\,.$

The sketches below illustrate the idea.

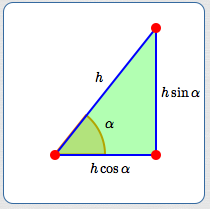
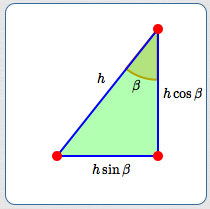
scale the hypotenuse using cosine to get a side adjacent to an angle; scale by sine to get side opposite

Getting Scaling Factors from the Right Triangle Definitions of Sine and Cosine

These scaling factors are an immediate consequence of the right triangle definitions of sine and cosine:

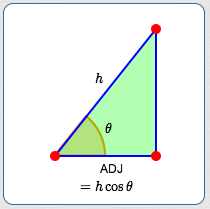
Want the side adjacent to $\,\theta\,$? Scale the hypotenuse by $\,\cos\theta\,$:

$$ \begin{gather} \cssId{s11}{\cos\theta = \frac{\text{ADJ}}{h}}\cr\cr \cssId{s12}{\text{ADJ} = h\cos\theta} \end{gather} $$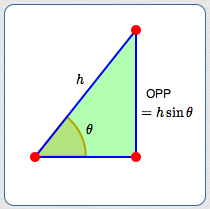

Want the side opposite $\,\theta\,$? Scale the hypotenuse by $\,\sin\theta\,$:

$$ \begin{gather} \cssId{s15}{\sin\theta = \frac{\text{OPP}}{h}}\cr\cr \cssId{s16}{\text{OPP} = h\sin\theta} \end{gather} $$

Given a right triangle with known hypotenuse and one known acute angle, you should immediately be able to write down exact lengths for the remaining two sides.

You shouldn't have to pass through the extra step of thinking:

$$ \begin{gather} \cssId{s19}{\text{sine} = \frac{\text{OPP}}{\text{HYP}}}\cr\cr \cssId{s20}{\text{or}}\cr\cr \cssId{s21}{\text{cosine} = \frac{\text{ADJ}}{\text{HYP}}} \end{gather} $$

Getting Scaling Factors from the Unit Circle Definitions of Sine and Cosine

The scaling factors are also an immediate consequence of the unit circle definitions of sine and cosine. To get the desired right triangle with hypotenuse $\,h\,$ and acute angle $\,\theta\,,$ start with a similar right triangle inside the unit circle. Then, scale it to the correct size, as follows:

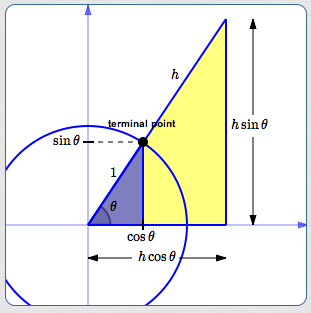
getting scaling factors from the unit circle viewpoint

Lay off the acute angle $\,\theta\,$ in the unit circle. The hypotenuse of the blue triangle has length $\,1\,.$

By definition:

The $x$-value of the terminal point is $\,\cos\theta$
The $y$-value of the terminal point is $\,\sin\theta$

Consequently, in the blue triangle:

The side adjacent to $\,\theta\,$ has length $\,\cos\theta$
The side opposite from $\,\theta\,$ has length $\,\sin\theta$

Scale the blue triangle by a factor of $\,h\,,$ giving the yellow triangle. That is, all three sides of the blue triangle get multiplied by $\,h\,.$

Consequently, in the yellow triangle:

The hypotenuse has length $\,h\,$
The side adjacent to $\,\theta\,$ has length $\,h\cos\theta\,$ (so the hypotenuse has been scaled by $\,\cos\theta\,$)
The side opposite from $\,\theta\,$ has length $\,h\sin\theta\,$ (so the hypotenuse has been scaled by $\,\sin\theta\,$)

Summary

Suppose you're given a right triangle with known hypotenuse $\,h\,$ and one known acute angle $\,\theta\,.$

The remaining two sides are shorter than the hypotenuse. How much shorter?

Well, $\,0 \lt \cos\theta \lt 1\,.$ The side adjacent to $\,\theta\,$ has length $\,h\cos\theta\,.$ So, $\,\cos\theta\,$ gives the appropriate ‘shrinking factor’ for the adjacent side!

Also, $\,0 \lt \sin\theta \lt 1\,.$ The side opposite from $\,\theta\,$ has length $\,h\sin\theta\,.$ So, $\,\sin\theta\,$ gives the appropriate ‘shrinking factor’ for the opposite side!