Reflecting Property of a Hyperbola (Part 2)

(This page is Part 2. Click here for Part 1.)

Set-Up/Notation for Understanding the Reflecting Property of a Hyperbola

The reflecting property of a hyperbola will be proved for a hyperbola in standard form, with foci on the $x$-axis.

As derived in Equations of Hyperbolas in Standard Form, such a hyperbola has:

Equation of the form $\,\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1\,$ (where $\,a\,$ and $\,b\,$ are positive constants)
The foci are $\,(c,0)\,$ and $\,(-c,0)\,,$ where $\,c\,$ is the positive number satisfying $\,c^2 = a^2 + b^2$

Refer to the sketch below for additional set-up:

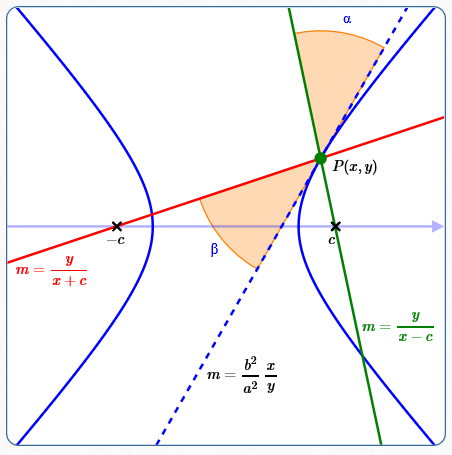
additional notation for derivation of a hyperbola in standard form

Let $\,P(x,y)\,$ be a typical point on the (right branch of) the hyperbola.

The ‘outside light directed towards one focus’ is shown as the green line. The slope of the green line, from the focus $\,(c,0)\,$ to $\,P(x,y)\,,$ is:

$$ \begin{align} &\text{slope of green line}\cr\cr &\quad = \frac{y_2-y_1}{x_2-x_1}\cr\cr &\quad = \frac{y-0}{x-c}\cr\cr &\quad = \frac{y}{x-c} \end{align} $$

The red line connects the other focus, $\,(-c,0)\,,$ to $\,P(x,y)\,.$ The slope of the red line is:

$$ \begin{align} &\text{slope of red line}\cr\cr &\quad = \frac{y_2-y_1}{x_2-x_1}\cr\cr &\quad = \frac{y-0}{x-(-c)}\cr\cr &\quad = \frac{y}{x+c} \end{align} $$

The tangent line to the hyperbola at $\,P(x,y)\,$ is shown dashed. Borrowing a result from Calculus, the slope of this tangent line is $\,\frac{b^2}{a^2}\,\frac{x}{y}\,.$ For those of you who know Calculus, the details are given here. For others—preview the incredible power of Calculus!

Use implicit differentiation on $\,\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1\,$:

$$ \cssId{s19}{\frac{2x}{a^2} - \frac{2y}{b^2}\frac{dy}{dx} = 0} $$

Solve for $\frac{dy}{dx}\,$ (the slope):

$$\cssId{s21}{\frac{dy}{dx}} \cssId{s22}{= \frac{-2x}{a^2}\cdot\frac{b^2}{-2y}} \cssId{s23}{= \frac{b^2}{a^2}\frac{x}{y}}$$

What Needs To Be Shown

The outside light ‘hits’ the tangent line (dashed) at $\,P(x,y)\,$ and is reflected. By the physics Law of Reflection:

The red line is the path of reflected light
if and only if
$\alpha = \beta$

In other words, both of the following are true:

If reflected light follows the red line (and thus passes through the other focus), then angle $\,\alpha\,$ equals angle $\,\beta\,.$
If $\,\alpha = \beta\,,$ then reflected light follows the red line (and thus passes through the other focus).

Therefore:

To prove the reflecting property of the hyperbola, we will show that $\,\alpha = \beta\,.$

Both $\,\alpha\,$ and $\,\beta\,$ are positive angles, not exceeding $\,90^\circ\,.$ The tangent function is one-to-one between $\,0^\circ\,$ and $\,90^\circ\,,$ so if $\,\tan\alpha = \tan\beta\,,$ it follows that $\,\alpha = \beta\,.$ Consequently:

To prove the reflecting property of the hyperbola, we will show that $\,\tan\alpha = \tan\beta\,.$

Summarizing results for convenience:

[Hyperbola]

The hyperbola under investigation has equation $\,\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1\,.$ The positive number $\,c\,$ satisfies $\,c^2 = a^2 + b^2\,.$

[Green Line]

The green line is outside light directed towards the focus $\,(c,0)\,.$ This green line has slope $\,\frac{y}{x-c}\,,$ where $\,(x,y)\,$ are the coordinates of the point $\,P\,$ where the green line intersects the hyperbola.

[Red Line]

The red line is between point $\,P(x,y)\,$ and the second focus, $\,(-c,0)\,.$ This red line has slope $\,\frac{y}{x+c}\,.$

[Tangent/Dashed Line]

The dashed line is the tangent to the hyperbola at $\,P(x,y)\,.$ It has slope $\,\frac{b^2}{a^2}\frac{x}{y}\,.$

Using the formula for the tangent of the angle between two intersecting lines of known slope:

Angle $\,\alpha$

The angle $\,\alpha\,$ is formed by the intersecting green and tangent lines. The green line has the greater angle of inclination. Thus:

$$ \cssId{s56}{\tan\alpha = \frac{\frac{y}{x-c} - \frac{b^2}{a^2}\frac{x}{y}}{1 + \frac{y}{x-c}\cdot\frac{b^2}{a^2}\cdot\frac{x}{y}}} $$

Angle $\,\beta$

The angle $\,\beta\,$ is formed by the intersecting red and tangent lines. The tangent line has the greater angle of inclination. Thus:

$$ \cssId{s60}{\tan\beta = \frac{\frac{b^2}{a^2}\frac{x}{y} - \frac{y}{x+c}}{1 + \frac{b^2}{a^2}\cdot\frac{x}{y}\cdot\frac{y}{x+c}}} $$

Now—breathe deeply—and verify that the following equations are equivalent. The final equation is true, since $\,(x,y)\,$ lies on the hyperbola $\,\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1\,.$ Therefore, the first equation is also true, completing the proof!

$$ \tan\alpha = \tan\beta $$

We're trying to show this is true

$$ \frac{\frac{y}{x-c} - \frac{b^2}{a^2}\frac{x}{y}}{1 + \frac{\color{red}{y}}{x-c}\cdot\frac{b^2}{a^2}\cdot\frac{x}{\color{red}{y}}} = \frac{\frac{b^2}{a^2}\frac{x}{y} - \frac{y}{x+c}}{1 + \frac{b^2}{a^2}\cdot\frac{x}{\color{red}{y}}\cdot\frac{\color{red}{y}}{x+c}} $$

Substitute formulas from above

$$ \frac{\frac{y}{x-c} - \frac{b^2}{a^2}\frac{x}{y}}{1 + \frac{x}{x-c}\cdot\frac{b^2}{a^2}} = \frac{\frac{b^2}{a^2}\frac{x}{y} - \frac{y}{x+c}}{1 + \frac{b^2}{a^2}\cdot\frac{x}{x+c}} $$

Cancel

$$ \begin{align} &\frac{a^2y(x-c)}{a^2y(x-c)}\left(\frac{\frac{y}{x-c} - \frac{b^2}{a^2}\frac{x}{y}}{1 + \frac{x}{x-c}\cdot\frac{b^2}{a^2}}\right)\cr\cr &\quad = \left(\frac{\frac{b^2}{a^2}\frac{x}{y} - \frac{y}{x+c}}{1 + \frac{b^2}{a^2}\cdot\frac{x}{x+c}}\right)\frac{a^2y(x+c)}{a^2y(x+c)} \end{align} $$

Clear complex fractions

$$ \frac{a^2y^2 - b^2x(x-c)}{a^2(x-c)y + b^2xy} = \frac{b^2x(x+c) - a^2y^2}{a^2(x+c)y + b^2xy} $$

Multiply out, re-arrange factors

$$ \begin{align} &\bigl(a^2y^2 - b^2x(x-c)\bigr) \bigl(a^2(x+c)y + b^2xy\bigr)\cr\cr &\quad = \bigl(a^2(x-c)y + b^2xy\bigr) \bigl(b^2x(x+c) - a^2y^2\bigr) \end{align} $$

Cross-multiply

$$ \begin{align} &\bigl(a^2y^2 - b^2x^2 + b^2xc\bigr) \bigl(a^2xy + a^2cy + b^2xy\bigr)\cr\cr &\quad = \bigl(a^2xy - a^2cy + b^2xy\bigr) \bigl(b^2x^2 + b^2xc - a^2y^2\bigr) \end{align} $$

Distributive law

$$ \begin{align} &a^4xy^3 \color{purple}{+ a^4cy^3} + a^2b^2xy^3\cr &\qquad - a^2b^2x^3y \color{red}{- a^2b^2cx^2y} - b^4x^3y\cr &\qquad \color{red}{\,+\, a^2b^2cx^2y} + a^2b^2c^2xy \color{grey}{+ b^4cx^2y}\cr\cr &\quad = a^2b^2x^3y \color{orange}{+ a^2b^2cx^2y} - a^4xy^3\cr &\qquad \color{orange}{- a^2b^2cx^2y} - a^2b^2c^2xy \color{purple}{+ a^4cy^3}\cr &\qquad + b^4x^3y \color{grey}{+ b^4cx^2y} - a^2b^2xy^3 \end{align} $$

Distributive law

$$ \begin{align} &\color{blue}{a^4xy^3} + \color{blue}{a^2b^2xy^3}\cr &\qquad \color{green}{- a^2b^2x^3y - b^4x^3y}\cr &\qquad + a^2b^2c^2xy\cr\cr &\quad = \color{green}{a^2b^2x^3y} \color{blue}{- a^4xy^3}\cr &\qquad - a^2b^2c^2xy\cr &\qquad \color{green}{+ b^4x^3y} \color{blue}{- a^2b^2xy^3} \end{align} $$

Delete red/orange/purple/grey terms

$$ \begin{align} &\color{blue}{xy^3(2a^4 + 2a^2b^2)}\cr &\qquad + \color{green}{x^3y(-2a^2b^2 - 2b^4)}\cr &\qquad + xy(2a^2b^2c^2)\cr &\quad = 0 \end{align} $$

Gather like terms on left side

$$ \begin{align} &y^2(a^4 + a^2b^2)\cr &\qquad + x^2(-a^2b^2 - b^4)\cr &\qquad + a^2b^2c^2\cr &\quad = 0 \end{align} $$

Divide by $\,2xy$

$$ \begin{align} &y^2a^2(a^2 + b^2)\cr &\qquad - x^2b^2(a^2 + b^2)\cr &\qquad + a^2b^2c^2\cr &\quad = 0 \end{align} $$

Factor

$$ y^2a^2c^2 - x^2b^2c^2 + a^2b^2c^2 = 0 $$

Since $\,a^2 + b^2 = c^2$

$$ - y^2a^2 + x^2b^2 - a^2b^2 = 0 $$

Multiply by $\,-1\,,$ divide by $\,c^2$

$$ x^2b^2 - y^2a^2 = a^2b^2 $$

Re-arrange

$$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$

Divide by $\,a^2b^2$

Hooray! Isn't it wonderful when simplicity emerges from seeming chaos?