Polar Coordinates (Part 2)

(This page is Part 2. Click here for Part 1.  Click here for Part 3.)

Simple Curves in Polar Coordinates

Different coordinate systems make different curves extremely easy to plot:

Rectangular Coordinate System:

• Vertical lines:  $\,x = \text{some #}$
• Horizontal lines:  $\,y = \text{some #}$

Polar Coordinate System:

• Circles centered at the pole:  $\,r = \text{some #}$
• Lines through the pole:  $\,\theta = \text{some #}$

Example

Graph:

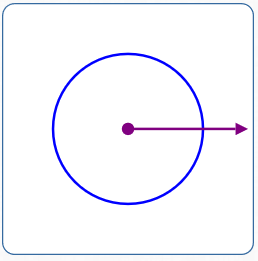
Equation/Description:  $\cssId{s11}{r = 3}\,,$ circle with radius $\,3\,,$ centered at the pole.

Comments:  This is an equation in two variables: $$\cssId{s15}{r \color{red}{+ 0\cdot\theta} = 3}\,$$

The graph is (using set-builder notation): $$\cssId{s17}{\{\,(3,\theta) \ \ |\ \ \theta\in\Bbb R\,\}}$$

Example

Graph:

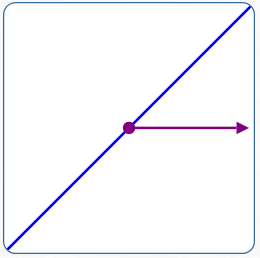
Equation/Description: $\,\theta = \frac{\pi}4\,$ (or $\,\theta = 45^\circ\,$), line through the pole.

Comments:  This is an equation in two variables:

The graph is:

Converting from Polar Coordinates to Rectangular Coordinates

Given a point with polar coordinates $\,(r,\theta)\,,$ we want formulas for the rectangular coordinates $\,(x,y)\,.$ That is, we want:

• a formula for $\,x\,$ that depends on $\,r\,$ and $\,\theta\,$
• a formula for $\,y\,$ that depends on $\,r\,$ and $\,\theta\,$

Here's the punchline:  For all real numbers $\,r\,$ and $\,\theta\,,$

The details follow.

To convert from polar to rectangular coordinates, first introduce a rectangular coordinate system:

• $x$-axis: the line through the polar axis; positive direction is the direction of the polar axis
• $y$-axis: the line through the pole, perpendicular to the $x$-axis; positive direction corresponds to a $\,90^\circ\,$ counterclockwise rotation of the polar axis
• Note that the origin of the rectangular coordinate system is the pole.

For convenience, the conventional orientations are shown below. Note:  You could position the rectangular coordinate system relative to the polar axis in many different ways. For different placements, however, the resulting formulas might be very complicated!

Use the polar axis to introduce a rectangular coordinate system

Plot a Point in Polar Coordinates ($\,r \ge 0\,$) and Find its Rectangular Coordinates

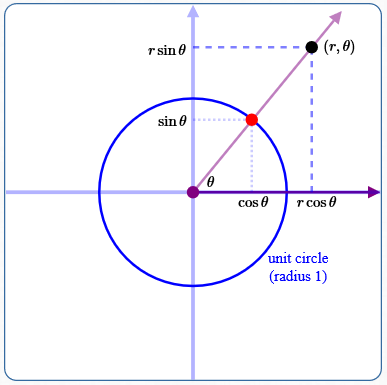
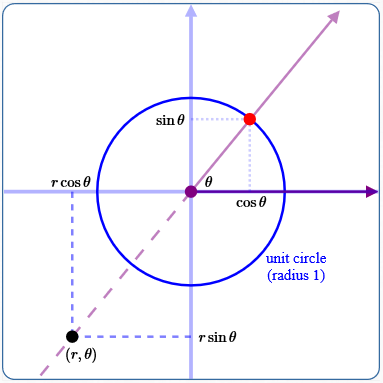
Let $\,r\,$ and $\,\theta\,$ be real numbers, with $\,r\ge 0\,.$ (The case $\,r \lt 0\,$ is given below.)

The blue circle shown above is the unit circle (radius $\,1\,$).

Consider the point with polar coordinates $\,(r,\theta)\,,$ shown above in black.

The rotated ray is shown above in light purple. It does not matter how $\,\theta\,$ is ‘swept out’ to get this rotated ray! All that matters for this discussion is the intersection of the rotated ray and the unit circle (shown in red) .

Since $\,r\ge 0\,$ (by assumption), the black point $\,(r,\theta)\,$ actually lies on the rotated ray.

Note:

• If $\,r \gt 1\,,$ then $\,(r,\theta)\,$ lies outside the unit circle (as shown below).
• If $\,r = 1\,,$ then $\,(r,\theta)\,$ lies on the unit circle.
• If $\,r \lt 1\,,$ then $\,(r,\theta)\,$ lies inside the unit circle.

By the definition of sine and cosine, the red point has rectangular coordinates $\,(\cos\theta\,,\,\sin\theta)\,.$

Scale the coordinates of the red point by the nonnegative number $\,r\,$ to get the coordinates of the black point: $\,(r\cos\theta\,,\,r\sin\theta)\,.$

Getting rectangular coordinates for a point with polar coordinates $\,(r,\theta)\,$:
$\,r\ge 0\,$

Plot a Point in Polar Coordinates ($\,r \lt 0\,$) and Find its Rectangular Coordinates

Let $\,r\,$ and $\,\theta\,$ be real numbers, with $\,r \lt 0\,.$ Everything is the same as the case above, with the minor modifications given next.

Since $\,r\lt 0\,$ (by assumption), the black point $\,(r,\theta)\,$ lies a distance $\,|r|\,$ from the pole on the opposite side of the rotated ray.

Note:

• If $\,|r| \gt 1\,,$ then $\,(r,\theta)\,$ lies outside the unit circle (as shown above).
• If $\,|r| = 1\,,$ then $\,(r,\theta)\,$ lies on the unit circle.
• If $\,|r| \lt 1\,,$ then $\,(r,\theta)\,$ lies inside the unit circle.

By the definition of sine and cosine, the red point has rectangular coordinates $\,(\cos\theta\,,\,\sin\theta)\,.$

Scale the coordinates of the red point by the negative number $\,r\,$ to get the coordinates of the black point: $\,(r\cos\theta\,,\,r\sin\theta)\,.$

Since the scaling number is negative, the coordinates change sign. If an unscaled coordinate is positive, the scaled coordinate is negative. If an unscaled coordinate is negative, the scaled coordinate is positive.

Thus, a point in Quadrant I moves to a point in Quadrant III. A point in Quadrant II moves to a point in Quadrant IV... and so on!

Getting rectangular coordinates for a point with polar coordinates $\,(r,\theta)\,$:
$\,r\lt 0\,$

Summarizing both cases, we have: