 Polar Coordinates (Part 3)
Polar Coordinates (Part 3)
(This page is Part 3. Click here for Part 1. Click here for Part 2.)
Converting from Rectangular Coordinates to Polar Coordinates
Given a point with rectangular coordinates $\,(x,y)\,,$ we want formulas for polar coordinates $\,(r,\theta)\,.$ That is, we want:
- a formula for $\,r\,$ that depends on $\,x\,$ and $\,y$
- a formula for $\,\theta\,$ that depends on $\,x\,$ and $\,y$
Here's part of the punchline: For all real numbers $\,x\,$ and $\,y\,$:
$$\cssId{s7}{r = \sqrt{x^2 + y^2}}$$Unfortunately, $\,\theta\,$ is considerably more complicated! The details follow.
To convert from rectangular to polar coordinates, first introduce a polar axis. The formulas are simplest by placing the pole at the origin, with the ray pointing in the direction of the positive $x$-axis.
Since every point has infinitely many names in polar coordinates, decisions need to be made about which names to return!
Formula for $\,r$
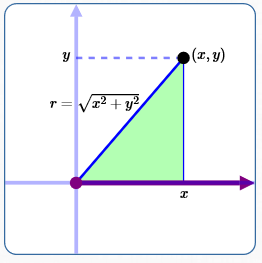
As the sketch above suggests, there's an easy formula to get a point's distance from the origin:
$$\cssId{s16}{r = \sqrt{x^2 + y^2}}$$The table below verifies that the expression $\,\sqrt{x^2 + y^2}\,$ returns the correct distance from the origin for every point in the plane.
Recall that for all real numbers $\,t\,$:
- $|t|\,$ gives the distance from $\,t\,$ to zero
- $\sqrt{t^2} = |t|$
- $|t|^2 = t^2\,$
| Point(s) $\,(x,y)\,$: | the origin: $\,(0,0)\,$ |
| Distance from $\,(x,y)\,$ to origin: | $\color{red}{0}$ |
| The expression $\,\sqrt{x^2 + y^2}\,$ gives: | $\begin{align}&\sqrt{x^2 +y^2}\cr &\quad = \sqrt{0^2 + 0^2} = \color{red}{0}\end{align}$ |
| Point(s) $\,(x,y)\,$: | $x$-axis: $\,(x,0)\,$ |
| Distance from $\,(x,y)\,$ to origin: | $\color{red}{|x|}$ |
| The expression $\,\sqrt{x^2 + y^2}\,$ gives: | $\begin{align}&\sqrt{x^2 +y^2}\cr &\quad = \sqrt{x^2 + 0^2}\cr &\quad = \sqrt{x^2} = \color{red}{|x|}\end{align}$ |
| Point(s) $\,(x,y)\,$: | $y$-axis: $\,(0,y)\,$ |
| Distance from $\,(x,y)\,$ to origin: | $\color{red}{|y|}$ |
| The expression $\,\sqrt{x^2 + y^2}\,$ gives: | $\begin{align}&\sqrt{x^2 +y^2}\cr &\quad = \sqrt{0^2 + y^2}\cr &\quad = \sqrt{y^2} = \color{red}{|y|}\end{align}$ |
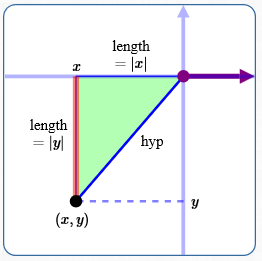
| Point(s) $\,(x,y)\,$: | Four quadrants: $\,(x,y)\,$ for $\,x\ne 0\,$ and $\,y\ne 0$ |
| Distance from $\,(x,y)\,$ to origin: |
See sketch above:
Drop a perpendicular from the point to the $x$-axis. The right triangle thus formed has side lengths $\,|x|\,$ and $\,|y|\,.$ Using the Pythagorean theorem:
$$\begin{align}(\text{hyp})^2
&= |x|^2 + |y|^2\cr &= x^2 + y^2
\end{align}$$
$$\cssId{s41}{\text{hyp} = \color{red}{\sqrt{x^2 + y^2}}}$$
|
| The expression $\,\sqrt{x^2 + y^2}\,$ gives: | $\color{red}{\sqrt{x^2 + y^2}}$ |
Formulas for $\,\theta$
Using the formula $\,r = \sqrt{x^2 + y^2}\,$ guarantees that $\,r\,$ is nonnegative.
With nonnegative $\,r\,,$ there are two conventional choices for $\,\theta\,$ to get unique names for all points in the plane:
- $0 \le \theta \lt 2\pi$
- $-\pi \lt \theta \le \pi$
Formula for $\,\theta\,$ in Quadrant I
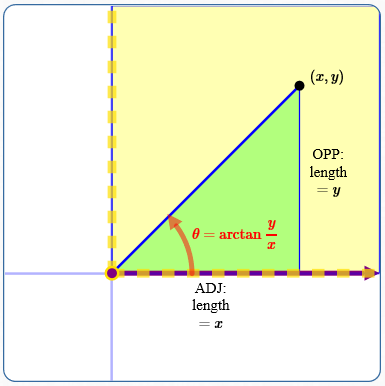
Quadrant I (where $\,x \gt 0\,$ and $\,y \gt 0\,$) is no problem!
Given a point $\,(x,y)\,$ in Quadrant I, the right triangle shown above always has these properties:
- For polar coordinates, we need $\,\color{red}{\theta}\,.$
- The side OPPosite $\,\color{red}{\theta}\,$ has length $\,y\,.$
- The side ADJacent to $\,\color{red}{\theta}\,$ has length $\,x\,.$
- Thus, $\,\color{red}{\tan \theta = \frac{\text{OPP}}{\text{ADJ}} = \frac yx}\,.$
In Quadrant I, $\,\color{red}{\theta}\,$ is always (strictly) between $\,0\,$ and $\,\frac\pi 2\,.$ So, we want the angle between $\,0\,$ and $\,\frac\pi 2\,$ whose tangent is $\,\frac yx\,.$ In this case, the arctangent gives us precisely the angle we want!
Formulas for $\,\theta\,$ in Other Quadrants
Since (by definition) the arctangent function always returns angles in the interval $\,(-\frac{\pi}2\,,\,\frac{\pi}2)\,,$ once we leave Quadrant I, the formulas for $\,\theta\,$ may require some ‘tweaking’.
As you'll see next, the formula for $\,\theta\,$ is a piecewise-defined function—with quite a few pieces!

Quadrant I: $\,x \gt 0\,$ and $\,y \gt 0\,$
In this quadrant: $\displaystyle\theta = \arctan \frac yx$
Piecewise-Defined Function that Returns $\,\theta\in [0,2\pi)\,$ for Points $\,(x,y)$
These sketches are used to get the different ‘pieces’ for the piecewise-defined function. In all sketches, the black point has rectangular coordinates $\,(x,y)\,.$
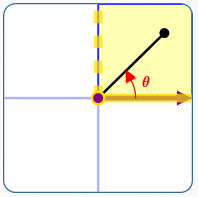
$\,x \gt 0\,$ and $\,y\ge 0$
Here: $\displaystyle\,\frac yx \ge 0$
$\displaystyle\,\color{red}{\theta = \arctan{\frac yx}}$
Note: $\displaystyle\,\theta\in [0,\frac\pi 2)$
Note: when $\,y = 0\,,$
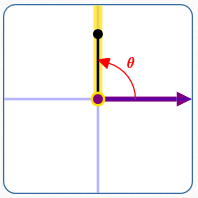
$\,x = 0\,$ and $\,y\gt 0$
Here: $\displaystyle\,\frac yx\,$ is not defined
$\displaystyle\,\color{red}{\theta = \frac\pi 2}\,$
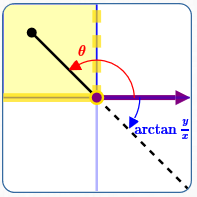
$x \lt 0\,$ and $\,y\ge 0$
Here: $\displaystyle\,\frac yx \le 0$
$\displaystyle\,\color{red}{\theta = (\arctan{\frac yx}) + \pi}\,$
Note: $\displaystyle\,\theta\in (\frac\pi 2,\pi]$
Note: when $\,y = 0\,,$
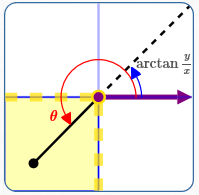
$x \lt 0\,$ and $\,y\lt 0$
Here: $\displaystyle\,\frac yx \gt 0$
$\displaystyle\,\color{red}{\theta = (\arctan{\frac yx}) + \pi}$
Note: $\displaystyle\,\theta\in (\pi,\frac{3\pi}2)$
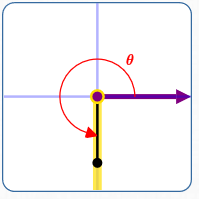
$x = 0\,$ and $\,y\lt 0$
Here: $\displaystyle\,\frac yx\,$ is not defined
$\displaystyle\color{red}{\theta = \frac{3\pi}{2}}$
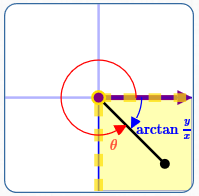
$x \gt 0\,$ and $\,y\lt 0$
Here: $\displaystyle\,\frac yx \lt 0$
$\displaystyle\color{red}{\theta = (\arctan{\frac yx}) + 2\pi}\,$
Note: $\displaystyle\,\theta\in (\frac{3\pi}2,2\pi)$
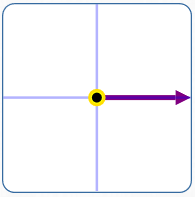
$x = 0\,$ and $\,y = 0$
Here: $\displaystyle\,\frac yx\,$ is not defined
$\displaystyle\color{red}{\theta = 0}$
Note: For uniqueness, we can agree that the point with rectangular coordinates $\,(0,0)\,$ gets represented only by $\,r = 0\,$ and $\,\theta = 0\,.$
The piecewise-defined description of $\,\theta\,$ is given below.
Similarly, you can find formulas for $\,\theta\,$ when the desired angles to be returned are in the interval $\,(-\pi,\pi]\,.$
This formula for $\,\theta\,,$ together with $\,r = \sqrt{x^2 + y^2}\,,$ gives a unique representation $\,(r,\theta)\,$ for each point with rectangular coordinates $\,(x,y)\,.$
The angles $\,\theta\,$ are in the interval $\,[0,2\pi)\,.$
$$ \cssId{s111}{\theta = \cases{ 0 &if $\,x = 0\,$ and $\,y = 0\,$\cr\cr \arctan\frac yx &if $\,x \gt 0\,$ and $\,y \ge 0\,$\cr\cr \frac\pi 2 &if $\,x = 0\,$ and $\,y \gt 0\,$\cr\cr \pi +\arctan\frac yx &if $\,x \lt 0\,$\cr\cr \frac{3\pi} 2 &if $\,x = 0\,$ and $\,y \lt 0\,$\cr\cr 2\pi +\arctan\frac yx &if $\,x \gt 0\,$ and $\,y \lt 0\,$ }} $$Flowers, Spirals, and More
There are many fun/
Spirals (and more)
Below, $\,r\,$ is a simple linear function of $\,\theta\,$:
$$\cssId{s117}{r = m\theta + b\,, \ \ \text{ for } \theta\in [\theta_{\text{start}},\theta_{\text{end}}]}$$Type in Desired Values for the Curve $\,r = m\theta + b$
| $m\,$: | $b\,$: |
| $\theta_{\text{start}}\,$ (radians): | $\theta_{\text{end}}\,$ (radians): |
$r = m\theta + b$, for $\, \theta\in [\theta_{\text{start}},\theta_{\text{end}}]$
Change parameters by setting values and clicking the ‘Plot the curve!’ button.
Three points are given:
- The blue point is the start point: $\,r_\text{start} := m\theta_{\text{start}} + b$
- The green point is the end point: $\,r_\text{end} := m\theta_{\text{end}} + b$
-
The red point is a glider on the curve.
Drag it around!
Rectangular coordinates are ‘attached to’ the point. Corresponding polar coordinates are displayed at the top right of the graph (with $\,\theta\,$ between $\,-180^\circ\,$ and $\,180^\circ\,$).
Note that:
- $m\,$ controls how fast $\,r\,$ changes: When $\,\theta\,$ changes by an amount $\,\Delta\theta\,,$ then $\,r\,$ changes by $\,m\Delta\theta\,.$ That is, $\,r\,$ changes $\,m\,$ times faster than $\,\theta\,.$
- $b\,$ gives an ‘offset’: When $\,\theta = 0\,,$ then $\,r = m(0) + b = b\,.$
- The viewing screen changes as needed, so that you can see the entire curve. If you change a value and it looks like the graph hasn't changed—check the scales on the $x$ and $y$ axes!
Here are some for you to try:
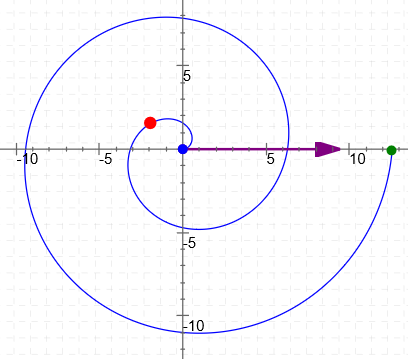
$r = \theta\,,$ for $\,\theta\in [0,4\pi]$
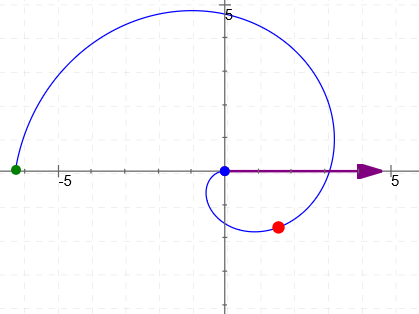
$r = -\theta\,,$ for $\,\theta\in [0,2\pi]$
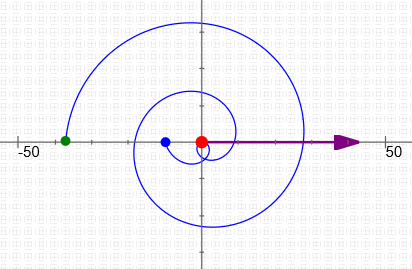
$r = 3\theta - 10\,,$ for $\,\theta\in [0,5\pi]$
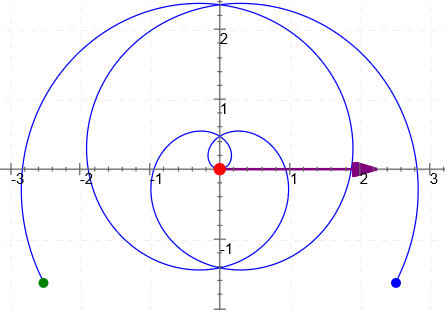
$r = 0.3\,\theta\,,$ for $\,\theta\in [-10,10]$
Flowers (and more)
Of course, WolframAlpha can plot polar curves! Here are some for you to try—you can cut-and-paste the text below each image (if desired).
Polar Rose: $\,r = a\cos(k\theta)$
($\,a\,$ gives the length of the petals)
Gives a rose with $\,k\,$ petals when $\,k\,$ is an odd integer (for $\,\theta\in [0,\pi]\,$)
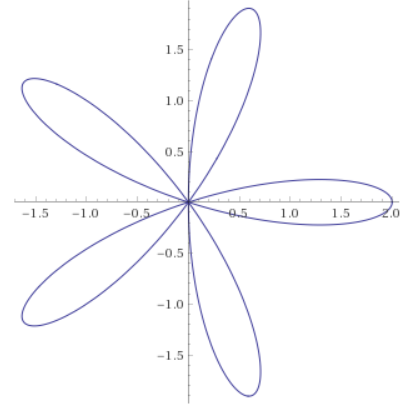
r = 2cos(5theta), with theta from 0 to pi
Gives a rose with $\,2k\,$ petals when $\,k\,$ is an even integer (for $\,\theta\in [0,2\pi]\,$)
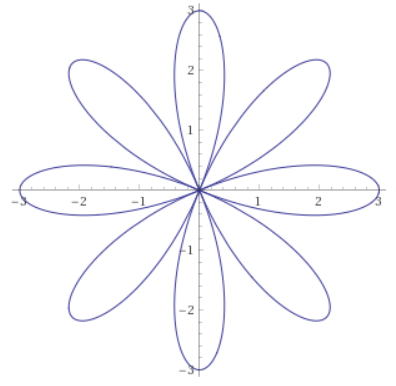
r = 3cos(4theta), with theta from 0 to 2pi
Just Have Fun!
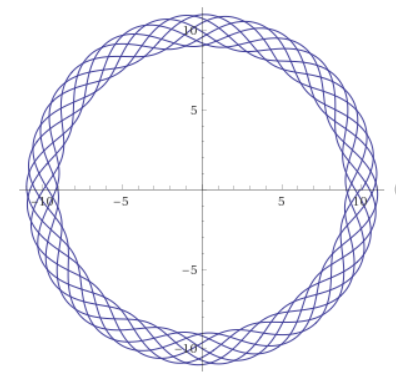
r = 10 + sin(2*pi*theta), for theta from 0 to 14pi
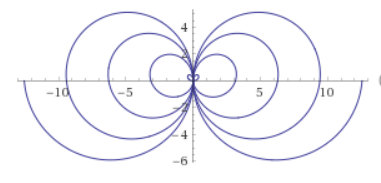
r = theta * cos(theta), for theta from -4pi to 4pi
You can cut-and-paste the text above into WolframAlpha, and then play around!