audio read-through Parabolas: Definition, Reflectors/Collectors, Derivation of Equations

Parabolas were introduced in the Algebra II curriculum. Links to these earlier lessons are given below, together with concepts that you must know from each section.

Be sure to check your understanding by doing some of each problem type in these earlier exercises. These concepts are then further explored in this current lesson.

Parabolas

You must know the:

Equations of Simple Parabolas

Play With Parabolas

You can play with parabolas below:

Move the focus:

Move the directrix:

Below is some information that wasn't covered in the Algebra II curriculum. The exercises on this page address only this new information. However, it is assumed that you've mastered the exercises from the two earlier parabola lessons (Parabolas and Equations of Simple Parabolas).

Axis of Symmetry for a Parabola

Recall that a parabola is determined by two pieces of information:

The axis of symmetry for a parabola is the line through the focus that is perpendicular to the directrix. If the parabola is ‘folded’ along this line, then ‘half’ the parabola perfectly coincides with the other half.

All conic sections have (at least one) axis of symmetry. For the standard forms of conics, the axes of symmetry are always the $x$-axis and/or the $y$-axis.

For the standard form $\,x^2 = 4py\,$ of a parabola, the axis of symmetry is the $y$-axis.

For the standard form $\,y^2 = 4px\,$ of a parabola (derived next), the axis of symmetry is the $x$-axis.

Deriving the Standard Form $\,y^2 = 4px\,$ For a Parabola

Place a parabola with its vertex at the origin, as shown below.

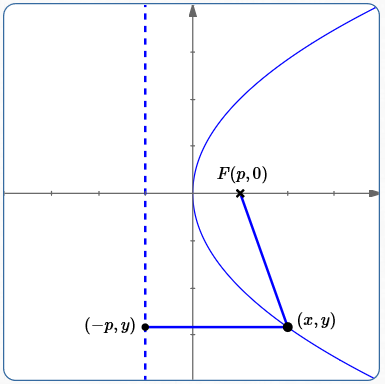
a parabola

If we put the focus on the $x$-axis, then the directrix will be parallel to the $y$-axis. Why? The axis of symmetry passes through the vertex (the origin) and the focus, hence is the $x$-axis. The directrix is perpendicular to the axis of symmetry.

Or, if we put the directrix parallel to the $y$-axis, then the focus will be on the $x$-axis. Why? The axis of symmetry is perpendicular to the directrix and contains the vertex (the origin), hence is the $x$-axis. The focus always lies on the axis of symmetry.

In either case, let $\,p \ne 0\,$ denote the $x$-value of the focus. Thus, the focus has coordinates $\,(p,0)\,.$

Although the sketch below shows the situation where $\,p\gt 0\,,$ the following derivation also holds for $\,p \lt 0\,.$

a parabola

Since the vertex is a point on the parabola, the definition of parabola dictates that it must be the same distance from the focus and the directrix.

Thus, the directrix must cross the $x$-axis at $\,-p\,$; indeed, every $x$-value on the directrix equals $\,-p\,.$

Let $\,(x,y)\,$ denote a typical point on the parabola.

The distance from $\,(x,y)\,$ to the focus $\,(p,0)\,$ is found using the distance formula:

$$ \begin{align} &\sqrt{(x-p)^2 + (y-0)^2 }\cr &\qquad = \sqrt{(x-p)^2 + y^2} \tag{1} \end{align} $$
a parabola

To find the distance from $\,(x,y)\,$ to the directrix, first drop a perpendicular from $\,(x,y)\,$ to the directrix. This perpendicular intersects the directrix at $\,(-p,y)\,.$ The distance from $\,(x,y)\,$ to the directrix is therefore the distance from $\,(x,y)\,$ to $\,(-p,y)\,$:

$$ \begin{align} &\sqrt{(x-(-p))^2 + (y-y)^2}\cr &\qquad = \sqrt{(x+p)^2} \tag{2} \end{align} $$

From the definition of parabola, distances $\,(1)\,$ and $\,(2)\,$ must be equal:

$$ \cssId{s77}{\sqrt{(x-p)^2 + y^2} = \sqrt{(x+p)^2}} $$

This equation simplifies considerably, as follows:

Squaring both sides:

$$\cssId{s80}{(x-p)^2 + y^2 = (x+p)^2}$$

Multiplying out:

$$\cssId{s82}{x^2 - 2px + p^2 + y^2 = x^2 + 2px + p^2}$$

Subtracting $\,x^2 + p^2\,$ from both sides:

$$\cssId{s84}{y^2 - 2px = 2px}$$

Adding $\,2px\,$ to both sides:

$$ \cssId{s86}{y^2 = 4px} $$

This is the second standard form for a parabola, where the axis of symmetry is the $x$-axis. The most critical thing to notice is the coefficient of $\,x\,,$ since it holds the key to locating the focus of the parabola .

As an example, consider the equation $\,y^2 = 10x\,.$ Comparing with $\,y^2 = 4px\,,$ we see that $\,10 = 4p\,,$ or $\,p = \frac{10}4 = \frac 52\,.$ Thus, $\,y^2 = 10x\,$ graphs as a parabola with vertex at the origin and focus $\,(\frac 52,0)\,.$

Standard Forms for Parabolas

In summary, we have:

Standard Form of Parabola $x^2 = 4py$
Axis of Symmetry $y$-axis
Vertex $(0,0)$
Focus $(0,p)$
Directrix $y = -p$
Standard Form of Parabola $y^2 = 4px$
Axis of Symmetry $x$-axis
Vertex $(0,0)$
Focus $(p,0)$
Directrix $x = -p$

Sketching Parabolas

You do not need to memorize lots of things to sketch parabolas in standard form! The key thing to memorize is that the important coefficient is $\,4p\,,$ where the size (absolute value) of $\,p\,$ gives the distance from the focus to the origin.

You'll be letting the equation tell you the proper shape, as indicated next:

Recognize Form

Recognize that you have an equation of the form $\,x^2 = 4py\,$ or $\,y^2 = 4px\,.$ If needed, find the discriminant to jog your memory: $\,B^2 - 4AC = 0\,$ indicates a parabola.

There's only one interesting coefficient in these equations ($\,4p\,$), so it is referred to as ‘the coefficient’ below.

Isolate Squared Term

Isolate the squared term. That is, get the squared term (with a coefficient of $\,1\,$) all by itself on one side of the equation.

Determine Shape (Opening Up/Down/Left/Right)

Since a perfect square is always nonnegative, the other side of the equation must also be nonnegative. Depending on the equation, this will force one of the following four situations:

The examples below illustrate how this works.

Use this information to (lightly) sketch the proper shape. Remember that the vertex is the origin.

Plot the Focus

The focus is always inside the parabola. To find its distance from the origin, throw away any minus signs (as needed) on the coefficient and divide by $\,4\,.$ Why? The coefficient is $\,4p\,,$ and $\,|p|\,$ gives the distance from the focus to the origin.

Or, you can set the coefficient to $\,4p\,$ and solve for $\,p\,$ (which will include the correct sign).

Draw in the Directrix

Sketch the directrix. It is the same distance from the origin as the focus, on the opposite side.

Plot Easy Points to Get the Proper ‘Width’

There are always three easy points to get on a parabola, once you know the focus and the directrix. Refer to the sketch below.

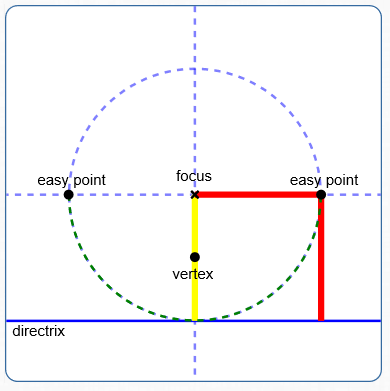
three easy points on a parabola three easy points on a parabola

Three easy points on a parabola: the vertex; two points to give a sense of the ‘width’

Example 1

Graph: $\,y^2 = 3x$

Solution

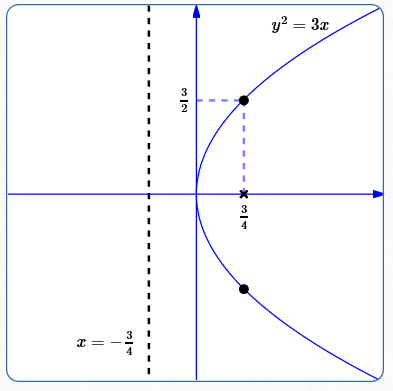
a parabola example

The equation $\,y^2 = 3x\,$ is in the form $\,y^2 = 4px\,.$

The $\,y^2\,$ term is already isolated, with a coefficient of $\,1\,.$

$$ \begin{align} &y^2\ge 0\cr &\quad \implies 3x\ge 0\cr &\quad \implies x\ge 0 \end{align} $$

Thus, the $x$-value of every point on the parabola is nonnegative; the parabola opens to the right.

$$ \begin{align} &4p = 3\cr &\quad \implies p = \frac 34\cr &\quad \implies \text{focus } = (\frac 34,0) \end{align} $$

Equation of directrix: $\,x = -\frac 34\,$

Two Easy Points

Distance from focus to directrix:  $\,2(\frac 34) = \frac 32\,$

Coordinates of easy points:  $\,(\frac 34,\frac 32)\,$ and $\,(\frac 34,-\frac 32)$

It's confidence-boosting to check that these points satisfy the equation $\,y^2 = 3x\,$:

$$\begin{gather} \cssId{s175}{\bigl(\pm \frac 32\bigr)^2\ \ \overset{?}{=}\ \ 3\bigl(\frac 34\bigr)}\cr\cr \cssId{s176}{\frac 94 = \frac 94}\quad \cssId{s177}{\text{Yep!}} \end{gather} $$

Example 2

Graph: $\,2x^2 + 5y = 0$

Solution

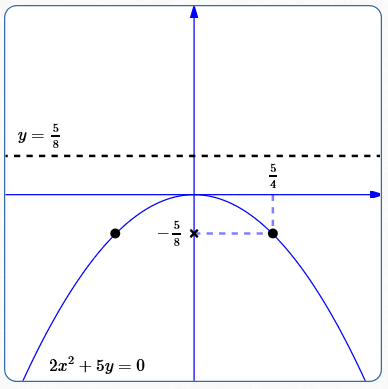
a parabola example

The equation $\,2x^2 + 5y = 0\,$ has only $\,x^2\,$ and $\,y\,$ terms. It can be put in the form $\,x^2 = 4py\,.$

Isolate the square term, and get a coefficient of $\,1\,$:

$$ \begin{gather} \cssId{s184}{2x^2 + 5y = 0}\cr\cr \cssId{s185}{2x^2 = -5y}\cr\cr \cssId{s186}{x^2 = -\frac 52y} \end{gather} $$
$$ \begin{align} &x^2\ge 0\cr &\quad \implies -\frac 52y\ge 0\cr &\quad \implies y\le 0 \end{align} $$

Thus, the $y$-value of every point on the parabola is negative (or zero); the parabola opens down.

$$ \begin{align} &4p = -\frac 52\cr &\quad \implies p = -\frac 58\cr &\quad \implies \text{focus } = (0,-\frac 58) \end{align} $$

Equation of directrix:  $\,y = \frac 58$

Two Easy Points

Distance from focus to directrix:  $\,2(\frac 58) = \frac 54$

Coordinates of easy points:  $\,(\frac 54,-\frac 58)\,$ and $\,(-\frac 54,-\frac 58)$

It's confidence-boosting to check that these points satisfy the equation $\,2x^2 + 5y = 0\,$:

$$ \begin{gather} \cssId{s199}{2\bigl(\pm \frac 54\bigr)^2 + 5(-\frac 58)\ \ \overset{?}{=}\ \ 0}\cr\cr \cssId{s200}{2\bigl(\frac {25}{16}\bigr) - \frac{25}{8}\ \ \ \overset{?}{=}\ \ 0}\cr\cr \cssId{s201}{0 = 0}\quad \cssId{s202}{\text{Yep!}} \end{gather} $$

Concept Practice