Law of Cosines (Part 2)

(This page is Part 2. Click here for Part 1.)

Proof of the Law of Cosines

The proof of the Law of Cosines is a smidgeon harder than the proof of the Law of Sines, but it's not too bad for such a powerful result.

Here's a re-naming of rectangular coordinates that is needed in the proof:

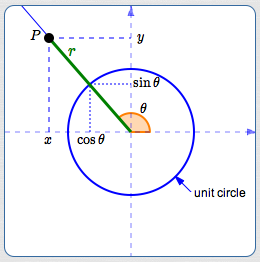
Take any point $\,P(x,y)\,$ in the plane. Recall that $\,P(x,y)\,$ is a convenient notation for a point $\,P\,$ with coordinates $\,(x,y)\,.$
Let $\,r\,$ denote the distance from the origin to $\,P\,.$
Let $\,\theta\,$ be any angle (measured from the positive $x$-axis) with terminal side passing through $\,P\,.$
By similar triangles (see the sketch above):
$$ \begin{gather} \cssId{s8}{x = r\cos\theta}\cr \cssId{s9}{y = r\sin\theta} \end{gather} $$
So, $\,P(x,y) = P(r\cos\theta,r\sin\theta)\,.$ (This is a useful re-naming in many mathematical situations!)

Now, here's the derivation of the Law of Cosines:

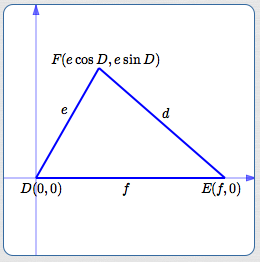
Position Triangle; Name Vertices

Position the triangle in a coordinate plane with one vertex at the origin and one side on the $x$-axis.

Figure out the coordinates of the other two (non-origin) vertices. (Use the result above to find the coordinates for $\,F\,.$ )

Find Distance Between the Two Non-Origin Vertices

Use the distance formula to find the distance between the two (non-origin) vertices.

So that we don't have to deal with square roots, square both sides of the distance formula

$$ \begin{gather} \text{distance between $(x_1,y_1)$ and $(x_2,y_2)$}\cr = \sqrt{(x_2-x_1)^2 + (y_2-y_1)^2} \end{gather} $$

to get:

$$ \cssId{s20}{ {(\text{distance})}^2 = (x_2-x_1)^2 + (y_2-y_1)^2} $$

Note that the distance from $\,E(f,0)\,$ to $\,F(e\cos D,e\sin D)\,$ is $\,d\,.$

Also recall the Pythagorean Identity, which states that $\,\cos^2 \theta + \sin^2\theta = 1\,$ for all angles $\,\theta\,.$

Thus:

$$ \begin{align} \cssId{s24}{d^2}\ &\cssId{s25}{= (\color{blue}{e\cos D} - \color{red}{f})^2 + (\color{blue}{e\sin D} - \color{red}{0})^2}\cr &\quad\cssId{s26}{\text{(distance formula)}}\cr\cr &\cssId{s27}{= e^2\cos^2 D - 2ef\cos D + f^2 + e^2\sin^2 D}\cr &\quad\cssId{s28}{\text{(FOIL)}}\cr\cr &\cssId{s29}{= e^2(\cos^2 D + \sin^2 D) + f^2 - 2ef\cos D}\cr &\quad\cssId{s30}{\text{(factor, re-arrange terms)}}\cr\cr &\cssId{s31}{= e^2(1) + f^2 - 2ef\cos D}\cr &\quad\cssId{s32}{\text{(Pythagorean Identity)}}\cr\cr &\cssId{s33}{= e^2 + f^2 - 2ef\cos D}\cr &\quad\cssId{s34}{\text{Voila!!}} \end{align} $$

QED

Example: Using the Law of Cosines in a SAS Configuration

Consider a triangle with side lengths $\,3\,$ and $\,5\,,$ and an included $\,57^\circ\,$ angle. Prove that this information uniquely defines a triangle, and then solve the triangle.

If using a calculator, store the full accuracy of computed sides/angles. Then, use these (most accurate) stored values in intermediate calculations.

Summarize the values of sides and angles in a table. In the table, round values to one decimal place.

In the solution below, the default accuracy provided by WolframAlpha is reported and used for intermediate calculations.

Solution

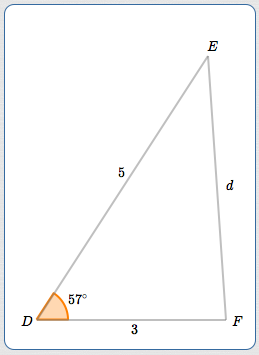
Example: Using the Law of Cosines in a SAS triangle

By SAS, the triangle is unique. The notation above is used in the solution.

Use Law of Cosines

By the Law of Cosines:

$$ \begin{gather} \cssId{s48}{d^2 = 3^2 + 5^2 - 2\cdot 3\cdot 5\cdot\cos 57^\circ}\cr\cr \cssId{s49}{d^2 = 34 - 30\cos 57^\circ}\cr\cr \cssId{s50}{d \approx 4.202} \end{gather} $$

Note: Computation of $\,d\,$ was done by typing in

sqrt(34 - 30cos(57 deg))

at WolframAlpha.

Use Law of Sines (Carefully!)

Now that we have an angle and its opposite side, we can use the Law of Sines. But we have to be careful!

If you're not careful, then you can proceed merrily along, seemingly doing everything right, and end up with a ‘triangle’ that doesn't actually exist.

For example, you might notice that the longest side isn't opposite the biggest angle. Or—if you take the time to check the three Law of Sines ratios—they won't all be the same. A math emergency!

It can be really hard to locate what has gone wrong in the universe.

The well-hidden problem that can occur has to do with the arcsine. When you have a statement like ‘$\,\sin E = 0.5988\,$’ and use the arcsine to find $\,E\,$ (look below—there's a star next to it), this step is fraught with peril!

There are two angles between $\,0^\circ\,$ and $\,180^\circ\,$ (both of which could potentially be angles in a triangle) for which $\,\sin E = 0.5988\,.$ The arcsine only gives you one of them—the acute one. Fine and dandy, if that's the one you want. If you're unlucky, you're on your way to a math emergency.

I'll illustrate such a conundrum in a future section. But, the problem can be avoided, and you need to start developing good habits now.

In any triangle, when comparing angle/opposite side pairs, the shorter side will be opposite the smaller angle.
Given any two angles in any triangle, one of them must be acute. (Why? Otherwise, the angle sum would be greater than $\,180^\circ\,.$ )
When you use the Law of Sines in a situation where you want an acute angle, it will give you the one you want.
When you have a choice, always use the Law of Sines with the shortest side possible.

Okay, now we can get back to work!

$$ \begin{gather} \cssId{s81}{\frac{\sin 57^\circ}{4.202} = \frac{\sin E}{3}}\cr \cssId{s82}{(\text{Use the shorter side!})}\cr\cr \cssId{s83}{\sin E = \frac{3\sin 57^\circ}{4.202} \approx 0.5988}\cr\cr \cssId{s84}{E = \arcsin(0.5988) \approx 36.78^\circ} \quad \cssId{s85}{\bigstar} \end{gather} $$

Find the Remaining Angle

$\,F = 180^\circ - 57^\circ - 36.78^\circ = 86.22^\circ$

Summarize Triangle Information in a Table

Summarize values (with requested rounding) in a table:

Angles	Sides
$D = 57^\circ$	$d = 4.2$
$E = 36.8^\circ$	$e = 3$
$F = 86.2^\circ$	$f = 5$

Use both a rough sketch and the Law of Sines to do a ‘sanity check’. According to the sketch, the values are reasonable. Are the following ratios all approximately the same?

$$ \begin{gather} \cssId{s99}{\frac{\sin 57^\circ}{4.2} \approx 0.1997} \cr\cr \cssId{s100}{\frac{\sin 36.8^\circ}{3} \approx 0.1997} \cr\cr \cssId{s101}{\frac{\sin 86.2^\circ}{5} \approx 0.1996} \cr\cr \end{gather} $$

Okay! (Slight differences may occur due to approximations.)

If you (like me) want everything to be ‘just perfect’ in your mathematical world, then you may have been bothered by the usage of ‘$\,=\,$’ and ‘$\,\approx\,$’ in the previous example. If so, click here!