Triangle Congruence

Due to math content, this page has special requirements (including JavaScript) for full functionality.
With your current viewing scenario, it is not appearing and behaving as it is supposed to!
Please visit Dr. Carol J.V. Fisher's Homepage to learn what this site has to offer.
Watch the "Welcome" video to get started—hope to see you back here soon!

Dr. Carol J.V. Fisher's Homepage

For this exercise, you need ♥ INTERNET EXPLORER 6.0 and above, with MathPlayer installed.♥

TRIANGLE CONGRUENCE

Jump right to the exercises!

Two geometric figures are congruent when they have exactly the same size and shape.
Two geometric figures that are congruent can be superimposed, one on the other, so that they coincide exactly.

The symbol used for congruence is " ≅ ".
For example, the sentence ΔABC≅ ΔDEF is read as "triangle ABC is congruent to triangle DEF ".

When reporting congruences, you must do so in a way that "matches up" corresponding parts.

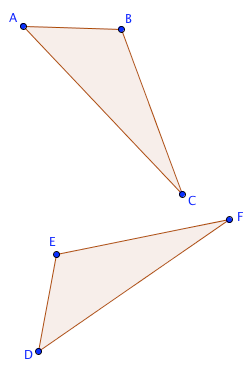
For example, when you report that ΔABC≅ ΔDEF , then all of the following are true:

m∠A=m∠D
m∠B=m∠E
m∠C=m∠F
AB=DE
AC=DF
BC=EF

This property will be referred to as "CPCTC": Corresponding Parts of Congruent Triangles are Congruent.

In this congruence, vertex A corresponds to vertex D .
Vertex B corresponds to vertex E .
Vertex C corresponds to vertex F .

The congruence can be reported in any way that preserves this correspondence between the vertices.
For example, here are two other correct ways that the congruence could be reported:
ΔBAC≅ ΔEDF or ΔCBA≅ ΔFED .

However, ΔBAC≅ ΔDEF is not a correct way to report the congruence indicated above.

When two triangles are congruent, then there is a correspondence such that all three angles have equal measures, and all three sides have equal lengths.
Thus, when two triangles are congruent, there are six "natural" pieces of equal information.
However, to determine that two triangles are congruent, you certainly don't have to specify all six pieces of information!
So—how many, and what types, of information need to be specified to determine that two triangles are congruent?

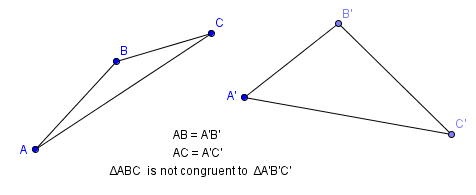
Is it enough to say that two sides are the same?
Clearly not, as the sketch below shows:
no SS congruence

Is it enough to say that two angles are the same?
Well, two angles the same requires all three angles to be the same; is this enough to guarantee congruence?
Clearly not, as the sketch below shows:
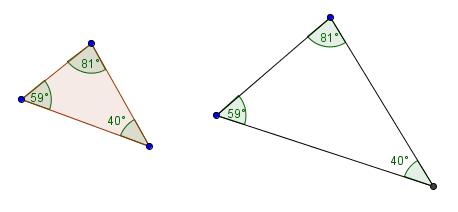
no AA congruence

Triangles with the same angles are said to be similar triangles; one of the triangles is just a "scaled version" of the other.
However, similar triangles do not need to be congruent, because they can be different sizes.
If we additionally specify, however, that one (corresponding) side must be the same,
then this determines the size of the triangle, and forces them to be congruent.

You can specify the side between the two angles, which is called the included side.
This is called ASA (angle-side-angle) congruence.
Notice that the "S" is in the middle, indicating that the side is between the two angles.

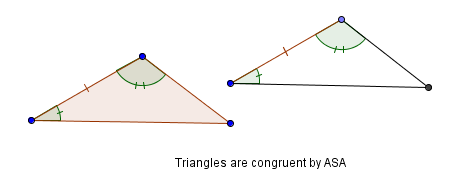
ASA congruence

Or, you can specify one of the two non-included sides.
This is known as AAS (angle-angle-side) congruence.
Notice that the "S" is not between the two "A"s, indicating that the side is not between the two angles.

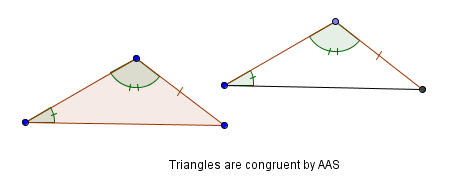
AAS congruence

The precise statements are given below:

THEOREM: ASA CONGRUENCE
A unique triangle is formed by two angles and the included side.
Therefore, if two angles and the included side of one triangle
are congruent to two angles and the included side of another triangle,
then the triangles are congruent.

THEOREM: AAS CONGRUENCE
A unique triangle is formed by two angles and a non-included side.
Therefore, if two angles and the side opposite one of them in a triangle
are congruent to the corresponding parts in another triangle,
then the triangles are congruent.

Next, imagine taking two boards, which can be of different lengths, and attaching them with a hinge at one end.
The hinge can be used to open and close the two boards.
Notice the unique triangle that is formed in this way!
That is, two sides and an included angle uniquely determine a triangle, leading to the "SAS" congruence theorem:

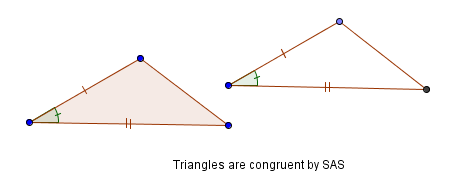
SAS congruence

THEOREM: SAS CONGRUENCE
A unique triangle is formed by two sides and an included angle.
Therefore, if two sides and the included angle of one triangle
are congruent to two sides and the included angle of another triangle,
then the triangles are congruent.

Finally, imagine taking the same two boards you had before, with the hinge between them.
This time, however, you have a third board, which you want to attach to the un-hinged ends.
If the third board isn't too long or too short, then you'll be able to open the hinge just the right amount to attach the third board and form a unique triangle!
This motivation leads to the "SSS" congruence theorem:

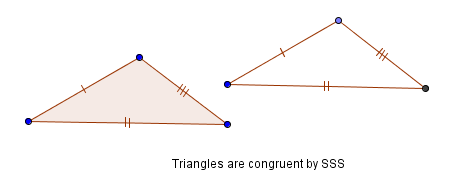
SSS congruence

THEOREM: SSS CONGRUENCE
A unique triangle is formed by specifying three sides of a triangle,
where the longest side (if there is one) is less than the sum of the two shorter sides.
Therefore, if three sides of a triangle are congruent to three sides of another triangle,
then the triangles are congruent.

One final comment. Imagine a triangle with vertices A, B, and C.
(Draw a picture and use it as you read through this discussion.)
Imagine that you are at A, want to travel to C, and can only travel along the sides of the triangle.
There are two routes you can take:
You can go directly from A to C.
Or, you can go from A to B, and then from B to C.
Clearly, the first path must be shorter, since the shortest distance between two points is a straight line!
This discussion leads to an important property of triangles:

THEOREM: THE TRIANGLE INEQUALITY THEOREM
The sum of the lengths of any two sides of a triangle must be greater than the length of the remaining side.
Conversely, if three numbers satisfy the property that the sum of any two of them exceeds the third,
then there exists a triangle with these lengths for its sides.

So, does there exist a triangle with sides of lengths 2, 3, and 6?
No, since 2 + 3 is not greater than 6 .

Does there exist a triangle with sides of lengths 2, 3, and 4?
Yes, since 2 + 3 > 4 , 3 + 4 > 2 , and 4 + 2 > 3 .

On this exercise, you will not key in your answer.
However, you can check to see if your answer is correct.