 Given Two Sides and a Non-Included Angle, How Many Triangles? (Part 2)
Given Two Sides and a Non-Included Angle, How Many Triangles? (Part 2)
(This page is Part 2. Click here for Part 1.)
Introduction to the Arcsine Function and Examples
You might be lamenting:
‘How am I going to remember all these different situations?’
Here's the good news:
The mathematics will tell you which situation you're in (zero, one, or two triangles), providing you do the mathematics correctly!
Let's illustrate with three similar examples. In each, you're given an angle and its opposite side, plus a second side. The key is this—recognize that it is an SSA situation, and be careful!
In all these examples, $\,\beta\,$ denotes the (initially unknown) angle across from the second side.
Example 1: How Many Triangles have a $\,50^\circ\,$ Angle with Opposite Side $\,4\,,$ and Another Side of Length $\,7\,$?
Use the Law of Sines:
$$ \begin{gather} \cssId{s11}{\frac{\sin 50^\circ}{4} = \frac{\sin\beta}{7}}\cr\cr \cssId{s12}{4\sin\beta = 7\sin 50^\circ}\cr\cr \cssId{s13}{\sin\beta = \frac 74\sin 50^\circ \approx 1.34} \end{gather} $$The sine function only takes on values in $\,[-1,1]\,.$ Therefore, there is no angle $\,\beta\,$ with $\,\sin\beta = 1.34\,.$
No triangle exists that meets this SSA situation.
Using the notation of this section, we have $\,a = 4\,,$ $\,\theta = 50^\circ\,,$ and $\,b = 7\,.$
We could have found
$$\,\cssId{s19}{b\sin\theta = 7\sin 50^\circ \approx 5.362}\,$$and noted that $\,a \lt b\sin\theta\,,$ putting us in the ‘no triangle’ category. We didn't need to do this—the mathematics told us!
Example 2: How Many Triangles have a $\,50^\circ\,$ Angle with Opposite Side $\,6\,,$ and Another Side of Length $\,7\,$?
Use the Law of Sines:
$$ \begin{gather} \cssId{s24}{\frac{\sin 50^\circ}{6} = \frac{\sin\beta}{7}}\cr\cr \cssId{s25}{\sin\beta = \frac 76\sin 50^\circ \approx 0.89} \end{gather} $$There are two angles between $\,0^\circ\,$ and $\,180^\circ\,$ with sine equal to $\,0.89\,,$ as shown:
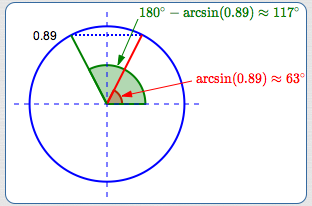
We need to know:
‘What angle(s) have sine equal to $\,0.89\,$?’
The arcsine function (abbreviated as ‘$\,\arcsin\,$’ but still pronounced ‘arc-sign’) helps us to ‘undo’ the sine function! It is discussed in detail in a future section—just briefly introduced here.
By definition:
$$ \begin{align} &\cssId{s33}{\arcsin(x)}\cr &\quad\cssId{s34}{= \text{the angle between $\,-90^\circ\,$ and $\,90^\circ\,$}}\cr &\qquad \cssId{s35}{\text{whose sine is $\,x\,$}} \end{align} $$Therefore, $\,\arcsin(0.89)\,$ is the angle in the first quadrant whose sine value is $\,0.89\,,$ as shown. To find the green angle with sine $\,0.89\,,$ subtract the degree measure of $\,\arcsin(0.89)\,$ from $\,180^\circ\,.$
The possible triangle angle configurations are:
| Given Angle | Angle from Law of Sines | Remaining Angle |
| $50^\circ$ | $\beta = 63^\circ$ | $180^\circ-50^\circ-63^\circ = 67^\circ$ |
| $50^\circ$ | $\beta = 117^\circ$ | $180^\circ-50^\circ-117^\circ = 13^\circ$ |
Using the notation of this section, we have $\,a = 6\,,$ $\,\theta = 50^\circ\,,$ and $\,b = 7\,.$
We could have noted that:
$$ \cssId{s48}{\overbrace{\strut b\sin\theta}^{5.362} } \cssId{s49}{\lt \overbrace{\strut a}^{6} } \cssId{s50}{\lt \overbrace{\strut b}^{7}} $$This puts us in the ‘two triangle’ category. We didn't need to do this—the mathematics told us!
Example 3: How Many Triangles have a $\,50^\circ\,$ Angle with Opposite Side $\,8\,,$ and Another Side of Length $\,7\,$?
Use the Law of Sines:
$$ \begin{gather} \cssId{s55}{\frac{\sin 50^\circ}{8} = \frac{\sin\beta}{7}}\cr\cr \cssId{s56}{\sin\beta = \frac 78\sin 50^\circ \approx 0.67} \end{gather} $$There are two angles between $\,0^\circ\,$ and $\,180^\circ\,$ with sine equal to $\,0.67\,,$ as shown:
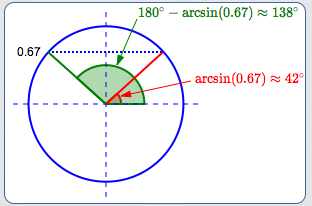
The angle $\,\arcsin(0.67)\approx 42^\circ\,$ is the angle in the first quadrant whose sine value is $\,0.67\,,$ as shown.
The other angle between $\,0^\circ\,$ and $\,180^\circ\,$ with sine equal to $\,0.67\,$ is $\,180^\circ - 42^\circ = 138^\circ\,.$
The potential triangle angle configurations are:
| Given Angle | Angle from Law of Sines | Remaining Angle |
| $50^\circ$ | $\beta = 42^\circ$ | $180^\circ-50^\circ-42^\circ = 88^\circ$ |
| $50^\circ$ | $\beta = 138^\circ$ | $180^\circ-50^\circ-138^\circ = -8^\circ$ |
The second configuration clearly doesn't work! There is only one triangle that satisfies this SSA information.
Using the notation of this section, we have $\,a = 8\,,$ $\,\theta = 50^\circ\,,$ and $\,b = 7\,.$
We could have noted that $\,a \gt b\,,$ putting us in the ‘one triangle’ category. We didn't need to do this—the mathematics told us!
Comments About Notation When Solving Triangles
When naming triangles, it is common to use:
- a capital letter (like $\,D\,$) to denote a vertex
- a lowercase letter (like $\,d\,$) to denote the length of the opposite side
The vertex uniquely identifies the angle at that vertex, and we use this fact to simplify notation. When we write things like ‘$\,\sin D\,$’ or ‘$\,180^\circ - D\,$’, then $\,D\,$ refers to the measure of the angle at vertex $\,D\,.$
Precalculus triangle notation is simpler than Geometry triangle notation. Due to the nature of the work in Geometry, careful distinctions need to be made between points, angles, and numbers:
- A vertex is a point. A vertex is denoted by a capital letter, like $\,P\,.$
- An angle is a geometric object—the union of two rays with a common endpoint. If there's only one angle at a vertex $\,P\,,$ then the angle can be denoted using the symbol $\,\angle P\,.$
- The measure of an angle is a real number. The measure of $\,\angle P\,$ can be denoted by $\,m\angle P\,.$
In Precalculus these distinctions are usually not necessary. It is a nuisance to have to write things like ‘$\,\sin(m\angle P)\,$’. Cumbersome notation (without a need for such) can make simple things look hard.
So—in Precalculus—when there is no possible confusion, we use simple notation and let context determine the correct interpretation.
Here are some Precalculus examples:
- In the expression ‘$\cos D\,$’, $\,D\,$ refers to the measure of an angle.
- In the expression ‘$\,D = 180^\circ - E - F\,$’, $\,D\,$ (and $\,E\,$ and $\,F\,$) refer to measures of angles.
- In the expression ‘$\,\triangle DEF\,$’, $\,D\,$ (and $\,E\,$ and $\,F\,$) refer to points (vertices).
A Complete Example: Using the Law of Sines to Investigate an ‘SSA’ Configuration
Suppose a triangle has a $\,27^\circ\,$ angle with opposite side of length $\,23\,.$ Another side has length $\,30\,.$ If possible, solve the triangle.
Round angles to one decimal place and sides to two decimal places. Any value used inside an arcsine should be rounded to at least four decimal places.
Solution
It's useful to make a sketch to define notation. (Try to do it approximately to scale, but certainly don't measure anything!)
Note that this is an ‘SSA’ situation, and be careful! Make a conjecture about the number of triangles determined by the SSA information.
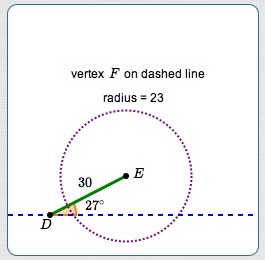
Looks like a two triangle situation!
It's also useful to use a table (or tables) to organize results:
| Angle | Opposite Side |
| $\, D = 27^\circ$ | $d = 23$ |
| $\, E = \,?$ | $\,e = \,?$ |
| $\, F = \,?$ | $\,f = 30$ |
The table(s) will be filled in as computations are completed.
In this example, the tables are repeated, so you can easily see each step where information is added. When doing problems like this on your own, you won't repeat the table(s)—you'll just fill them in as you go.
Use the Law of Sines:
$$ \begin{gather} \cssId{s121}{\frac{\sin 27^\circ}{23} = \frac{\sin F}{30}}\cr\cr \cssId{s122}{\sin F = \frac{30}{23}\sin 27^\circ \approx 0.5922} \end{gather} $$Find both angles (between $\,0^\circ\,$ and $\,180^\circ\,$) that have a sine of $\,0.5922\,$:
$$ \begin{gather} \cssId{s124}{\arcsin(0.5922) \approx \color{red}{36.3^\circ}}\cr\cr \cssId{s125}{180^\circ - 36.3^\circ = \color{red}{143.7^\circ}} \end{gather} $$Note:
- If your calculator is in radian mode, then $\,\arcsin(0.5922)\,$ is reported in radians.
- If your calculator is in degree mode, then $\,\arcsin(0.5922)\,$ is reported in degrees.
- WolframAlpha reports both radians and degrees.
Add this information to the tables (one table for each triangle):
| Angle | Opposite Side |
| $D = 27^\circ$ | $d = 23$ |
| $E = \,?$ | $e = \,?$ |
| $F = \color{red}{36.3^\circ}$ | $\,f = 30$ |
| Angle | Opposite Side |
| $D = 27^\circ$ | $d = 23$ |
| $E = \,?$ | $e = \,?$ |
| $F = \color{red}{143.7^\circ}$ | $\,f = 30$ |
Compute the remaining angles:
$$ \begin{gather} \cssId{s134}{180^\circ - 27^\circ - 36.3^\circ = \color{red}{116.7^\circ}}\cr\cr \cssId{s135}{180^\circ - 27^\circ - 143.7^\circ = \color{red}{9.3^\circ}}\cr\cr \end{gather} $$Add this information to the tables:
| Angle | Opposite Side |
| $D = 27^\circ$ | $d = 23$ |
| $E = \color{red}{116.7^\circ}$ | $e = \,?$ |
| $F = 36.3^\circ$ | $f = 30$ |
| Angle | Opposite Side |
| $D = 27^\circ$ | $d = 23$ |
| $E = \color{red}{9.3^\circ}$ | $e = \,?$ |
| $F = 143.7^\circ$ | $f = 30$ |
Use the Law of Sines again to compute the remaining side:
$$ \begin{gather} \cssId{s140}{\frac{\sin 27^\circ}{23} = \frac{\sin 116.7^\circ}{e}}\cr\cr \cssId{s141}{e = \frac{23\sin 116.7^\circ}{\sin 27^\circ} \approx \color{red}{45.26}}\cr\cr\cr \cssId{s142}{\frac{\sin 27^\circ}{23} = \frac{\sin 9.3^\circ}{e}}\cr\cr \cssId{s143}{e = \frac{23\sin 9.3^\circ}{\sin 27^\circ} \approx \color{red}{8.19}} \end{gather} $$Add this information to the tables:
| Angle | Opposite Side |
| $D = 27^\circ$ | $d = 23$ |
| $E = 116.7^\circ$ | $e = \color{red}{45.26}$ |
| $F = 36.3^\circ$ | $f = 30$ |
| Angle | Opposite Side |
| $D = 27^\circ$ | $d = 23$ |
| $E = 9.3^\circ$ | $e = \color{red}{8.19}$ |
| $F = 143.7^\circ$ | $f = 30$ |
Check your results by making sure the ratios in the Law of Sines are all the same:
$$ \begin{gather} \cssId{s148}{\frac{\sin 27^\circ}{23} = \frac{\sin 116.7^\circ}{45.26} = \frac{\sin 36.3^\circ}{30} = 0.0197}\cr \cssId{s149}{\text{Check!}}\cr\cr\cr \cssId{s150}{\frac{\sin 27^\circ}{23} = \frac{\sin 9.3^\circ}{8.19} = \frac{\sin 143.7^\circ}{30} = 0.0197}\cr \cssId{s151}{\text{Check!}} \end{gather} $$You can use WolframAlpha to do the computations. For example, you can type:
23 sin(116.7 deg) / sin(27 deg)
to compute:
$$ \cssId{s156}{\frac{23\sin 116.7^\circ}{\sin 27^\circ}} $$