audio read-through Basic Function Models You Must Know (Part 2)

(This page is Part 2. Click here for Part 1.)

Exponential Functions

the natural exponential function
$f(x) = {\text{e}}^x$
or
$f(x) = \exp(x)$

other bases:
$y = 2^x$
$y = 3^x$
$y = (\frac{1}{2})^x$

detail

There is an entire family of exponential functions. They are of the form $\,y = b^x\,,$ where $\,b\,$ is a positive number, not equal to $\,1\,.$

For example, $\,y = 2^x\,$ and $\,y = (1/2)^x\,$ are exponential functions. Thus, exponential functions have a constant base; the variable is in the exponent.

Of all the exponential functions, $\,f(x) = {\text{e}}^x\,$ (base $\,\text{e}\,$) is singled out as most important, due to the simplicity of a calculus property it possesses:

The slope of the tangent line at the point $\,(x,{\text{e}}^x)\,$ is $\,m = {\text{e}}^x\,.$ That is, the $y$-value of the point gives the slope of the tangent line.

Think about this! If $\,y = 100\,,$ then the slope of the tangent line there is $\,100\,,$ so the $y$-values are increasing $\,100\,$ times faster than the inputs! (Exponential functions with other bases have a similar, but not-so-simple property.)

Increasing exponential functions get big FAST!

$f(x) = {\text{e}}^x\,$ is given the special name ‘the natural exponential function’ and is also denoted by $\,f(x) = \exp(x)\,.$

Recall that $\,\text{e}\,$ is defined as the number that $\,(1 + \frac 1n)^n\,$ approaches as $n\rightarrow\infty\,$; $\,\text{e}\,$ is irrational; $\,\text{e}\approx 2.71828\,.$

If you hear the phrase ‘the exponential function’ (meaning only one) then the function being referred to is the natural exponential function.

Properties That ALL Exponential Functions Share

Properties Dependent on the Base

  base greater than $\,1\,$ base between $\,0\,$ and $\,1\,$
end behavior as $\,x \rightarrow \infty\,,$ $\,y\rightarrow \infty$

as $\,x \rightarrow -\infty\,,$ $\,y\rightarrow 0$ 		as $\,x \rightarrow \infty\,,$ $\,y\rightarrow 0$

as $\,x \rightarrow -\infty\,,$ $\,y\rightarrow \infty$
increasing/decreasing increases everywhere decreases everywhere

Logarithmic Functions

the natural logarithm function
$f(x) = \ln(x)$

other bases:
$y = \log_2(x)$
$y = \log_3(x)$
$y = \log_{1/2}(x)$

detail

There is an entire family of logarithmic functions. They are of the form $\,y = \log_b(x)\,,$ where $\,b\,$ is a positive number, not equal to $\,1\,.$

For example, $\,y = \log_2(x)\,$ and $\,y = \log_{1/2}(x)\,$ are logarithmic functions.

When the base is the irrational number $\,\text{e}\,,$ the function is given a special name: $\,f(x) = \ln(x) := \log_{\text{e}}(x)\,.$

Of all the logarithmic functions, $\,f(x) = \ln(x)\,$ is singled out as most important, due to the simplicity of a calculus property it possesses:

The slope of the tangent line at the point $\,(x,\ln x)\,$ is $\,m = \frac 1x\,.$ That is, the reciprocal of the $x$-value of the point gives the slope of the tangent line.

Think about this! If $x = 100\,,$ then the slope of the tangent line there is only $\,\frac{1}{100}\,,$ so the $y$-values are increasing only $\,\frac{1}{100}\,$ times as fast as the inputs! (Logarithmic functions with other bases have a similar, but not-so-simple property.)

Increasing logarithmic functions get big, but they get big VERY SLOWLY!

$f(x) = \ln(x)\,$ is given the special name ‘the natural logarithm function’.

Recall that $\,\text{e}\,$ is defined as the number that $\,(1 + \frac 1n)^n\,$ approaches as $n\rightarrow\infty\,$; $\,\text{e}\,$ is irrational; $\,\text{e}\approx 2.71828\,.$

Some disciplines use $\,\log(x)\,$ (no indicated base) to mean the natural logarithm. Some disciplines use $\,\log(x)\,$ to mean the common logarithm (base ten). You'll need to check notation.

Properties That ALL Logarithmic Functions Share

Properties Dependent on the Base

  base greater than $\,1\,$ base between $\,0\,$ and $\,1\,$
end behavior as $\,x \rightarrow \infty\,,$ $\,y\rightarrow \infty$
 as $\,x \rightarrow \infty\,,$ $\,y\rightarrow -\infty$
behavior near zero as $\,x \rightarrow 0^+\,,$ $\,y\rightarrow -\infty$
 as $\,x \rightarrow 0^+\,,$ $\,y\rightarrow \infty$
increasing/decreasing increases on its domain decreases on its domain

The Sine and Cosine Functions

defining sine and cosine on the unit circle

the sine function
$f(x) = \sin(x)$

the cosine function
$f(x) = \cos(x)$

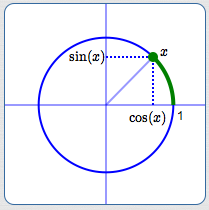
The sine function gives the $y$-values of points on the unit circle.

The cosine function gives the $x$-values of points on the unit circle.

(See the discussion below to understand how to associate real numbers, $\,x\,,$ with points on the unit circle.)

Both sine and cosine share the following properties:

Associating Real Numbers With Points on the Unit Circle

Start with a circle centered at the origin with radius $\,1\,,$ as shown below. Sine and cosine are both defined using this unit circle; the other trigonometric functions are defined in terms of sine and cosine.

associating a real number with a point on the unit circle
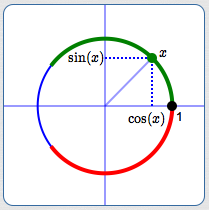
associating real numbers with points on the unit circle

We must associate the real numbers with points on this unit circle. To do this, think of the real number line as an infinite string:

Pick up this piece of string and wrap it around the circle as follows:

Of course, the green and red will overlap, as they continue to wrap around and around the circle. (Only a short piece of green and red ‘string’ are shown here!)

In this way:

So, when you think about sine and cosine (and the other trigonometric functions) acting on a real number $\,x\,,$ you want to think of $\,x\,$ in this way!

The Tangent Function

the tangent function
$f(x) = \tan(x)$

The tangent function is defined as:

$$\cssId{s119}{\tan(x) := \frac{\sin(x)}{\cos(x)}}$$

Concept Practice