Graphical Interpretation of Sentences like $f(x)=g(x)$ and $f(x)>g(x)$

Need some basic information on graphs of functions and related concepts first?  Graphs of Functions

This section should feel remarkably similar to the previous one: Graphical interpretation of sentences like $\,f(x) = 0\,$ and $\,f(x) \gt 0\,.$ This current section is more general—to return to the previous ideas, just let $\,g(x)\,$ be the zero function.

If you know the graphs of two functions $\,f\,$ and $\,g\,,$ then it is very easy to visualize the solution sets of sentences like $\,f(x) = g(x)\,$ and $\,f(x)\gt g(x)\,.$ This section shows you how!

A key observation is that a sentence like $\,f(x) = g(x)\,$ or $\,f(x) \gt g(x)\,$ is a sentence in one variable, $\,x\,.$ To solve such a sentence, you are looking for value(s) of $\,x\,$ that make the sentence true. The functions $\,f\,$ and $\,g\,$ are known, and determine the graphs that you'll be investigating.

Recall that the graph of a function $\,f\,$ is a picture of all points of the form $\,(x,f(x))\,,$ and the graph of a function $\,g\,$ is a picture of all points of the form $\,(x,g(x))\,.$

In particular, the $\,y$-value of the point $\,(x,f(x))\,$ is the number $\,f(x)\,$ and the $\,y$-value of the point $\,(x,g(x))\,$ is the number $\,g(x)\,$:

• If $\,f(x)\gt g(x)\,,$ then the point $\,(x,f(x))\,$ lies above the point $\,(x,g(x))\,.$
• If $\,f(x)=g(x)\,,$ then the graphs of $\,f\,$ and $\,g\,$ intersect at this point.
• If $\,f(x)\lt g(x)\,,$ then the point $\,(x,f(x))\,$ lies below the point $\,(x,g(x))\,.$

These concepts are illustrated below.

The notation
$\,P(x,f(x))\,$
is a convenient shorthand for:
the point $\,P\,$ with coordinates $\,(x,f(x))$

$P_1(x,f(x))\,$ and $\,P_2(x,g(x))\,$
with $\,f(x)\gt g(x)\,$

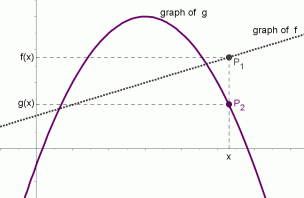
for this value of $\,x\,,$
the graph of $\,f\,$ lies above the graph of $\,g$

$P_1(x,f(x))\,$ and $\,P_2(x,g(x))\,$
with $\,f(x)=g(x)$

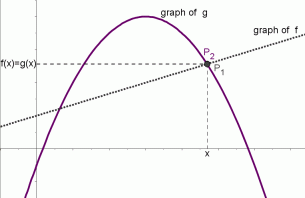
for this value of $\,x\,,$
the graphs of $\,f\,$ and $\,g\,$ intersect

$P_1(x,f(x))\,$ and $P_2(x,g(x))\,$
with $\,f(x)\lt g(x)$

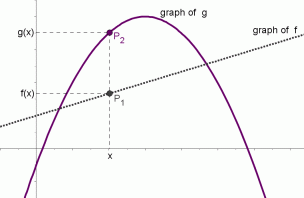
for this value of $\,x\,,$
the graph of $\,f\,$ lies below the graph of $\,g$

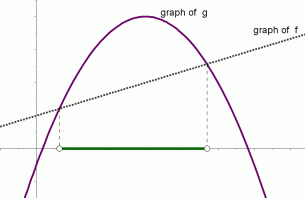
The graphs of functions $\,f\,$ and $\,g\,$ are shown below. The solution set of the inequality ‘$\,f(x)\gt g(x)\,$’ is shown in green. It is the set of all values of $\,x\,$ for which the graph of $\,f\,$ lies above the graph of $\,g\,.$

The graphs of functions $\,f\,$and $\,g\,$ are shown below. The solution set of the equation ‘$\,f(x)=g(x)\,$’ is shown in green. It is the set of all values of $\,x\,$ for which the graphs of $\,f\,$ and $\,g\,$ intersect.

The graphs of functions $\,f\,$ and $\,g\,$ are shown below. The solution set of the inequality ‘$\,f(x)\lt g(x)\,$’ is shown in green. It is the set of all values of $\,x\,$ for which the graph of $\,f\,$ lies below the graph of $\,g\,.$

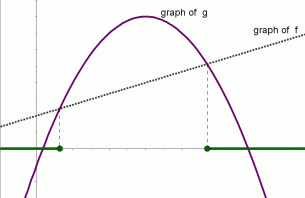
The graphs of functions $\,f\,$ and $\,g\,$ are shown below. The solution set of the inequality ‘$\,f(x)\ge g(x)\,$’ is shown in green. It is the set of all values of $\,x\,$ for which the graph of $\,f\,$ lies on or above the graph of $\,g\,.$

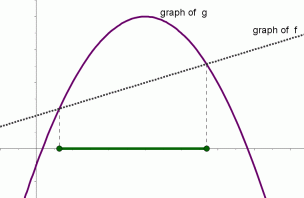
The graphs of functions $\,f\,$ and $\,g\,$ are shown below. The solution set of the inequality ‘$\,f(x)\le g(x)\,$’ is shown in green. It is the set of all values of $\,x\,$ for which the graph of $\,f\,$ lies on or below the graph of $\,g\,.$

Example

The graphs of two functions, each with domain $\,\mathbb{R}\,,$ are shown below:

• $\,f\,$ is a parabola, shown in the black dotted pattern;
• $\,g\,$ is a cubic polynomial, shown in purple.

These two curves intersect at the points $\,(-1,2)\,,$ $\,(0,0.5)\,$ and $\,(1,1)\,.$

Pay attention to the difference between the brackets ‘$\,[\ ]\,$’ and parentheses ‘$\,(\ )\,$’ and braces ‘$\,\{\ \}\,$’ in the solutions sets!

Remember that the symbol ‘$\,\cup\,$’, the union symbol, is used to put sets together.

The solution set of the inequality ‘$\,f(x)\gt g(x)\,$’ is: $$\cssId{s66}{(-\infty ,-1) \cup (0,1)}$$

The solution set of the equation ‘$\,f(x)=g(x)\,$’ is: $$\cssId{s68}{\{-1,0,1\}}$$

The solution set of the inequality ‘$\,f(x)\lt g(x)\,$’ is: $$\cssId{s70}{(-1,0)\cup (1,\infty)}$$

The solution set of the inequality ‘$\,f(x)\ge g(x)\,$’ is: $$\cssId{s72}{(-\infty ,-1] \cup [0,1]}$$

The solution set of the inequality ‘$\,f(x)\le g(x)\,$’ is: $$\cssId{s74}{[-1,0] \cup [1,\infty )}$$

Let's discuss the solution set of the inequality ‘$\,f(x)\gt g(x)\,$’.

Imagine a vertical line passing through the graph, moving from left to right. Every time the vertical line is at a place where the graph of $\,f\,$ lies above the graph of $\,g\,,$ then you must include that $\,x$-value in the solution set.

Be extra careful of places where something interesting is happening (like where the graphs intersect).