Graphical Interpretation of Sentences like $\,f(x)=0\,$ and $\,f(x)\gt 0$
Need some basic information on graphs of functions first? Graphs of Functions
If you know the graph of a function $\,f\,,$ then it is very easy to visualize the solution sets of sentences like $\,f(x)=0\,$ and $\,f(x)\gt 0\,.$ This section shows you how!
A key observation is that a sentence like $\,f(x) = 0\,$ or $\,f(x) \gt 0\,$ is a sentence in one variable, $\,x\,.$ To solve such a sentence, you are looking for value(s) of $\,x\,$ that make the sentence true. The function $\,f\,$ is known, and determines the graph that you'll be investigating.
Recall that the graph of a function $\,f\,$ is a picture of all its (input,output) pairs: that is, it is a picture of all points of the form $\,(x,f(x))\,.$
In particular, the $\,y$-value of the point $\,(x,f(x))\,$ is the number $\,f(x)\,$:
- If $\,f(x)\gt 0\,,$ then the point $\,(x,f(x))\,$ lies above the $\,x$-axis.
- If $\,f(x)=0\,,$ then the point $\,(x,f(x))\,$ lies on the $\,x$-axis.
- If $\,f(x)\lt 0\,,$ then the point $\,(x,f(x))\,$ lies below the $\,x$-axis.
These concepts are illustrated below.
The notation
$\,P(x,f(x))\,$
is a convenient shorthand for:
the point $\,P\,$ with coordinates
$\,(x,f(x))$
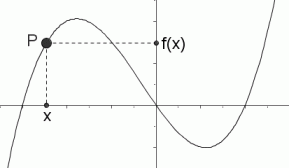
point $\,P(x,f(x))\,$ has $\,f(x)\gt 0\,$
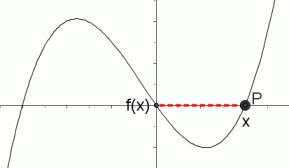
point $\,P(x,f(x))\,$ has $\,f(x)=0\,$
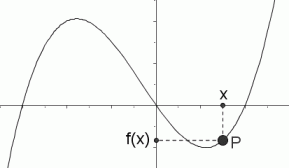
point$\, P(x,f(x))\,$ has $\,f(x)\lt 0\,$
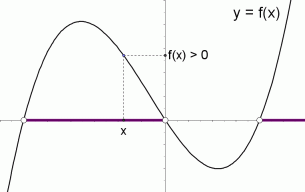
The graph of a function $\,f\,$ is shown below. The solution set of the inequality ‘$\,f(x)\gt 0\,$’ is shown in purple. It is the set of all values of $\,x\,$ for which $\,f(x)\,$ is positive. That is, it is the set of $\,x$-values that correspond to the part of the graph above the $\,x$-axis.
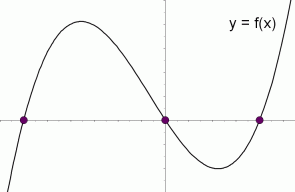
The graph of a function $\,f\,$ is shown below. The solution set of the equation ‘$\,f(x)=0\,$’ is shown in purple. It is the set of all values of $\,x\,$ for which $\,f(x)\,$ equals zero. That is, it is the set of $\,x$-intercepts of the graph.
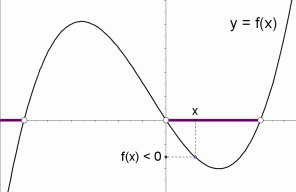
The graph of a function $\,f\,$ is shown below. The solution set of the inequality ‘$\,f(x)\lt 0\,$’ is shown in purple. It is the set of all values of $\,x\,$ for which $\,f(x)\,$ is negative. That is, it is the set of $\,x$-values that correspond to the part of the graph below the $\,x$-axis.
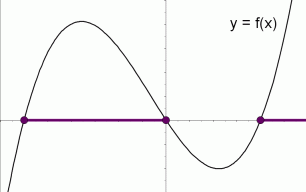
The graph of a function $\,f\,$ is shown below. The solution set of the inequality ‘$\,f(x)\ge 0\,$’ is shown in purple. It is the set of all values of $\,x\,$ for which $\,f(x)\,$ is nonnegative. That is, it is the set of $\,x$-values that correspond to the part of the graph that is either on or above the $\,x$-axis.
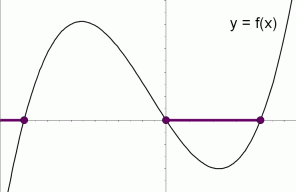
The graph of a function $\,f\,$ is shown below. The solution set of the inequality ‘$\,f(x)\le 0\,$’ is shown in purple. It is the set of all values of $\,x\,$ for which $\,f(x)\,$ is nonpositive. That is, it is the set of $\,x$-values that correspond to the part of the graph that is either on or below the $\,x$-axis.
My sister and I have finished our house-clean-out adventure! Here are photos of the house (30 Mt Laurel Way, Monterey, MA). Click on any photo for captions. It should be on the MLS soon.
Want to say hello? Sign my guestbook!
Example
The graph of a function $\,g\,$ with domain $\,[-6,10)\,$ is shown below.
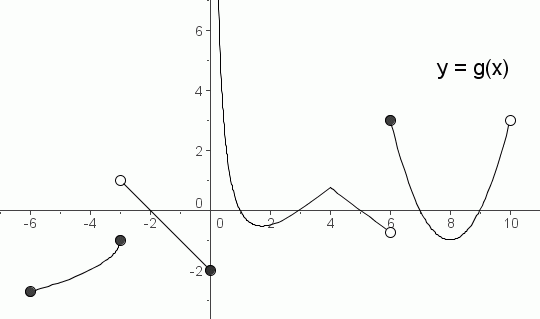
Pay attention to the difference between the brackets ‘$\,[\ ]\,$’ and parentheses ‘$\,(\ )\,$’ and braces ‘$\,\{\ \}\,$’ in the solutions sets!
The solution set of the inequality ‘$\,g(x)\gt 0\,$’ is: $$\cssId{s41}{(-3,-2)\cup (0,1)\cup (3,5)\cup [6,7)\cup (9,10)}$$
The solution set of the inequality ‘$\,g(x)\ge 0\,$’ is: $$\cssId{s43}{(-3,-2]\cup (0,1]\cup[3,5]\cup[6,7]\cup[9,10)}$$
The solution set of the equation ‘$\,g(x)=0\,$’ is: $$\cssId{s45}{\{-2,1,3,5,7,9\}}$$
The solution set of the inequality ‘$\,g(x)\lt 0\,$’ is: $$\cssId{s47}{[-6,-3]\cup (-2,0]\cup (1,3)\cup (5,6)\cup (7,9)}$$
The solution set of the inequality ‘$\,g(x)\le 0\,$’ is: $$\cssId{s49}{[-6,-3]\cup [-2,0]\cup [1,3]\cup [5,6)\cup [7,9]}$$
Let's discuss the solution set of the inequality ‘$\,g(x)\gt 0\,$’.
Imagine a vertical line passing through the graph, moving from left to right. Every time the vertical line touches a point that lies above the $\,x$-axis, then you must include that $\,x$-value in the solution set.
Be extra careful of ‘boundary’ or ‘transition’ points—places where something interesting is happening (like where the graph crosses the $\,x$-axis, or where there's a break in the graph).
For example, suppose the vertical line reaches $\,x = -3\,.$ The point (the filled-in circle) is below the $\,x$-axis, so we don't want this $\,x$-value.
But then, the graph is above until we reach $\,x = -2\,.$ When $\,x = -2\,,$ the point is on the $\,x$-axis, so we don't want this $\,x$-value, either.
This discussion gives the interval $\,(-3,-2)\,$ in the solution set.
Remember that the symbol ‘$\,\cup\,$’, the union symbol, is used to put sets together.
Graphical Interpretation of Sentences like $\,f(x)=g(x)\,$ and $\,f(x)\gt g(x)$
Concept Practice
- Choose a specific problem type, or click ‘New problem’ for a random question.
- Think about your answer.
- Click ‘Check your answer’ to check!