Appendix 2: Vector Spaces, Norms and Inner Products
A mathematical object called a vector space provides the structure necessary to discuss linear combinations of elements, such as:
$$ a_1x_1 + a_2x_2 + \cdots + a_nx_n $$A vector space consists of a set of objects, called vectors, on which two operations are defined: addition, and multiplication by scalars. The precise definition follows:
Let $\,V\,$ be a set of objects, and let $\,\Bbb F\,$ denote either the real numbers ($\,\Bbb R\,$) or the complex numbers ($\,\Bbb C\,$). The elements of $\,\Bbb F\,$ are called scalars.
Let $\,+\,$ and $\,\cdot\,$ denote operations:
$$ \begin{align} +\ &:\,V\times V\rightarrow V\ ,\ \ (x,y)\mapsto x+y\cr \cdot\,\ &:\,F\times V\rightarrow V\ ,\ \ (\alpha,y)\mapsto \alpha\cdot x \end{align} $$The operation ‘$\,+\,$’ is called addition, and ‘$\,\cdot\,$’ is called scalar multiplication. The element $\,\alpha\cdot x\,$ is denoted more simply by $\,\alpha x\,.$
Observe that $\,x+y\,$ and $\,\alpha x\,$ must be in $\,V\,,$ for all $\,x,y\in V\,$ and $\,\alpha\in\Bbb F\,$; that is, $\,V\,$ is closed under addition and scalar multiplication.
If the axioms listed below are satisfied for all $\,x\,,$ $\,y\,$ and $\,z\,$ in $\,V\,,$ and for all scalars $\,\alpha\,$ and $\,\beta\,,$ then $\,V\,$ is called a vector space over $\,\Bbb F\,,$ and the elements of $\,V\,$ are called vectors:
- addition is commutative: $\,x + y = y + x$
- addition is associative: $x + (y + z) = (x + y) + z$
- zero vector: There exists a vector $\,0\in V\,,$ called the zero vector, satisfying $\,x + 0 = x\,$ for all $\,x\in V\,.$
- additive inverses: For every $\,x\in V\,$ there exists a vector $\,-x\in V\,$ satisfying $\,x + (-x) = 0\,.$ The vector $\,-x\,$ is called the additive inverse of $\,x\,.$
- distributive laws: $\,\alpha(x + y) = \alpha x + \alpha y\,,$ and $\,(\alpha + \beta)x = \alpha x + \beta x$
- $\,1x = x\,,$ and $\,\alpha(\beta x) = (\alpha\beta)x$
Vector spaces in which the scalars are real numbers are called real vector spaces, and those in which the scalars are complex numbers are complex vector spaces.
Uniqueness of the zero vector and additive inverses follows readily from the definition. The name $\,-x\,$ is justified for the additive inverse, since it can be easily shown that $\,(-1)\cdot x = -x\,.$ The symbol $\,0\,$ is used to denote both $\,0\in\Bbb F\,$ and $\,0\in V\,,$ with context determining the proper interpretation.
Primarily real vector spaces are considered in this appendix.
Let $\,\Bbb R^n\,$ be the set of all ordered $n$-tuples of real numbers:
$$ \Bbb R^n := \{(x_1,\ldots,x_n)\,:\, x_i\in\Bbb R\,,\ \ 1\le i\le n\} $$For $\,x = (x_1,\ldots,x_n)\,$ and $\,y = (y_1,\ldots,y_n)\,$ in $\,\Bbb R^n\,,$ and $\,\alpha\in\Bbb R\,,$ define addition and scalar multiplication by:
$$ \begin{align} (x_1,\ldots,x_n) + (y_1,\ldots,y_n) &:= (x_1+y_1,\ldots,x_n+y_n)\cr\cr \alpha(x_1,\ldots,x_n) &:= (\alpha x_1,\ldots,\alpha x_n) \end{align} $$The set $\,\Bbb R^n\,,$ together with these operations, is a real vector space. This space, together with the usual measure of distance between elements, given by
$$ d(x,y) = \sqrt{(x_1-y_1)^2 + \cdots + (x_n-y_n)^2}\ , $$is called $n$-dimensional Euclidean space.
The set of all $\,n \times m\,$ matrices with real number entries, together with the usual definitions of matrix addition and multiplication by real numbers, forms a real vector space which is denoted by $\,\Bbb R^{n\times m}\,.$ The zero vector in $\,\Bbb R^{n\times m}\,$ is the $\,n \times m\,$ zero matrix. The additive inverse of $\,X\in\Bbb R^{n\times m}\,$ is found by multiplying each entry of $\,X\,$ by the scalar $\,-1\,.$
In addition to providing foundational material for review, the definitions and theorems that follow are needed to discuss the existence and uniqueness of solutions to the linear least-squares problem.
Let $\,V\,$ be a vector space over $\,\Bbb F\,,$ and let $\,y\in V\,.$ Then, $\,y\,$ is said to be a linear combination of vectors $\,x_1,\ldots,x_n\,$ in $\,V\,$ provided there exist scalars $\,\alpha_1,\ldots,\alpha_n\,$ in $\,\Bbb F\,$ for which:
$$ y = \alpha_1 x_1 + \cdots + \alpha_n x_n $$Let $\,V\,$ be a vector space over $\,\Bbb F\,.$ A subset $\,W \subseteq V\,$ is called a subspace of $\,V\,$ if $\,W\,$ is itself a vector space over $\,\Bbb F\,,$ with the same operations of addition and scalar multiplication used in $\,V\,.$ In particular, $\,W\,$ must be closed under addition and scalar multiplication.
Let $\,V\,$ be a vector space, and let $\,S\,$ be a nonempty subset of $\,V\,.$ The subspace spanned by $\,S\,$ is the intersection of all subspaces of $\,V\,$ that contain $\,S\,.$ If $\,M\,$ is the subspace spanned by $\,S\,,$ then the vectors in $\,S\,$ are said to span $\,M\,.$
Thus, the subspace spanned by $\,S\,$ is the ‘smallest’ subspace of $\,V\,$ that contains $\,S\,.$ It can be shown [H&K, p. $37$] that the subspace spanned by $\,S\,$ consists of all linear combinations of the elements from $\,S\,.$
A subset $\,C\,$ of a vector space $\,V\,$ is said to be convex if whenever $\,x,y \in C\,,$ then also:
$$ M := \{\alpha x + (1-\alpha)y\ |\ 0\le\alpha\le 1\} \subseteq C $$In $\,\Bbb R\,,$ $\,\Bbb R^2\,$ and $\,\Bbb R^3\,,$ the set $\,M\,$ of the previous definition is the line segment connecting $\,x\,$ and $\,y\,.$
It is routine to verify that subspaces are convex.
Let $\,V\,$ be a vector space over $\,\Bbb F\,.$ A nonempty subset $\,S\subseteq V\,$ is said to be linearly independent if it has the following property: whenever a finite collection $\,x_1,\ldots,x_n\,$ of distinct vectors from $\,S\,$ satisfies
$$ \alpha_1x_1 + \cdots + \alpha_nx_n = 0 $$for scalars $\,\alpha_1,\ldots,\alpha_n\,,$ then it must be that:
$$ \alpha_1 = \alpha_2 = \cdots = \alpha_n = 0 $$Consequently, if $\,S\,$ is not linearly independent, then there exist distinct vectors $\,x_1,\ldots,x_n\,$ in $\,S\,,$ and scalars $\,\alpha_1,\ldots,\alpha_n\,,$ not all zero, for which:
$$ \alpha_1x_1 + \cdots + \alpha_nx_n = 0 $$In this case, $\,S\,$ is said to be linearly dependent.
Let $\,V\,$ be a vector space. A basis for $\,V\,$ is a linearly independent set of vectors from $\,V\,$ that spans $\,V\,.$ If $\,V\,$ has a finite basis, then it is finite-dimensional. The notation $\,\text{dim}(V) = n\,$ is used to denote that $\,V\,$ has dimension $\,n\,.$
It can be shown that any two bases for a finite-dimensional vector space have the same number of vectors [Anton, p. $162$].
Let $\,V\,$ and $\,W\,$ be vectors spaces over $\,\Bbb F\,.$ In what follows, the notation ‘$+$’ is used to denote both the addition in $\,V\,,$ and the addition in $\,W\,.$
A linear transformation from $\,V\,$ into $\,W\,$ is a function $\,T\,:\,V\rightarrow W\,$ satisfying, for all $\,x, y \in V\,$ and for all $\,\alpha\in\Bbb F\,$:
$$ \begin{align} T(x+y) &= T(x) + T(y)\cr &\text{and}\cr T(\alpha x) &= \alpha T(x) \end{align} $$The set $\,\{ x\in V\ |\ T(x) = 0\}\,$ is called the kernel of $\,T\,$ and denoted by $\,\text{ker}(T)\,.$
The set
$$ \{w\in W\,|\, \text{there exists } v\in V\text{ with } T(v) = w\} $$is called the range of $\,T\,,$ and is denoted by $\,{\cal R}(T)\,.$
Let $\,V\,$ and $\,W\,$ be vectors spaces over $\,\Bbb F\,,$ and let $\,T\,:\, V \rightarrow W\,$ be a linear transformation.
The set $\,\text{ker}(T)\,$ is a subspace of $\,V\,,$ and the set $\,{\cal R}(T)\,$ is a subspace of $\,W\,$ [Anton, p. $231$].
If $\,V\,$ has dimension $\,n\,,$ then ([Anton, p. $233$]):
$$ \text{dim}\bigl({\cal R}(T)\bigr) + \text{dim}\bigl(\text{ker}(T)\bigr) = n $$Let $\,M\,$ be an $\,n \times m\,$ matrix with real entries. The matrix $\,M\,$ naturally defines a linear transformation from $\,\Bbb R^m\,$ to $\,\Bbb R^n\,,$ as follows: let $\,x\in \Bbb R^m\,$ be represented by an $\,m \times 1\,$ vector. Then, $\,Mx\,$ is an $\,n \times 1\,$ vector, so $\,Mx \in \Bbb R^n\,.$ It is routine to verify that this map
$$ x\overset{M}{\mapsto} Mx $$satisfies the requirements of a linear transformation. Let $\,M\,$ denote both the matrix $\,M\,,$ and the linear transformation defined by $\,M\,,$ with context determining the correct interpretation.
By the previous theorem, the range of $\,M\,$ is a subspace of $\,\Bbb R^n\,$; the dimension of the range is called the rank of $\,M\,.$ Each column of $\,M\,$ is a vector in $\,\Bbb R^n\,.$ It can be shown that the range of $\,M\,$ is the subspace of $\,\Bbb R^n\,$ spanned by the column vectors of $\,M\,.$
The kernel of $\,M\,$ is the set
$$ \text{ker}(M) = \{x\in\Bbb R^m\ |\ Mx = 0\}\ , $$where, here, $\,0\,$ denotes the $\,n \times 1\,$ zero vector.
If the number of rows in $\,M\,$ is the same as the number of columns, then $\,M\,$ is called a square matrix. By definition, $\,M\,$ is invertible if and only if there exists a matrix $\,M^{-1}\,$ satisfying $\,MM^{-1} = M^{-1}M = I\,.$ There are many equivalent characterizations of invertibility:
[Anton, p. $171$] If $\,M\,$ is an $\,n \times n\,$ matrix, then the following statements are equivalent:
- $M\,$ is invertible.
- $\text{ker}(M) = \{0\}$
- The determinant of $\,M\,$ is nonzero.
- $M\,$ has rank $\,n\,.$
- The row vectors of $\,M\,$ are linearly independent.
- The column vectors of $\,M\,$ are linearly independent.
A vector space $\,V\,$ serves as the starting point for other useful spaces. If $\,V\,$ is endowed with additional structure that allows one to measure the ‘size’ of elements of $\,V\,,$ then $\,V\,$ is called a normed space. The precise definition follows:
Let $\,V\,$ be a vector space over $\,\Bbb F\,,$ and let $\,\alpha\in\Bbb F\,.$
If $\,\Bbb F = \Bbb R\,,$ then $\,|\alpha|\,$ denotes the absolute value of $\,\alpha\,.$ If $\,\Bbb F = \Bbb C\,,$ then for $\,\alpha = a + bi\,,$ $\,|\alpha| = \sqrt{a^2 + b^2}\,.$
A norm on $\,V\,$ is a function,
$$ \|\ \|\,:\, V\rightarrow \Bbb R\,,\ \ x\mapsto \|x\|\ , $$that assigns to each $x\in V\,$ a nonnegative real number $\,\|x\|\,,$ and that satisfies the following additional properties, for all $\,x\in V\,$ and $\,\alpha\in\Bbb F\,$:
- $\|x\| = 0\iff x = 0$
- $\|\alpha x\| = |\alpha|\cdot \|x\|$
- triangle inequality: $\,\|x + y\| \le \|x\| + \|y\|$
A vector space $\,V\,,$ together with a norm on $\,V\,,$ is called a normed space.
In a normed space, the distance between vectors $\,x\,$ and $\,y\,$ can be defined via:
$$ d(x,y) := \|x-y\| $$It is routine to verify that the distance function defined in this way satisfies the properties given in the next definition:
Let $\,S\,$ be a set. A function
$$ d\,:\,S\times S \rightarrow [0,\infty)\,,\ \ (x,y) \mapsto d(x,y)\ , $$is called a metric on $\,S\,,$ if it satisfies the following properties:
- $d(x,y) = 0\iff x = y$
- symmetry: $\,d(x,y) = d(y,x)$
- triangle inequality: $\,d(x,y) \le d(x,z) + d(z,y)$
A set $\,S\,,$ together with a metric on $\,S\,,$ is called a metric space.
Consequently, every normed space is a metric space. Observe that a metric space need not be a vector space ($\bigstar\,$ just as a topological space need not be a vector space). However, many interesting metric spaces are also vector spaces.
Let $\,S\,$ be a metric space, with metric $\,d\,.$
Let $\,(x_n)_{n=1}^\infty\,$ be a sequence in $\,S\,,$ and let $\,x\in S\,.$ The sequence $\,(x_n)_{n=1}^\infty\,$ is said to converge to $\,x\,$ if for every $\,\epsilon \gt 0\,,$ there exists a positive integer $\,N = N(\epsilon)\,,$ such that for all $\,n \gt N\,,$ $\,d(x_n,x) \lt \epsilon\,.$
A sequence $\,(x_n)_{n=1}^\infty\,$ from $\,S\,$ is said to be Cauchy (pronounced ‘KO-shee’) if for every $\,\epsilon \gt 0\,,$ there exists a positive integer $\,N = N(\epsilon)\,,$ such that if $\,m, n \gt N\,,$ then $\,d(x_m,x_n) \lt \epsilon\,.$
The space $\,S\,$ is said to be complete if whenever $\,(x_n)_{n=1}^\infty\,$ is a Cauchy sequence in $\,S\,,$ then there exists $\,x\in S\,$ such that the sequence $\,(x_n)\,$ converges to $\,x\,.$
Every finite-dimensional subspace of a normed space is complete (in the metric induced by the norm) [Krey, p. $73$].
If a vector space $\,V\,$ is endowed with structure which enables one to talk about angles between vectors, and in particular orthogonality (perpendicularity) of vectors, then it is called an inner product space. Only real vector spaces are treated in the next definition:
Let $\,V\,$ be a real vector space.
An inner product on $\,V\,$ is a function,
$$ \langle\ ,\,\rangle\ :\ V\times V \rightarrow \Bbb R\ ,\ \ (x,y) \mapsto \langle x,y\rangle\ , $$that satisfies the following properties, for all $\,x,y,z\in V\,$ and for all $\,\alpha\in\Bbb R\,$:
- $\langle x+y,z\rangle = \langle x,z\rangle + \langle y,z\rangle$
- $\langle \alpha x,y\rangle = \alpha\langle x,y\rangle$
- $\langle x,y\rangle = \langle y,x\rangle$
- $\langle x,x\rangle\,$ is a nonnegative real number
- $\langle x,x\rangle = 0\iff x = 0$
A vector space $\,V\,$ with an inner product on $\,V\,$ is called an inner product space.
It follows easily from the definition that, for all $\,\alpha\in\Bbb R\,$ and $\,x,y\in V\,$:
- $\langle x,\alpha y\rangle = \alpha\langle x,y\rangle$
- $\langle x,y+z\rangle = \langle x,y\rangle + \langle x,z\rangle$
It can be shown that every inner product space is a normed space, with norm:
$$ \|x\| = \sqrt{\langle x,x\rangle} $$Thus, every inner product space is also a metric space, with metric:
$$ d(x,y) = \|x-y\| $$If $\,V\,$ is an inner product space which is complete in the metric induced by the inner product, then $\,V\,$ is called a Hilbert space.
Let $\, x=(x_1,\ldots,x_n)\,$ and $\,y = (y_1,\ldots,y_n)\,$ be vectors in $\,\Bbb R^n\,.$ Then,
$$ \langle x,y\rangle := x_1y_1 + \cdots + x_ny_n $$defines an inner product on $\,\Bbb R^n\,,$ that induces the standard norm and metric on $\,\Bbb R^n\,.$ It is a consequence of the previous theorem that $\,\Bbb R^n\,$ with this inner product is a Hilbert space.
The Schwarz inequality, given next, describes the relationship between an inner product and its induced norm:
Let $\,V\,$ be an inner product space with inner product $\,\langle \ ,\,\rangle\,$ and induced norm $\,\|\ \|\,.$ Then, for all $\,x,y\in V\,$:
$$ |\langle x,y\rangle| \le \|x\|\,\|y\| $$By the Schwarz Inequality, if $\,x\,$ and $\,y\,$ are any nonzero vectors in an inner product space, then:
$$ -1\le \frac{\langle x,y\rangle}{\|x\|\,\|y\|} \le 1 $$Consequently, there is a unique angle $\,0\le \theta \le \pi\,$ satisfying $\,\cos\theta = \frac{\langle x,y\rangle}{\|x\|\,\|y\|}\,.$ If, in addition, $\,\langle x,y\rangle = 0\,,$ then $\,\cos\theta = 0\,$ and hence $\,\theta = \frac\pi 2\,.$ In this case, $\,x\,$ and $\,y\,$ are said to be orthogonal.
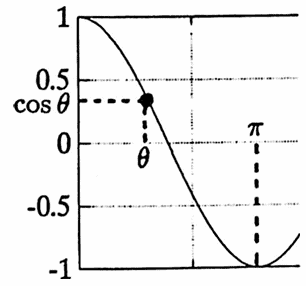
These observations help to justify the following definition:
Let $\,V\,$ be an inner product space with inner product $\,\langle\ ,\,\rangle\,$ and induced norm $\,\|\,\|\,.$ If $\,x\,$ and $\,y\,$ are nonzero vectors in $\,V\,,$ then the angle $\,\theta\,$ between $\,x\,$ and $\,y\,$ is the unique angle $\,0\le\theta\le\pi\,$ satisfying:
$$ \cos\theta = \frac{\langle x,y\rangle}{\|x\|\,\|y\|} $$For all $\,x,y\in V\,,$ $\,x\,$ and $\,y\,$ are orthogonal (or perpendicular) if and only if $\,\langle x,y\rangle = 0\,.$ A set of vectors is mutually orthogonal if every distinct pair chosen from the set is orthogonal.
If $\,x\,$ is orthogonal to every vector in a set $\,W\,,$ then $\,x\,$ is said to be orthogonal to $\,W\,.$
A set of vectors $\,\{x_1,\ldots,x_n\}\,$ is orthonormal if the vectors are mutually orthogonal, and if each vector in the set has norm $\,1\,.$
It is routine to verify that if $\,S\,$ is any set of mutually orthogonal vectors that does not contain the zero vector, then $\,S\,$ is linearly independent.
Let $\,V\,$ be an inner product space, and let $\,u\in V\,.$ Suppose $\,v\in V\,$ has length $\,1\,.$ The vector
$$ \langle u,v\rangle v $$is called the orthogonal projection of $\,u\,$ on $\,v\,.$ The name is justified, since $\,\langle u,v\rangle v\,$ is a scalar multiple of $\,v\,,$ and $\,u - \langle u,v\rangle v\,$ is orthogonal to $\,v\,$:
$$ \begin{align} \langle u - \langle u,v\rangle v\,,\,v\rangle &= \langle u,v\rangle - \langle u,v\rangle\langle v,v\rangle\cr\cr &= \langle u,v\rangle - \langle u,v\rangle (1)\cr\cr &= 0 \end{align} $$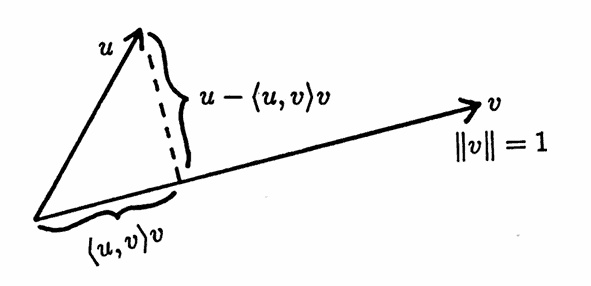
More generally, if $\,W\,$ is a subspace with orthonormal basis $\,v_1,\ldots,v_n\,,$ and if $\,u\,$ is any vector in $\,V\,,$ then
$$ w_1 := \langle u,v_1\rangle v_1 + \cdots + \langle u,v_n\rangle v_n $$is the orthogonal projection of $\,u\,$ on $\,W\,,$ and $\,w_2 := u - w_1\,$ is the component of $\,u\,$ orthogonal to $\,W\,.$ Clearly, $\,w_1\in W\,.$ It is routine to verify that $\,w_2\,$ is orthogonal to $\,W\,.$
The projections thus defined are used in the Gram-Schmidt orthogonalization procedure, discussed next. This procedure is used in Section 2.3, Discrete Orthogonal Functions.
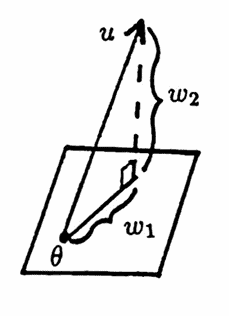
Let $\,S = \{u_1,\ldots,u_n\}\,$ be any set of linearly independent vectors in an inner product space. The Gram-Schmidt orthogonalization procedure converts $\,S\,$ to a set $\,\{v_1,\ldots,v_n\}\,$ of orthonormal vectors with the same span as S, as follows:
- Define $\,v_1 := \frac{u_1}{\|u_1\|}\,.$
- To get $\,v_2\,,$ project $\,u_2\,$ onto the subspace spanned by $\,v_1\,,$ and then normalize it: $$ v_2 := \frac{u_2 - \langle u_2,v_1\rangle v_1}{\|u_2 - \langle u_2,v_1\rangle v_1\|} $$
- To get $\,v_3\,,$ project $\,u_3\,$ onto the subspace spanned by $\,v_1\,$ and $\,v_2\,$: $$ v_3 := \frac{u_3 - \langle u_3,v_1\rangle v_1 - \langle u_3,v_2\rangle v_2} {\|u_3 - \langle u_3,v_1\rangle v_1 - \langle u_3,v_2\rangle v_2\|} $$
- Continue in this fashion, obtaining $\,v_{i+1}\,$ by projecting $\,u_{i+1}\,$ onto the subspace spanned by $\,\{v_1,\ldots,v_i\}\,.$
In the next theorem, the notation ‘inf ’ denotes the infimum of a set of real numbers, that is, the greatest lower bound.
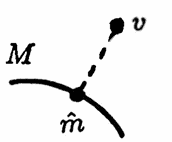
[Krey, p. $144$] Let $\,V\,$ be an inner product space and $\, M\ne\emptyset\,$ a convex subset which is complete (in the metric induced by the inner product). Then for every given $\,v\in V\,$ there exists a unique $\,\hat m\in M\,$ such that:
$$ \underset{m\in M}{\text{inf}} \|v-m\| = \|v - \hat m\| $$This theorem is applied next to the least-squares minimization problem:
Let $\,X\,$ be an $\,n \times m\,$ matrix with real entries, and let $\,y\in\Bbb R^n\,.$ Then, there exists a solution to the least-squares problem:
$$ \underset{b\in\Bbb R^m}{\text{inf}} \|y - Xb\| \tag{1} $$The following conditions are equivalent:
a) The solution is unique.
b) $\text{ker}(X) = \{0\}\,,$ where $\,0\,$ is the $\,m \times 1\,$ zero vector.
c) The columns of $\,X\,$ are linearly independent in $\,\Bbb R^n\,$.
Let $\,X\in\Bbb R^{n\times m}\,$ and let $\,y\in\Bbb R^n\,.$ The range of $\,X\,$ is a subspace of $\,V = \Bbb R^n\,$; call this subspace $\,M\,.$ Since
$$ \begin{align} &\{ \|y - m\|\ |\ m\in M \}\cr\cr &\qquad = \{ \|y-Xb\|\ |\ b\in\Bbb R^m\}\ , \end{align} $$it follows that if a solution to
$$ \underset{m\in M}{\text{inf}} \|y-m\| \tag{2} $$exists, then so does a solution to $(1)$. For if $\,\hat m\,$ solves $(2)$, then choose $\,\hat b\in\Bbb R^m\,$ with $\,\hat m = X\hat b\,.$ Then, $\,\hat b\,$ is a solution to $(1)$.
Since subspaces are convex, and since finite-dimensional subspaces are complete, the Minimizing Vector Theorem guarantees a solution to $(2)$, and hence a solution to $(1)$.
It is next proven that $\,\text{a)}\Rightarrow \text{b)}\Rightarrow \text{c)}\Rightarrow \text{a)}\,,$ completing the proof.
Suppose that the solution to $(1)$ is unique; call it $\,b\,.$ Suppose for contradiction that there exists $\,x\ne 0\,$ in $\,\text{ker}(X)\,.$ Then,
$$ X(b+x) = Xb + Xx = Xb\,, $$so that:
$$ \|y - Xb\| = \|y - X(b+x)\| $$Therefore, $\,b+x\,$ is a different solution to $(1)$, providing the desired contradiction.
Suppose $\,\text{ker}(X) = \{0\}\,.$ Since
$$ m = \text{dim} \bigl( \text{ker}(X) \bigr) + \text{dim}(\text{range of } X)\ , $$it follows that the range of $\,X\,$ has dimension $\,m\,.$ Therefore, the $\,m\,$ columns of $\,X\,$ must be linearly independent.
Suppose the columns of $\,X\,$ are linearly independent. Again, since
$$ m = \text{dim} \bigl( \text{ker}(X) \bigr) + \text{dim}(\text{range of } X)\ , $$it follows that $\,\text{ker}(X) = \{0\}\,.$ Suppose $\,b_1\,$ and $\,b_2\,$ are both solutions of $(1)$. Then:
$$ \|y - Xb_1\| = \|y - Xb_2\| $$But, since solutions to $(2)$ are unique, and since both $\,Xb_1\,$ and $\,Xb_2\,$ are in $\,M\,,$ it must be that $\,Xb_1 = Xb_2\,,$ from which $\,X(b_1 - b_2) = 0\,.$ Thus, $\,b_1 - b_2\in\text{ker}(X)\,,$ from which $\,b_1 = b_2\,.$ Thus, solutions are unique. $\blacksquare$
Let $\,f_1(t) = t\,$ and $\,f_2(t) = 2t\,.$ Let $\,T = (0,1,2)\,.$ Then, $\,f_1(T) = (0,1,2)\,$ and $\,f_2(T) = (0,2,4)\,.$ The matrix $\,X\,$ that arises in the linear least-squares approximation problem (see Section 2.2) is defined via $\,X_{ij} = f_j(t_i)\,.$ Thus:
$$ X = \begin{bmatrix} 0 & 0\cr 1 & 2\cr 2 & 4 \end{bmatrix} $$It is routine to verify that:
$$ \begin{align} \text{ker}(X) &= \{(t,-\frac t2)\ |\ t\in\Bbb R\}\cr &\ne \{0\} \end{align} $$Let $\,y = (0,1,2) \in\Bbb R^3\,.$ In this case, there are an infinite number of solutions to the least-squares problem $\,\text{min}_{b\in\Bbb R^2} \|y - Xb\|^2\,,$ as follows:
$$ \begin{align} \|y - Xb\| = 0 &\iff y - Xb = 0\cr\cr &\iff \begin{bmatrix} 0 \\ 1 \\ 2 \end{bmatrix} - \begin{bmatrix} 0 \\ b_1 + 2b_2 \\ 2b_1 + 4b_2\end{bmatrix} = \begin{bmatrix} 0\cr 0\cr 0\end{bmatrix}\cr\cr &\iff b_1 + 2b_2 = 1\cr\cr &\iff b_2 = \frac 12(1 - b_1) \end{align} $$In particular, all functions of the form $\,Kf_1\,$ and $\,\frac 12(1-K)f_2\,$ solve the least-squares problem.
It was noted in Section 2.2 that if $\,X^tX\,$ is invertible, then there is a unique solution to the linear least-squares approximation problem. However, in this example,
$$ X^tX = \begin{bmatrix} 5 & 10\cr 10 & 20 \end{bmatrix} $$is not invertible, since it has determinant $\,0\,.$ Note also that the columns of $\,X\,$ are not linearly independent, since the second column is a multiple of the first.
Much of the material discussed in Section 2.3 is conveniently expressed in terms of the singular values of $\,A\,.$ Important definitions and results are briefly summarized here. The remainder of this appendix can be skipped without any loss of continuity.
By definition, a real $\,m \times m\,$ matrix $\,Q\,$ is orthogonal if $\,Q^t Q = I\,,$ where $\,I\,$ is the $\,m \times m\,$ identity matrix. Equivalently, $\,Q\,$ is orthogonal if and only if $\,Q^t = Q^{-1}\,.$ If $\,Q\,$ is orthogonal, then it can be shown that the columns (rows) of $\,Q\,$ form an orthonormal basis for $\,\Bbb R^m\,$ [G&VL, p. $70$].
If $\,A\,$ is any real $\,m \times n\,$ matrix, then it can be shown that there exist orthogonal matrices $\,U\in\Bbb R^{m\times m}\,$ and $\,V\in\Bbb R^{n\times n}\,$ such that
$$ \begin{gather} U^t AV = \text{diag}(\sigma_1,\ldots,\sigma_p) \in \Bbb R^{m\times n}\,,\cr p = \text{min}\{m,n\}\,, \end{gather} $$where $\sigma_1 \ge \sigma_2 \ge \cdots \ge \sigma_p \ge 0\,,$ and where $\,\text{diag}(\sigma_1,\ldots,\sigma_p)\,$ denotes the matrix with $\,\sigma_i\,$ in row $\,i\,$ and column $\,i\,,$ and with zeroes elsewhere [G&VL, p. $71$].
By definition, the $\,\sigma_i\,$ are the singular values of $\,A\,.$ The largest singular value, $\,\sigma_1\,,$ is also denoted by $\,\sigma_{\text{max}}\,.$
Both the $2$-norm and Frobenius norm of a matrix $\,A\,$ are neatly characterized in terms of the singular values of $\,A\,$ [G&VL, p. $72$]:
$$ \begin{align} \|A\|_F &= \sqrt{\sigma_1^2 + \cdots + \sigma_p^2}\,,\ \ p = \text{min}\{m,n\}\,,\cr\cr \|A\|_2 &= \sigma_{\text{max}} \end{align} $$There is a beautiful relationship between the singular values of $\,A\,$ and the eigenvalues of $\,A^t A\,,$ as follows:
$$ \begin{align} &U^t AV = \text{diag}(\sigma_1,\ldots,\sigma_p)\cr\cr &\qquad \implies (U^t AV)^t = \text{diag}(\sigma_1,\ldots,\sigma_p)\cr\cr &\qquad \implies V^t A^t U = \text{diag}(\sigma_1,\ldots,\sigma_p)\cr\cr &\qquad \implies (V^t A^t U)(U^t AV) = \text{diag}(\sigma_1^2,\ldots,\sigma_p^2)\cr\cr &\qquad \implies V^t(A^t A)V = \text{diag}(\sigma_1^2,\ldots,\sigma_p^2)\cr\cr &\qquad \implies A^t A = V\,\text{diag}(\sigma_1^2,\ldots,\sigma_p^2)\,V^t \end{align} $$Thus, $\,A^t A\,$ is similar to $\,\text{diag}(\sigma_1^2,\ldots,\sigma_p^2)\,.$ Since similar matrices have the same eigenvalues, and since the eigenvalues of a diagonal matrix lie on the diagonal, it follows that $\,A^t A\,$ has eigenvalues $\,\sigma_1^2,\ldots,\sigma_p^2\,.$ Thus, the singular values of $\,A\,$ (which are, by definition, nonnegative numbers) are the square roots of the eigenvalues of $\,A^t A\,.$