The Right Triangle Approach to Trigonometry

There are two basic approaches to trigonometry:

• the right triangle approach (this section)
• the unit circle approach (next section)

Both approaches were introduced in Introduction to Trigonometry. Be sure to read this prior section, since it covers important notation and conventions.

The Right Triangle Approach to Trigonometry

Start with a right triangle (i.e., a triangle with a $\,90^{\circ}$ angle). (Don't despair! From these humble beginnings, tools for any triangle will be developed!)

Focus attention on one of the two acute angles. Whichever one you choose, call it $\,\theta\,.$

Relative to $\,\theta\,,$ names are given to the lengths of the sides (see diagram below):

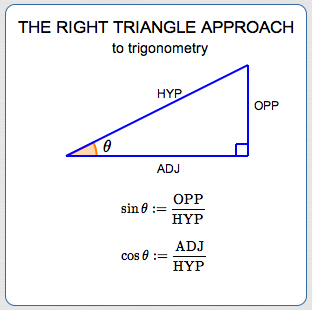
• The side opposite (across from) $\,\theta\,$ is called OPP (for OPPosite)
• The non-hypotenuse side adjacent to (next to) $\,\theta\,$ is called ADJ (for ADJacent)

The hypotenuse is the longest side in the triangle. It is the side opposite the right angle. The hypotenuse is called HYP (for HYPotenuse).

Define:

(Recall that ‘$\,:=\,$’ means ‘equals, by definition’.) Since the hypotenuse is the longest side, both of these ratios are less than $\,1\,.$

There are four more trigonometric functions, each of which are defined in terms of sine and cosine. One of these is the tangent function:

There is a common memory device to remember the ‘right triangle’ definitions of sine, cosine, and tangent:

SOHCAHTOA
(pronounced ‘SEW - CA - TOE - UH’)

Sine  Opposite  Hypotenuse
Cosine  Adjacent  Hypotenuse
Tangent  Opposite  Adjacent

The trigonometric functions aren't quite as simple as (say) $\,f(x) = x^2 + 1\,.$ This (sample) function $\,f\,$ uses its input in a very direct way: it squares it, and then adds $\,1\,.$

However, the way the sine function uses its input, $\,\theta\,,$ isn't quite as direct! First, an acute angle $\,\theta\,$ can be used to get a right triangle with a known shape (and the size doesn't matter). Then, $\,\sin\theta\,$ is found by taking a particular ratio of the lengths of two sides. The input still uniquely determines the output—there's just an intermediate step!

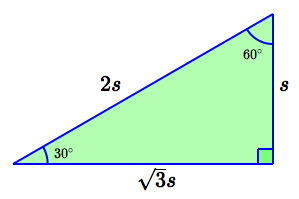
There are infinitely many right triangles with a given angle between zero and $\,90^\circ\,.$ For example, there are infinitely many $\,30^\circ$-$60^\circ$-$90^\circ\,$ triangles; they can all be summarized by using a scaling factor, $\,s\,,$ as shown below. However, the actual size of the triangle doesn't matter when computing the trigonometric ratios, since the scaling factor $\,s\,$ cancels out.

Note that the right triangle approach naturally lends itself only to finding the sine and cosine of angles between $\,0^\circ\,$ and $\,90^\circ\,.$ You can't have (say) a $\,100^\circ\,$ angle in a right triangle!

Sometimes, angles between $\,0^\circ\,$ and $\,90^\circ\,$ are all you need, and then the right triangle approach may be simplest. For more generality, you'll use the unit circle approach, or a combination of the two approaches!

Trigonometric Ratios

The fractions $\,\frac{\text{OPP}}{\text{HYP}}\,,$ $\,\frac{\text{ADJ}}{\text{HYP}}\,$ and $\,\frac{\text{OPP}}{\text{ADJ}}\,$ are often referred to as the ‘trigonometric ratios’.

Here's an example, using the familiar $\,30^\circ$-$60^\circ$-$90^\circ\,$ triangle:

Example: Finding the Trigonometric Ratios in a Right Triangle with Known Legs

Consider a right triangle with legs of lengths $\,5\,$ and $\,7\,.$ Let $\,\theta\,$ be the largest acute angle. Find $\,\sin\theta\,,$ $\,\cos\theta\,,$ and $\,\tan\theta\,.$ (It is not necessary to simplify radicals or to rationalize denominators.)

Solution:  By the Pythagorean Theorem,

Therefore,

The largest acute angle is opposite the longest leg.

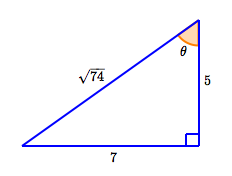
Thus:

Note: Suppose that the right triangle had legs of lengths $\,500\,$ and $\,700\,$ (instead of $\,5\,$ and $\,7\,$). Then, you would first ‘shrink’ the triangle to a more manageable size, by dividing the lengths by $\,100\,.$ Similar triangles have the same angles! Don't work with big numbers when you don't have to!

Or, suppose the right triangle had legs of lengths $\,0.00005\,$ and $\,0.00007\,$ (instead of $\,5\,$ and $\,7\,$). You would first ‘stretch’ the triangle by multiplying the lengths by $\,100{,}000\,.$ Similar triangles have the same angles! Don't work with very small numbers when you don't have to!