 Fundamental Trigonometric Identities
Fundamental Trigonometric Identities
Trigonometry is abundant with identities—they provide important renaming tools when working with trigonometric expressions.
Three of the most basic trigonometric identities are discussed in this section, after a quick review of the word ‘identity’.
| The Pythagorean Identity: | $\,\sin^2 t + \cos^2 t = 1\,$ |
| Cosine is an Even Function: | $\,\cos (-t) = \cos t\,$ |
| Sine is an Odd Function: | $\,\sin (-t) = -\sin t\,$ |
What is an ‘Identity’?
An identity is a mathematical sentence that is always true.
Strictly speaking, ‘1 + 1 = 2’ is an identity. However, the word ‘identity’ is typically reserved for a sentence with one or more variables, that is true for every possible choice of variable(s).
For example, $\,(x+y)^2 = x^2 + 2xy + y^2\,$ is an identity from algebra. No matter what real numbers are chosen for $\,x\,$ and $\,y\,,$ the equation is true. For example, letting $\,x = 2\,$ and $\,y = -3\,$ gives:
- Left side: $$\cssId{s17}{(x+y)^2 = (2-3)^2 = (-1)^2 \color{red}{= 1}}$$
-
Right side:
$$ \begin{align} &x^2 + 2xy + y^2 \cr &\quad = 2^2 + 2(2)(-3) + (-3)^2\cr &\quad = 4 - 12 + 9 \color{red}{= 1} \end{align} $$
The left and right sides will always be equal, regardless of the choices made for $\,x\,$ and $\,y\,.$
In this case, it is a simple application of FOIL to see why the equation is always true:
$$\cssId{s22}{(x+y)^2 = (x+y)(x+y) = x^2 + 2xy + y^2}$$However, identities are not always this obvious—it is not always this easy to prove that a given sentence is an identity!
What Good are Identities?
Identities can provide tremendous renaming power.
For example, the identity above allows the expressions $\,(x+y)^2\,$ and $\,x^2 + 2xy + y^2\,$ to be substituted, one for the other, whenever it is convenient to do so.
In particular, renaming $\,x^2 + 2xy + y^2\,$ as $\,(x+y)^2\,$ (a perfect square) shows that it is always nonnegative. The sum $\,x^2 + 2xy + y^2\,$ doesn't readily reveal that it can't ever be negative—but the perfect square $\,(x+y)^2\,$ does. Different names can reveal different properties of numbers!
The Pythagorean Identity: $\,\sin^2 t + \cos^2 t = 1$
The Pythagorean Identity, $\,\sin^2 t + \cos^2 t = 1\,,$ is perhaps the most used and most famous trigonometric identity. Remember—when a mathematical result is given a special name, there's a reason!
The Pythagorean Identity follows immediately from the unit circle definition of sine and cosine :
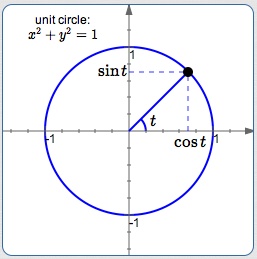
- Recall that, in trigonometry, ‘unit circle’ refers to the circle of radius $\,1\,$ that is centered at the origin. The equation of the unit circle is: $x^2 + y^2 = 1$
- By definition, cosine and sine give the $\,x\,$ and $\,y\,$ values (respectively) of points on the unit circle. That is, for every real number $\,t\,$ (which can be thought of as the radian measure of an angle, if desired), $\,\bigl(\cos t,\sin t\bigr)\,$ is a point on the unit circle.
- Since $\,(\cos t,\sin t)\,$ is on the circle $\,x^2 + y^2 = 1\,,$ it satisfies the equation. That is, substitution of ‘$\,\cos t\,$’ for ‘$\,x\,$’ and ‘$\,\sin t\,$’ for ‘$\,y\,$’ makes the equation true: $$ \cssId{s43}{(\cos t)^2 + (\sin t)^2 = 1} $$
-
The expression ‘$\,\sin^2 t\,$’ is a common abbreviation for ‘$\,(\sin t)^2\,$’. (You save writing two parentheses!)
Similarly, ‘$\,\cos^2 t\,$’ is a common abbreviation for ‘$\,(\cos t)^2\,$’.
(More generally, this abbreviation is also used for powers $\,3, 4, 5, \ldots\,.$ )
- Using these abbreviations and switching the order of the sum gives the Pythagorean Identity: $$ \cssId{s49}{\sin^2 t + \cos^2 t = 1} $$
Why the Name ‘the Pythagorean Identity’?
Look at the green triangle shown below, in the first quadrant, in the unit circle:
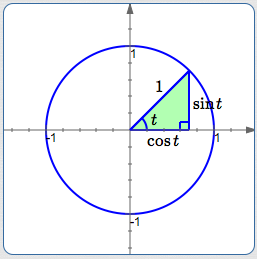
- The bottom leg has length $\,\cos t$
- The other leg has length $\,\sin t$
- The hypotenuse has length $\,1$
A quick application of the Pythagorean Theorem gives:
$$ \cssId{s56}{\sin^2 t + \cos^2 t = 1^2 = 1} $$Voila! The Pythagorean Identity!
Cosine is an Even Function
Recall that even functions have the property that when inputs are opposites, outputs are the same:
- The numbers $\,-t\,$ and $\,t\,$ are opposites, for all real numbers $\,t\,.$
- Their corresponding outputs from a function $\,f\,$ are $\,f(-t)\,$ and $\,f(t)\,.$
- For even functions, these two outputs must (always) be equal: $\,f(-t) = f(t)\,.$
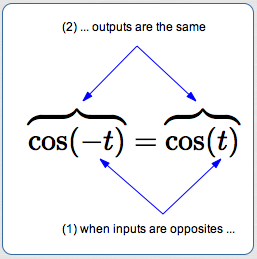
Cosine has this property:
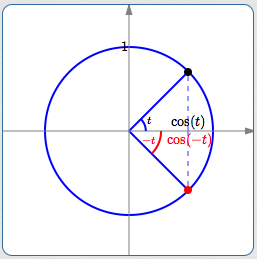
By definition:
- The terminal point for $\,t\,$ has $x$-value equal to $\,\cos(t)$
- The terminal point for $\,\color{red}{-t}\,$ has $\color{red}{x}$ -value equal to $\,\color{red}{\cos(-t)}$
From symmetry, these two $x$-values are always the same!
Sine is an Odd Function
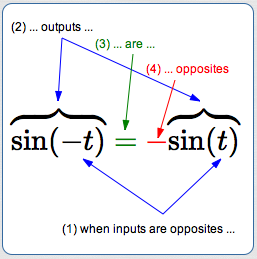
Recall that odd functions have the property that when inputs are opposites, outputs are also opposites:
- The numbers $\,-t\,$ and $\,t\,$ are opposites, for all real numbers $\,t\,.$
- Their corresponding outputs from a function $\,f\,$ are $\,f(-t)\,$ and $\,f(t)\,.$
- For odd functions, these two outputs must (always) be opposites: $\,f(-t) = -f(t)\,.$
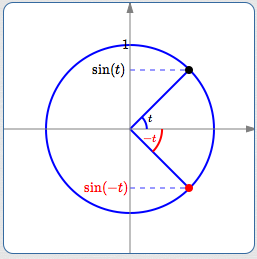
Sine has this property:
By definition:
- The terminal point for $\,t\,$ has $y$-value equal to $\,\sin(t)$
- The terminal point for $\,\color{red}{-t}\,$ has $\color{red}{y}$ -value equal to $\,\color{red}{\sin(-t)}$
From symmetry, these two $y$-values are always opposites:
$$ \cssId{s81}{\overbrace{\strut\sin(-t)}^{\text{sine of $-t$}}\ \ \ \overbrace{\strut =}^{\text{is}}\ \ \ \overbrace{\strut -}^{\text{the opposite of}}\ \ \ \overbrace{\strut\sin(t)}^{\text{sine of $t$}}} $$