Introduction to Equations and Inequalities in Two Variables

Want some practice with preliminary concepts first?

An equation is a sentence that uses an equals sign: $\,=\,$

An inequality is a sentence that uses an inequality symbol:

$\cssId{s6}{\gt}$	greater than
$\cssId{s7}{\lt}$	less than
$\cssId{s8}{\ge}$	greater than or equal to
$\cssId{s9}{\le}$	less than or equal to

The phrase in two variables means that two different variables are used to determine if the sentence is true. In other words, you'll be choosing values for two different variables, and substituting these into the sentence, to decide if it is true or false.

Most sentences in two variables are easy to spot, because you can ‘see’ two different variables. Here's a simple example, to introduce important concepts and terminology:

Example (An Equation in Two Variables)

‘$\,x + y = 5\,$’ is an equation in two variables.
It's an ‘equation’ because of the ‘$\,=\,$’ sign.
It's ‘in two variables’ because two different variables, $\,x\,$ and $\,y\,,$ are used to determine if the equation is true.
Terminology used: we say this is an ‘equation in $\,x\,$ and $\,y\,$’.
When $\,x = 1\,$ and $\,y = 4\,,$ the equation is true: $\,1 + 4 = 5\,$
When $\,x = -1.5\,$ and $\,y = 6.5\,,$ the equation is true: $\,-1.5 + 6.5 = 5\,$
Most interesting sentences in two variables (like this one) have an infinite number of choices for the two variables that make the sentence true.
A solution of a sentence in two variables is a choice for each of the variables that makes the sentence true.
Usually, the solutions are reported as ordered pairs—you have to agree on the order that you list the variables. When the two variables are $\,x\,$ and $\,y\,$ (which they often are), there's a very strong convention that you list $\,x\,$ first and $\,y\,$ second. Always use this convention!
Thus, the ordered pair $\,(1,4)\,$ (a shorthand for $\,x=1\,$ and $\,y=4\,$) is a solution of the equation $\,x + y = 5\,.$
Also, the point $\,(-1.5,6.5)\,$ is a solution of the equation $\,x + y = 5\,.$

Terminology: We can say ‘$\,(-1.5,6.5)\,$ satisfies the equation $\,x + y = 5\,$’. Perhaps think of it this way: if equations had feelings, then this equation would be happy (would be satisfied), because it would be true!
Observe that ‘a solution’ is an ordered pair. Thus, a solution consists of two numbers: a choice for each of the variables.
Each solution (each ordered pair) corresponds to a point in the coordinate plane. The picture of all the solutions, in a coordinate plane, is called the graph of the sentence in two variables. A graph is an extremely powerful way to understand an equation/inequality in two variables.
Throughout your math experience, you'll study different types of equations/inequalities, and see that they have different types of graphs.

Now comes the really fun part. Jump over to wolframalpha.com and type in the equation $\,x + y = 5\,.$ You'll get various information, and a graph:

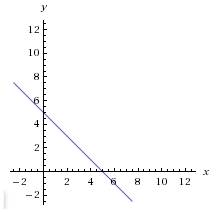
Ah hah! So, the picture of all the points that makes the equation $\,x+y = 5\,$ true is a line!

See where the line crosses the $\,y$-axis? That's the point $\,(0,5)\,$: $\,0 + 5 = 5\,$

See where the line crosses the $\,x$-axis? That's the point $\,(5,0)\,$: $\,5 + 0 = 5\,$

Find the (approximate) location of the solutions $\,(1,4)\,$ and $\,(-1.5,6.5)\,$ on the line.

You'll want to bookmark wolframalpha.com. When you're bored, just type in equations and inequalities (you can start with the ones mentioned on this page) and see what you get.

Example (An Inequality in Two Variables)

The sentence $\,x + y\ge 5\,$ is an inequality in two variables. It's an inequality because of the ‘$\,\ge\,$’ sign.

If you graph it at wolframalpha.com, you'll need to type it in like this:

x + y >= 5

(You can just cut-and-paste, if you want.) Here's what you'll see:

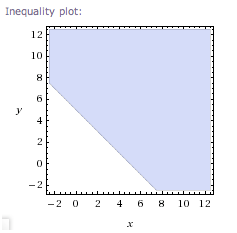
Of course, you can only see part of the graph—it goes on forever in all directions. In this case, you're looking at all the points that are on or above the graph of $\,x + y = 5\,.$ Also, be careful—they're not showing the $\,x$-axis and the $\,y$-axis in this view: the bottom line isn't isn't the $x\,$-axis, and the left vertical line isn't the $y\,$-axis.

Example (A More Complicated Equation in Two Variables)

The sentence $\,x^2 - 3xy + y^2 + 3x - 5y + 7 = 0\,$ is an equation in two variables. The variables can appear any number of times; there just can't be more than two different variables.

If you graph it at wolframalpha.com, type it in like this:

x^2 - 3xy + y^2 + 3x - 5y + 7 = 0

(You can just cut-and-paste, if you want.)

Example (A Tricky Type of Equation in Two Variables— An ‘Invisible’ Variable)

One tricky type of ‘sentence in two variables’ is where you don't actually see two different variables, since one of them has a coefficient of $\,0\,.$ What does this mean, exactly?

Consider the equation $\,x = 5\,.$ It looks like there's only one variable, $\,x\,.$ Viewed as an equation in one variable, there's only one solution—the number $\,5\,.$ In this case, the graph is very, very boring—a single dot, at location $\,5\,,$ on a number line.

However, the sentence $\,x = 5\,$ can also be viewed as an equation in two variables: $\,x + 0y = 5\,.$ We don't bother to write the $\,0y\,,$ since it's just zero—but it changes the solution set completely. Now, since it's an equation in two variables, a solution is an ordered pair—a choice for $\,x\,$ and a choice for $\,y\,$—that make the equation true.

What you notice pretty quickly is that $\,x\,$ must be $\,5\,,$ but $\,y\,$ can be anything:

$(5,1)\,$ is a solution, since substituting $\,5\,$ for $\,x\,$ and $\,1\,$ for $\,y\,$ in ‘$\,x + 0y = 5\,$’ gives this true statement: $$\cssId{s108}{5 + 0(1) = 5}$$
Similarly, $(5,\frac12)\,$ is a solution, since $\,5 + 0(\frac12) = 5\,.$
Indeed, $(5,\text{anything})\,$ is a solution, since $\,5 + 0(\text{anything}) = 5\,.$

Thus, the solutions are ordered pairs of the form $\,(5,y)\,,$ for all real numbers $\,y\,.$ What does this graph look like? To get to any of these points, you start at the origin and move $\,5\,$ units to the right. Then, you can move up/down to your heart's content. The graph is the vertical line that crosses the $\,x$-axis at $\,5\,$:

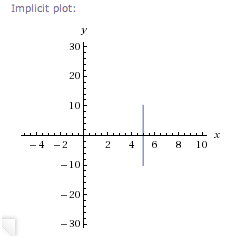
graph of x = 5, viewed as an equation in two variables

Wolfram Alpha has a bit of trouble with this one. Give it a break—it's a bit hard to see invisible things.

But, we can get a great approximation to the graph by being a bit clever. Cut-and-paste the following into wolframalpha.com:

x + 0.00000001y = 5, -10 <= y <= 10

Notice that we've put a number really close to $\,0\,$ in front of the $\,y\,.$ We're also specifying that we only want to see points whose $\,y$-values are between $\,-10\,$ and $\,10\,.$ (Leave off the last part and see if you can figure out what's happening!)

By the way, wolframalpha.com can plot it easily with just one word's help:

plot x = 5

Try it!

So, what's a person to do when they see an equation like ‘$\,x = 5\,$’? Treat it as an equation in one variable? In two variables? (In three variables!?) Context, context, context. If someone says ‘graph $\,x=5\,$’ in high school, then they're probably treating it as an equation in two variables. If there's any doubt, just ask for clarification.

Solutions of equations/inequalities in two variables

Let $\,S\,$ denote an equation or inequality in two variables ($\,x\,$ and $\,y\,$). Then, the following are equivalent:

$(a,b)\,$ lies on the graph of $\,S\,$
$(a,b)\,$ satisfies $\,S\,$
substitution of $\,a\,$ for $\,x\,,$ and $\,b\,$ for $\,y\,,$ makes the sentence $\,S\,$ true

Examples

Question: Does the point $\,(1,-2)\,$ lie on the graph of $\,2x + 3y = -4\,$?

Solution: Yes, since the equation ‘$\,2(1) + 3(-2) = -4\,$’ is true.

Question: Does the point $\,(0,-1)\,$ satisfy the equation $\,2x + 3y = -4\,$?

Solution: No, since the equation ‘$\,2(0) + 3(-1) = -4\,$’ is false.

Question: Does the point $\,(3,-1)\,$ lie on the graph of $\,x = 3\,$?

Solution: Yes, since substitution of $\,3\,$ for $\,x\,$ makes the equation true. Observe that the equation $\,x = 3\,$ is being treated as an equation in two variables: $$\cssId{s155}{\,x + 0y = 3}$$ Here, we can ignore the $\,y$-value; all we care about is if $\,x\,$ is equal to $\,3\,.$

Question: Does the point $\,(3,5)\,$ satisfy the inequality $\,y\gt 4\,$?

Solution: Yes, since substitution of $\,5\,$ for $\,y\,$ makes the inequality true. Observe that the inequality $\,y \gt 4\,$ is being treated as an inequality in two variables: $$\cssId{s162}{0x + y \gt 4}$$ Here, we can ignore the $\,x$-value; all we care about is if $\,y\,$ is greater than $\,4\,.$

Question: Does the point $\,(3,5)\,$ satisfy the inequality $\,x \gt 4\,$?

Solution: No, since substitution of $\,3\,$ for $\,x\,$ makes the inequality false. Observe that the inequality $\,x \gt 4\,$ is being treated as an inequality in two variables: $$\cssId{s170}{x + 0y \gt 4}$$ Here, we can ignore the $\,y$-value; all we care about is if $\,x\,$ is greater than $\,4\,.$

Concept Practice

Sentences like ‘$\,x = 5\,$’ should be treated as sentences in two variables.