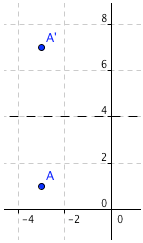
Practice With Points
Practice With Points
Want more basic practice with the coordinate plane and points first? Locating Points in Quadrants and on Axes
As discussed in Locating Points in Quadrants and on Axes, an ordered pair $\,(x,y)\,$ is a pair of numbers, separated by a comma, and enclosed in parentheses. The number that is listed first is called the first coordinate or the $x$-value. The number that is listed second is called the second coordinate or the $y$-value.
The coordinate plane (also called the $xy$-plane) is a device to ‘picture’ ordered pairs. Each ordered pair corresponds to a point in the coordinate plane, and each point in the coordinate plane corresponds to an ordered pair. For this reason, ordered pairs are often called points. Recall that the origin is the point $\,(0,0)\,.$
This section gives you practice with the connection between ordered pairs and movement in the coordinate plane.
Moving Up/Down/Left/Right
Left/right movement is controlled by the $x$-value (the first coordinate). Moving to the right increases the $x$-value; moving to the left decreases it. For example, if a point $\,(a,b)\,$ is moved two units to the right, then the new coordinates are $\,(a+2,b)\,.$ If a point $\,(a,b)\,$ is moved three units to the left, then the new coordinates are $\,(a-3,b)\,.$
Up/down movement is controlled by the $y$-value (the second coordinate). Moving up increases the $y$-value; moving down decreases it. For example, if a point $\,(a,b)\,$ is moved four units up, then the new coordinates are $\,(a,b+4)\,.$ If a point $\,(a,b)\,$ is moved five units down, then the new coordinates are $\,(a,b-5)\,.$
Recall that the origin is the point $\,(0,0)\,.$
Reflecting a Point about a Line
Suppose you have a line drawn on a piece of paper. On this same piece of paper, you have a point. For the moment, suppose that the point does not lie on the line.
To ‘reflect the point about the line’ means, roughly, that you want the point that is the same distance from the line, but on the other side of the line. This idea is illustrated below:
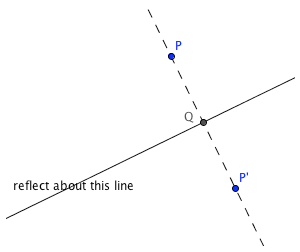
Reflecting about an arbitrary line: the distance from P to Q is the same as the distance from P' to Q. (The coordinates of the reflected point are not so easy to find.)
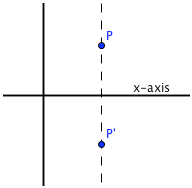
Reflecting about the $x$-axis: the $x$-value stays the same; take the opposite of the $y$-value.
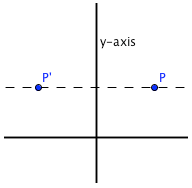
Reflecting about the $y$-axis: the $y$-value stays the same; take the opposite of the $x$-value.
Notice that if you fold the piece of paper along the line of reflection, then the original point and its reflection will land right on top of each other. It's kind of like reflecting in a mirror—except instead of the mirror reflecting ‘back at you’, it instead projects to the other side.
If a point actually lies on the line that you're reflecting about, then the reflection of the point is itself.
Examples
Why? $$ \begin{align} \cssId{s58}{(0,0)} \ \ &\cssId{s59}{\overset{\text{right 2}}{\rightarrow}}\ \ \cssId{s60}{(0+2,0) = (2,0)}\cr\cr &\cssId{s61}{\overset{\text{down 4}}{\rightarrow}}\ \ \cssId{s62}{(2,0-4) = (2,-4)} \end{align} $$
Why? $$ \begin{align} \cssId{s70}{(1,-3)} \ \ &\cssId{s71}{\overset{\text{left 4}}{\rightarrow}}\ \ \cssId{s72}{(1-4,-3) = (-3,-3)}\cr\cr &\cssId{s73}{\,\overset{\text{up 2}}{\rightarrow}}\ \ \cssId{s74}{(-3,-3+2) = (-3,-1)} \end{align} $$
Why? The up/down info (the $y$-value) gives distance from the $x$-axis. The left/right info (the $x$-value) gives distance from the $y$-axis. Thus:
| $(-2,5)$ | original point: currently $\,5\,$ units from the $x$-axis (above) and $\,2\,$ units from the $y$-axis (to the left) |
| $(-2,5\cdot 2) = (-2,10)$ | double distance from $x$-axis; stay above |
| $(-2\cdot 3,10) = (-6,10)$ | triple distance from $y$-axis, stay to the left |
To reflect about the $x$-axis, the $x$-value stays the same, and you take the opposite of the $y$-value.
To reflect about the $y$-axis, the $y$-value stays the same, and you take the opposite of the $x$-value.
Why? $$ \begin{align} \cssId{s120}{(-3,7)} \ \ &\cssId{s121}{\overset{\text{reflect about x-axis}}{\rightarrow}}\ \ \cssId{s122}{(-3,-7)}\cr\cr &\cssId{s123}{\overset{\text{reflect about y-axis}}{\rightarrow}}\ \ \cssId{s124}{(3,-7)} \end{align} $$
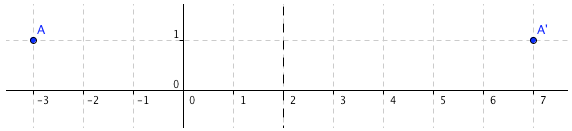
Why? On this problem, you need to stop and think. It might be helpful to make a sketch (see below).
- Since you're reflecting about a vertical line, the $y$-value won't change. It was $\,1\,,$ and it will remain $\,1\,.$
- Figure out the distance from the point to the line: $$\cssId{s137}{2 - (-3) = 5}$$ You need to go this far on the other side of the vertical line: $$\cssId{s139}{2 + 5 = 7}$$ So, the new $x$-value is $\,7\,.$
Why? Again, you need to stop and think. Again, a sketch may be helpful (see below).
- Since you're reflecting about a horizontal line, the $x$-value won't change. It was $\,-3\,,$ and it will remain $\,-3\,.$
- Figure out the distance from the point to the line: $$\cssId{s153}{4 - 1 = 3}$$ You need to go this far on the other side of the horizontal line: $$\cssId{s155}{4 + 3 = 7}$$ So, the new $y$-value is $\,7\,.$