The Angle Subtended by a Geometric Object at an External Point

This section is optional in the Precalculus course. It can be skipped without any loss of continuity. However, it offers an opportunity to introduce important ideas that don't typically make their way into Precalculus: path-connectedness, upper bounds and the least upper bound, and equivalent definitions.

• Motivation: Visual Acuity
• Definition: Geometric Object in a Plane
• Definition: Path-Connected
• Definition: Least Upper Bound (Supremum)
• The Notation, $\,\theta_{\mathcal G,P}\,,$ for the angle subtended by a geometric object $\,\mathcal G\,$ at an external point $\,P\,$
• Definition of $\,\theta_{\mathcal G,P}\,$
• Examples
• Equivalent Definitions
• Equivalent Definition of $\,\theta_{\mathcal G,P}\,$

Often, we want to ‘just capture’ an object inside an angle, relative to some external ‘viewing point’. The word ‘subtend’ is used in this context, as the examples below illustrate:

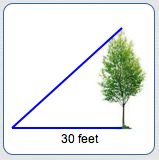
The angle subtended by a tree at a point 30 feet from the base of the tree

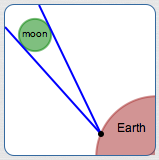
The angle subtended by the moon at a point on Earth (not to scale)

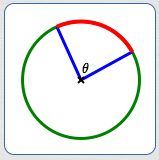
The angle ($\,\theta\,$) subtended by an arc (at the center of the circle)

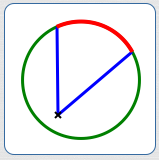
The angle subtended by an arc at a non-center point

The use of the word ‘subtend’ is a bit murky in the literature. Rarely do people seem to define it; when an attempt is made, it is usually for a specific occurrence of the idea. My genius husband (Ray) and I had fun defining the concept for a very general situation. Enjoy!

Motivation: Visual Acuity

First, a motivational discussion from a discipline that uses the word ‘subtend’ a lot!

Note: When a degree is divided into $\,60\,$ equal parts, each part is called a ‘minute’. The symbol  $'$  is used for minutes:

If you take a test for visual acuity, you'll likely find yourself reading letters off a chart on a wall (see an eye chart below).

An eye chart

When focusing on a particular letter, two lines are important: the line from the top of the letter to your eye, and the line from the bottom of the letter to your eye (see image below).

These two lines create an angle at your eye. For your information: typical charts are ‘calibrated’ so that a 20/20 letter makes an angle of $\,5'\,$ (five minutes, which equals $\,\frac{5}{60}^{\circ}\,$) at the eye.

All letters in the ‘viewing cone’ shown below would be seen with equal clarity—what matters is the angle that is made at the eye by those two lines that ‘just capture’ the object. Here's the language that is used in this situation: ‘each of these letters subtends the same visual angle at the eye’.

All letters in this ‘viewing cone’ would be seen with equal clarity; all these letters subtend the same angle at the eye.

Formulating the Definition: the Angle Subtended by a Geometric Object at an External Point

Some Preliminary Definitions

Definition: Geometric Object in a Plane

A geometric object in a plane is any set of points in a plane. A geometric object is nonempty if it contains at least one point.

Definition: Path-Connected

A geometric object is path-connected if, given any two points in the object, you can trace from one point to the other without leaving the geometric object. Roughly:

• A path-connected geometric object consists of exactly one ‘piece’
• A geometric object that is not path-connected has more than one ‘piece’

Some Geometric Objects in a Plane

Point

Several points

Spiral

Letter E

Filled polygon

Smiley face

Are they path-connected?

Path-connected

Not path-connected: tracing from one point to another takes you out of the set

Path-connected

Path-connected

Path-connected

Not path-connected: for example, you can't trace from one eye to the other without leaving the set

Motivation: the Least Upper Bound of a Set of Real Numbers

Take a look at the interval $\,[3,4)\,$ below: notice that the right endpoint isn't included.

What's the greatest number in this interval? The answer is—there isn't a greatest number that's in this interval!

The number $\,3.9\,$ is in the interval—but so is $\,3.91\,,$ and it's greater. The number $\,3.99\,$ is in the interval—but so is $\,3.991\,,$ and it's greater.

I think you see the problem. For situations like this, the concept of ‘least upper bound’ comes to the rescue.

Definition: the Least Upper Bound of a Set of Real Numbers (and Related Concepts)

Let $\,S\,$ be a nonempty set of real numbers.

By definition, an upper bound for $\,S\,$ is a real number $\,u\,$ such that $\,s \le u\,$ for all $\,s\in S\,.$ So, an upper bound for $\,S\,$ is just a number that's greater than or equal to everything in $\,S\,.$

There are infinitely many upper bounds for the interval $\,[3,4)\,.$ Here are a few:

• $\,5\,$ is an upper bound of $\,[3,4)\,$
• $\,4.5\,$ is an upper bound of $\,[3,4)\,$
• $\,4.1\,$ is an upper bound of $\,[3,4)\,$
• $\,4\,$ is an upper bound of $\,[3,4)\,$

Some upper bounds for the set $\,[3,4)$

By definition, a number $\,\ell\,$ is called the least upper bound of $\,S\,$ if:

• $\,\ell\,$ is an upper bound for $\,S\,$; and
• if $\,k\,$ is any upper bound for $\,S\,,$ then $\,\ell\le k$

The least upper bound of $\,S\,$ can be abbreviated as $\,\text{lub}(S)\,.$ The least upper bound is also called the supremum; the supremum of $\,S\,$ is denoted by $\,\sup(S)\,.$

Thus, of all possible upper bounds for $\,S\,,$ $\,\sup(S)\,$ is the least. (So, the name ‘least upper bound’ is appropriate!)

The least upper bound of the interval $\,[3,4)\,$ is $\,4\,.$ Why? Well, $\,4\,$ is an upper bound of $\,[3,4)\,.$ And, of all possible upper bounds for $\,[3,4)\,,$ $\,4\,$ is the least.

So, the interval $\,[3,4)\,$ doesn't have a greatest member, but it does have a least upper bound (a supremum).

Notation: $\,\theta_{\mathcal G,P}$

Let $\,\color{blue}{\mathcal G}\,$ be a nonempty path-connected geometric object in a plane.

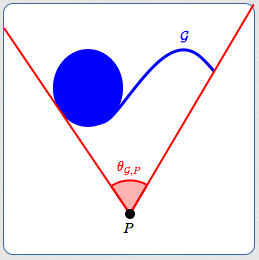
Let $\,P\,$ be a point, in the same plane as $\,\mathcal G\,,$ such that $\,P\,$ is not in $\,\mathcal G\,.$ For convenience, such a point is called an ‘external point’ (where ‘external’ means ‘external to $\,\mathcal G\,$’).

The symbol $\,\color{red}{\theta_{\mathcal G,P}}\,$ will be used to denote ‘the angle subtended by $\,\mathcal G\,$ at the external point $\,P\,$’. For convenience, the symbol $\,\theta_{\mathcal G,P}\,$ is used to denote both an angle (a geometric object) and the measure of this angle.

The symbol $\,\theta_{\mathcal G,P}\,,$ with its two subscripts, illuminates the two things needed in the definition of  ‘the angle subtended by a geometric object at an external point’:

• The first subscript, $\,\mathcal G\,,$ can be thought of as the object being viewed. In the eye chart example above, $\,\mathcal G\,$ would be a letter in the eye chart.
• The second subscript, $\,P\,,$ can be thought of as the external point from which $\,\mathcal G\,$ is being viewed. In the eye chart example above, $\,P\,$ would be the viewer's eye. The point $\,P\,$ is the vertex for the angle $\,\theta_{\mathcal G,P}\,.$

Roughly, $\,\theta_{\mathcal G,P}\,$ is the smallest angle, with vertex at $\,P\,,$ that ‘captures’ all of $\,\mathcal G\,.$

Motivation for Definition of $\,\theta_{\mathcal G,P}$

Here's the rough idea for defining $\,\theta_{\mathcal G,P}\,$:

• Extend a ray from $\,P\,$ that intersects $\,\mathcal{G}\,.$
• Sweep this ray in both directions to locate the two ‘edges’ of $\,\mathcal{G}\,.$
• Keep track of how far we sweep in both directions; add these measures together to get $\,\theta_{\mathcal G,P}\,.$

Humans are usually good at detecting the ‘edge’ or ‘boundary’ of geometric objects, but it's a bit tricky to define mathematically. (Topology can do it quite easily, but that's beyond the scope of this course.)

The problem is that a boundary point of an object might be part of the object, or not. (For example, in the interval $\,[3,4)\,,$ the number $\,4\,$ is a boundary point, but isn't in the interval.) Pay attention to how the least upper bound is used to resolve this issue in the definition below.

Now, let's make this idea mathematically precise:

Definition of $\,\theta_{\mathcal G,P}$

Step 1: Get an Intersecting Ray

Extend a ray from $\,\color{green}{P}\,$ that intersects $\,\color{green}{\mathcal G}\,.$ Since $\,\mathcal G\,$ is nonempty, such a ray exists. Call this the ‘reference ray’. The angles $\,\alpha\,$ and $\,\beta\,$ (defined below, each between $\,0^\circ\,$ and $\,360^\circ\,$) are both measured from the reference ray.

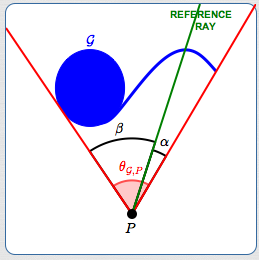
Step 2: Sweep the Ray Clockwise

Make a copy of the reference ray, and call it the ‘sweeping ray’. (The sweeping ray initially sits right on top of the reference ray.) Rotate the sweeping ray clockwise from the reference ray. Let $\,\theta_{\text{sweep}}\,$ denote the nonnegative angle between the reference and sweeping rays.

Step 3: Decide When to Stop Sweeping

As the sweeping ray rotates, it either intersects $\,\mathcal G\,,$ or not.

• If the sweeping ray intersects $\,\mathcal G\,$ continuously until $\,\theta_{\text{sweep}}\,$ reaches $\,360^\circ\,,$ then skip steps (4) and (5), and set $\,\theta_{\mathcal G,P} = 360^\circ\,.$
• Otherwise, stop the rotation when the sweeping ray does not intersect $\,\mathcal G\,,$ and define $\,\alpha\,$ to be the least upper bound of all angles $\,\theta_{\text{sweep}}\,$ such that the sweeping ray intersects $\,\mathcal G\,.$

Roughly, the angle $\,\alpha\,$ is used to capture one ‘edge’ of $\,\mathcal G\,$ (if an ‘edge’ exists).

Step 4: Sweep in the Other Direction

Repeat steps (2) and (3), except this time rotate counterclockwise.

• If the sweeping ray intersects $\,\mathcal G\,$ continuously until $\,\theta_{\text{sweep}}\,$ reaches $\,360^\circ\,,$ then set $\,\theta_{\mathcal G,P} = 360^\circ\,.$
• Otherwise, stop the rotation when the sweeping ray does not intersect $\,\mathcal G\,,$ and define $\,\beta\,$ to be the least upper bound of all angles $\,\theta_{\text{sweep}}\,$ such that the sweeping ray intersects $\,\mathcal G\,.$

Roughly, the angle $\,\beta\,$ is used to capture ‘the other edge’ of $\,\mathcal G\,.$

Step 5: Add the Sweep Angles

Define: $\,\theta_{\mathcal G,P} = \alpha + \beta$

Examples

In all these examples:

• The geometric object, $\,\mathcal G\,,$ is shown in blue
• The reference ray is shown in green
• The external point, $\,P\,,$ is shown in black
• The subtended angle $\,\theta_{\mathcal G,P}\,$ (when nonzero) is shown in red

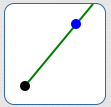
Point
$\alpha = 0^\circ\,,$ $\beta = 0^\circ$
$\theta_{\mathcal G, P} = 0^\circ$

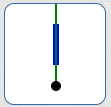
Line segment
$\alpha = 0^\circ\,,$ $\beta = 0^\circ$
$\theta_{\mathcal G, P} = 0^\circ$

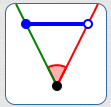
Line segment
$\alpha = 52^\circ\,,$ $\beta = 0^\circ$
$\theta_{\mathcal G, P} = 52^\circ$

When sweeping clockwise, $\,\theta_{\text{sweep}}\,$ takes on values in the interval $\,[0^\circ,52^\circ)\,$; the supremum is $\,52^\circ\,$

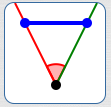
Line segment
$\alpha = 0^\circ\,,$ $\beta = 52^\circ$
$\theta_{\mathcal G, P} = 52^\circ$

When sweeping counterclockwise, $\,\theta_{\text{sweep}}\,$ takes on values in the interval $\,[0^\circ,52^\circ]\,$; the supremum is $\,52^\circ\,$

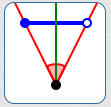
Line segment
$\alpha = 26^\circ\,,$ $\beta = 26^\circ$
$\theta_{\mathcal G, P} = 52^\circ$

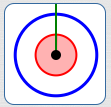
Circle
$\theta_{\mathcal G, P} = 360^\circ$

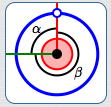
Punctured circle
$\alpha = 90^\circ\,,$ $\beta = 270^\circ$
$\theta_{\mathcal G, P} = 360^\circ$

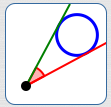
Circle
$\alpha = 33^\circ\,,$ $\beta = 0^\circ$
$\theta_{\mathcal G, P} = 33^\circ$

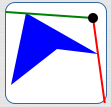
Filled polygon
$\alpha = 0^\circ\,,$ $\beta = 103^\circ$
$\theta_{\mathcal G, P} = 103^\circ$

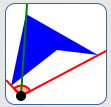
Filled polygon
$\alpha = 57^\circ\,,$ $\beta = 49^\circ$
$\theta_{\mathcal G, P} = 106^\circ$

Equivalent Definitions

When you communicate with others, you must agree on definitions. However, some things have more than one definition. Equivalent definitions can sometimes look quite different.

One definition may be easier to understand or easier to work with than another.

What makes two definitions equivalent? Roughly, they must produce exactly the same results. More precisely, for any object:

• If definition #1 yields a result, then definition #2 must yield the same result
• If definition #2 yields a result, then definition #1 must yield the same result

It's not always easy to see that two definitions are equivalent. Equivalence of definitions must be proved.

An equivalent definition of $\,\theta_{\mathcal G, P}\,$ is offered below. Given any nonempty path-connected geometric object in a plane and any external point, the same angle $\,\theta_{\mathcal G, P}\,$ will be found with both definitions.

The two definitions are similar. The equivalent definition doesn't require the concept of ‘least upper bound’. Instead, it relies on the fact that an interval has the same length regardless of its endpoints. That is, for all real numbers $\,a\,$ and $\,b\,$ with $\,a\le b\,,$ the intervals $\,(a,b)\,,$ $\,[a,b)\,,$ $\,(a,b]\,$ and $\,[a,b]\,$ all have length $\,b - a\,.$

Use whichever definition is easiest for you.

Using the original definition

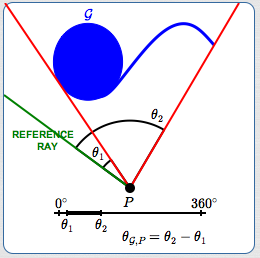
Using the equivalent definition

Equivalent Definition of $\,\theta_{\mathcal G, P}$

Let $\,\mathcal G\,$ be a nonempty path-connected geometric object in a plane. Let $\,P\,$ be a point, in the same plane as $\,\mathcal G\,,$ such that $\,P\,$ is not in $\,\mathcal G\,.$

Step 1: Get a Non-Intersecting Ray

Extend a ray from $\,P\,$ that does not intersect $\,\mathcal G\,$ (called the ‘reference ray’). If no such ray exists, then $\,\theta_{\mathcal G, P} = 360^\circ\,.$

Step 2: Sweep the Ray

Copy the reference ray, and call it the ‘sweeping ray’. (The sweeping ray initially sits right on top of the reference ray.) Rotate the sweeping ray clockwise (or counterclockwise) $\,360^\circ\,$ from the reference ray, marking (on a number line) all the angle measures for which the sweeping ray intersects $\,\mathcal G\,.$

Step 3: Get the Interval of Intersections

Since $\,\mathcal G\,$ is path-connected, step (2) yields a single interval. Define $\,\theta_{\mathcal G, P}\,$ to be the length of this interval.