Geometric Series (Finite and Infinite)
In an earlier lesson, geometric sequences were introduced. Recall that a sequence is just a list of numbers, separated by commas. When you sum (add together) the numbers in a geometric sequence, you get a geometric series. Sequences are lists; series are sums.
Also recall that summation notation gives a compact way to represent sums, when the terms exhibit some common pattern—like in geometric series.
Finite Geometric Series
Consider this finite geometric series:
$$ a + ar^1 + ar^2 + \cdots + ar^n $$The first term is $\,a\,,$ and you move from term-to-term by multiplying by $\,r\,.$ The final exponent is $\,n\,.$ This sum has $\,n+1\,$ terms. Of course, $\,ar^1 = ar\,$; the exponent of $\,1\,$ just adds clarity in counting the number of terms.
For example, if $\,a = 2\,,$ $\,r = 3\,,$ and $\,n = 7\,$ then the pattern $\,a + ar + ar^2 + \cdots + ar^n\,$ becomes:
$$ \begin{align} 2 + 2\cdot 3^1 + 2\cdot 3^2 + \cdots + 2\cdot 3^7 \end{align} $$If $\,n\,$ is large, then it's tedious to add up all these terms. The next formula comes to the rescue!
Let $\,a\,$ and $\,r\ne 1\,$ be real numbers, and let $\,n\,$ be a positive integer. Then:
$$ \begin{align} &a + ar + ar^2 + \cdots + ar^n\cr\cr &\qquad = a \cdot \frac{1 - r^{n+1}}{1 - r} \end{align} $$For example:
$$ \begin{align} &2 + 2\cdot 3^1 + 2\cdot 3^2 + \cdots + 2\cdot 3^7\cr\cr &\quad = \sum_{n=0}^7\ 2\cdot 3^n\ \ \text{(recall that $\,3^0 = 1\,$)}\cr\cr &\quad = 2\cdot\frac{1 - 3^8}{1 - 3}\cr\cr &\quad = 6560 \end{align} $$(Check this by adding them up the old-fashioned way!)
Derivation of Formula for the Sum of a Finite Geometric Series
Define:
$$ S_n := a + ar + ar^2 + \cdots + ar^n $$Multiplying both sides by $\,r\,$ gives:
$$ rS^n = ar + ar^2 + ar^3 + \cdots + ar^n + ar^{n+1} $$The formatting below helps to reveal the key step in the derivation:
| $S_n$ | $=$ | $a$ | $+$ | $\color{red}{ar}$ | $+$ | $\color{green}{ar^2}$ | $+$ | $\cdots$ | $+$ | $\color{orange}{ar^n}$ | ||
| $rS_n$ | $=$ | $\color{red}{ar}$ | $+$ | $\color{green}{ar^2}$ | $+$ | $\cdots$ | $+$ | $\color{orange}{ar^n}$ | $+$ | $ar^{n+1}$ |
Since almost all the terms cancel out:
$$ \color{blue}{S_n - rS_n} = a - ar^{n+1} \overset{\ \text{factor}\ }{=} a(1 - r^{n+1}) \tag{1} $$Also, simple factoring gives:
$$ \color{blue}{S_n - rS_n} = S_n(1 - r)\tag{2} $$Equating ($1$) and ($2$) gives
$$ S_n(1-r) = a(1 - r^{n+1}) $$so that, for $\,r\ne 1\,$:
$$ S_n = a\cdot\frac{1-r^{n+1}}{1-r} $$Infinite Geometric Series
With the finite geometric series summation formula in hand, we can now investigate the infinite geometric series:
$$ a + ar + ar^2 + ar^3 + \cdots $$First of all, be sure that you notice the difference between
$$\begin{gather} a + ar^1 + ar^2 + \cdots + ar^n\cr \text{(a finite geometric series)} \tag{F} \end{gather} $$and
$$ \begin{gather} a + ar + ar^2 + ar^3 + \color{red}{\cdots}\cr \text{(an infinite geometric series)} \tag{I} \end{gather} $$The finite series (F) (for ‘Finite’) STOPS. Indeed, there are exactly $\,n+1\,$ terms.
The infinite series (I) (for ‘Infinite’) DOES NOT STOP. There are an infinite number of terms. That lingering ‘$\,\color{red}{\cdots}\,$’ at the end indicates that the terms continue ad infinitum.
Of course, it makes perfectly good sense to add up a finite number of terms. But, what exactly does it mean to ‘add up an infinite number of terms’?
Spoiler: You can't add up an infinite number of terms. You can only add a finite number of terms. But ... Calculus limits come to the rescue! Keep reading!
Convergent versus Divergent Infinite Geometric Series
For motivation, let's consider four different ‘flavors’ of infinite geometric series. Each of these has $\,a = 1\,,$ but they have different values of $\,r\,$:
$$ \begin{align} &1 + 3^1 + 3^2 + 3^3 + \cdots\cr &\quad = 1 + 3 + 9 + 27 + \cdots \qquad (r = 3) \tag{D1}\cr\cr\cr &1 + (-3)^1 + (-3)^2 + (-3)^3 + \cdots\cr &\quad = 1 - 3 + 9 - 27 + \cdots \qquad (r = -3) \tag{D2}\cr\cr\cr &1 + (\frac 13)^1 + (\frac 13)^2 + (\frac 13)^3 + \cdots\cr &\quad = 1 + \frac 13 + \frac 19 + \frac 1{27} + \cdots \qquad (r = \frac 13) \tag{C1}\cr\cr\cr &1 + (-\frac 13)^1 + (-\frac 13)^2 + (-\frac 13)^3 + \cdots\cr &\quad = 1 - \frac13 + \frac 19 - \frac1{27} + \cdots \qquad (r = -\frac 13) \tag{C2} \end{align} $$Partial Sums for an Infinite Series
Since only a finite number of terms can be added, to explore infinite series, we investigate their partial sums. Let's start with a couple definitions:
Let
$$ a_1 + a_2 + a_3 + \cdots $$be an infinite series.
The $\,n^{\text{th}}\,$ partial sum of this series, denoted by $\,S_n\,,$ is the sum of the first $\,n\,$ terms of the series:
$$ S_n = a_1 + a_2 + a_3 + \cdots + a_n $$In other words, the $\,n^{\text{th}}\,$ partial sum of an infinite series is a finite approximation, formed by adding up the first $\,n\,$ terms.
The sequence of partial sums is used to analyze convergence of an infinite series:
Let
$$ a_1 + a_2 + a_3 + \cdots $$be an infinite series with partial sums:
$$ S_n = a_1 + a_2 + a_3 + \cdots + a_n $$If
$$ \lim_{n\rightarrow\infty} S_n = L $$for some real number $\,L\,,$ then the infinite series is said to converge to $\,L\,.$
If the limit does not exist (or is infinite), then the infinite series is said to diverge.
But—you say—we haven't studied limits of sequences! Good news: the ideas in Limits should give you all the understanding you need, as follows:
Under what condition(s) is the following sentence true?
$$ \lim_{n\rightarrow\infty} S_n = L $$- (least precise) As $\,n\,$ gets bigger and bigger (goes to $\,\infty\,$), then $\,S_n\,$ gets closer and closer to $\,L\,.$ That is: as you add up more and more terms in the series, the partial sum gets closer and closer to $\,L\,.$
- (more precise) We can get $\,S_n\,$ as close to $\,L\,$ as desired, by requiring that $\,n\,$ be sufficiently large. That is: we can get the partial sum as close to $\,L\,$ as we want, by just adding up enough terms in the series.
- (most precise) $$ \begin{gather} \lim_{n\rightarrow\infty} S_n = L\cr \iff\cr \text{for every } \epsilon \gt 0\cr \text{there exists } M\gt 0\cr \text{such that whenever } N\gt M\cr \text{we have } |S_N - L| \lt \epsilon \end{gather} $$
Don't worry if that ‘most precise’ sentence isn't accessible to you (right now). The first two explanations, together with the four examples that follow, is enough at present!
Note: When working with the infinite geometric series (I), we have:
$$ S_n = a + ar + ar^2 + \cdots + ar^{n-1} $$There are $\,n-1\,$ terms containing $\,r\,,$ and the initial term $\,a\,.$ Just be aware of this: $\,S_n\,$ actually ends with the term $\,ar^{n-1}\,$.
$r = 3\,$: The Sum Blows Up As You Add More and More Terms
Let's look at the first few partial sums for the series (D1):
$$ \begin{align} &1 + 3^1 + 3^2 + 3^3 + \cdots\cr &\quad = 1 + 3 + 9 + 27 + \cdots \qquad (r = 3) \tag{D1} \end{align} $$| $n$ | $S_n$ | $=$ | (sum of $\,n\,$ terms) | $=$ | (first $\,n\,$ terms, added up) |
| $1$ | $S_1$ | $=$ | $1$ | $=$ | $1$ |
| $2$ | $S_2$ | $=$ | $1 + 3$ | $=$ | $4$ |
| $3$ | $S_3$ | $=$ | $1 + 3 + 3^2$ | $=$ | $13$ |
| $4$ | $S_4$ | $=$ | $1 + 3 + 3^2 + 3^3$ | $=$ | $40$ |
Here are the first ten partial sums:
| $1$ |
| $4$ |
| $13$ |
| $40$ |
| $121$ |
| $364$ |
| $1093$ |
| $3280$ |
| $9841$ |
| $29524$ |
Here's a graph of those first ten partial sums:
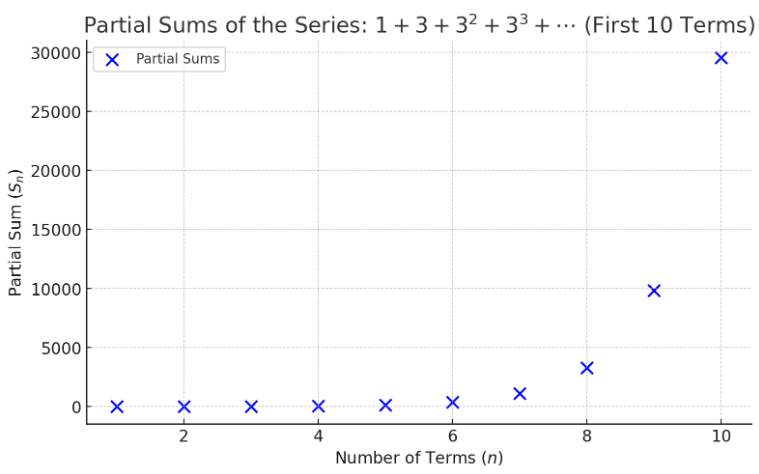
The first five data points $\,(1,1)\,,$ $\,(2,4)\,,$ $\,(3,13)\,,$ $\,(4,40)\,,$ and $\,(5,121)\,$ all ‘look like’ they're at the same height on the graph, since they're so close relative to the scale on the $y$-axis.
It's super clear what's happening to the list of partial sums: as you add on more and more terms, the partial sum is blowing up. In particular, the sequence of partial sums is not getting close to any particular real number. It's just getting bigger and bigger. This is an example of a divergent infinite geometric series (hence the label D1).
$r = -3\,$: The Sum Oscillates Wildly As You Add More and More Terms
Let's look at the first few partial sums for the series (D2):
$$ \begin{align} &1 - 3^1 + 3^2 - 3^3 + \cdots\cr &\quad = 1 - 3 + 9 - 27 + \cdots \qquad (r = -3) \tag{D2} \end{align} $$| $n$ | $S_n$ | $=$ | (sum of $\,n\,$ terms) | $=$ | (first $\,n\,$ terms, added up) |
| $1$ | $S_1$ | $=$ | $1$ | $=$ | $1$ |
| $2$ | $S_2$ | $=$ | $1 - 3$ | $=$ | $-2$ |
| $3$ | $S_3$ | $=$ | $1 - 3 + 3^2$ | $=$ | $7$ |
| $4$ | $S_4$ | $=$ | $1 - 3 + 3^2 - 3^3$ | $=$ | $-20$ |
Here are the first ten partial sums:
| $1$ |
| $-2$ |
| $7$ |
| $-20$ |
| $61$ |
| $-182$ |
| $547$ |
| $-1640$ |
| $4921$ |
| $-14762$ |
Here's a graph of those first ten partial sums:
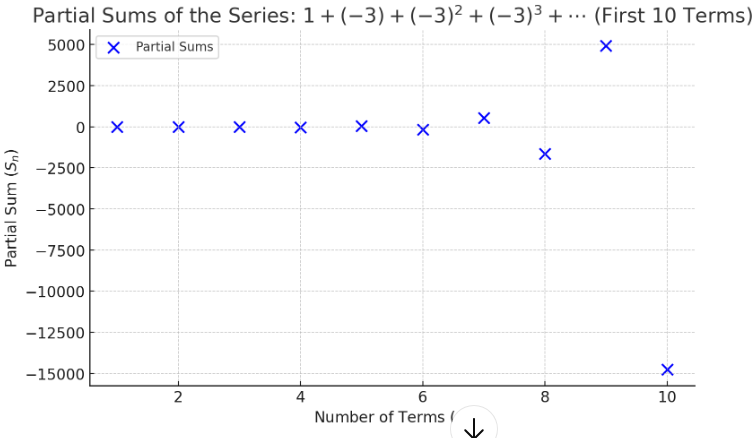
The first five data points do oscillate, but it's hard to see with the scale on the $y$-axis. But the pattern is clear: the partial sums are positive, negative, positive, negative $\,\ldots\,$ getting bigger and bigger with each oscillation. That's pretty wild oscillation: the partial sums are definitely not getting close to any particular real number! This is a second example of a divergent infinite geometric series (hence the label D2).
$r = \frac 13\,$: The Sum Gets Closer and Closer to $\,1.5\,$ As You Add More and More Terms
Let's look at the first few partial sums for the series (C1):
$$ \begin{align} &1 + (\frac 13)^1 + (\frac 13)^2 + (\frac 13)^3 + \cdots\cr &\quad = 1 + \frac 13 + \frac 19 + \frac1{27} + \cdots \qquad (r = \frac 13) \tag{C1} \end{align} $$| $n$ | $S_n$ | $=$ | (sum of $\,n\,$ terms) | $=$ | (first $\,n\,$ terms, added up) |
| $1$ | $S_1$ | $=$ | $1$ | $=$ | $1$ |
| $2$ | $S_2$ | $=$ | $1 + \frac 13$ | $\approx$ | $1.333$ |
| $3$ | $S_3$ | $=$ | $1 + \frac13 + \frac19$ | $\approx$ | $1.444$ |
| $4$ | $S_4$ | $=$ | $1 + \frac13 + \frac19 + \frac1{27}$ | $\approx$ | $1.481$ |
Here are the first ten (approximate) partial sums:
| $1$ |
| $1.333333$ |
| $1.444444$ |
| $1.481481$ |
| $1.493827$ |
| $1.497942$ |
| $1.499314$ |
| $1.499771$ |
| $1.499924$ |
| $1.499975$ |
Here's a graph of those first ten partial sums:
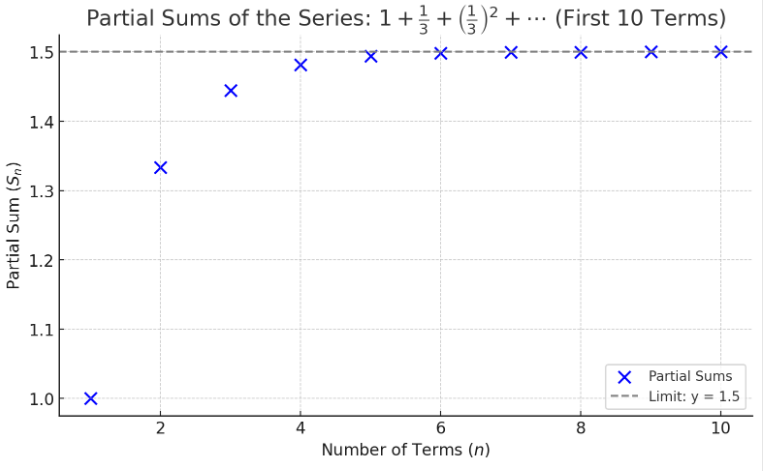
The partial sums are very quickly getting close to $\,1.5\,,$ coming in from below. The scale on the $y$-axis makes it look like the last few points have actually reached $\,1.5\,,$ but they haven't: they're just getting really close.
Indeed, by adding up enough terms, we can get as close to $\,1.5\,$ as we want! This is an example of a convergent infinite geometric series (hence the label C1). We say that the infinite series (C1) converges to $\,1.5\,.$
$r = -\frac 13\,$: The Sum Gets Closer and Closer to $\,0.75\,$ As You Add More and More Terms
Let's look at the first few partial sums for the series (C2):
$$ \begin{align} &1 + (-\frac 13)^1 + (-\frac 13)^2 + (-\frac 13)^3 + \cdots\cr &\quad = 1 - \frac 13 + \frac 19 - \frac1{27} + \cdots \qquad (r = -\frac 13) \tag{C2} \end{align} $$| $n$ | $S_n$ | $=$ | (sum of $\,n\,$ terms) | $=$ | (first $\,n\,$ terms, added up) |
| $1$ | $S_1$ | $=$ | $1$ | $=$ | $1$ |
| $2$ | $S_2$ | $=$ | $1 - \frac 13$ | $\approx$ | $0.666667$ |
| $3$ | $S_3$ | $=$ | $1 - \frac13 + \frac19$ | $\approx$ | $0.777778$ |
| $4$ | $S_4$ | $=$ | $1 - \frac13 + \frac19 - \frac1{27}$ | $\approx$ | $0.740741$ |
Here are the first ten (approximate) partial sums:
| $1$ |
| $0.666667$ |
| $0.777778$ |
| $0.740741$ |
| $0.753086$ |
| $0.749074$ |
| $0.750343$ |
| $0.749885$ |
| $0.750015$ |
| $0.749992$ |
Here's a graph of those first ten partial sums:
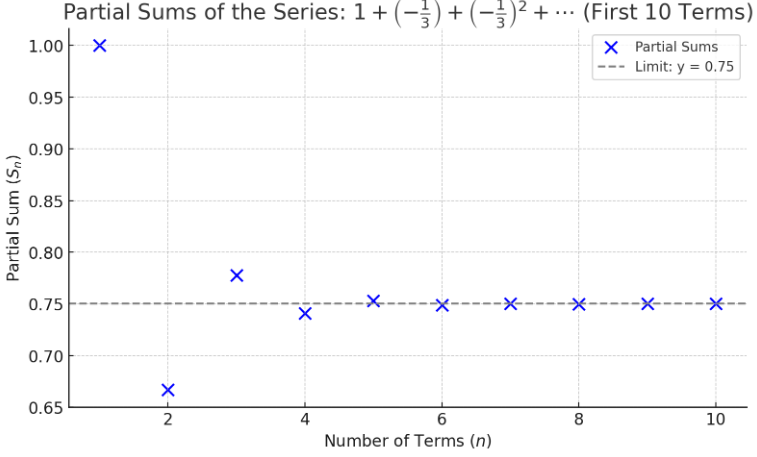
The partial sums are getting close to $\,0.75\,$: from above, then below, above, below $\,\ldots\,$ getting closer on each oscillation. The scale on the $y$-axis makes it look like the last few points have actually reached $\,0.75\,,$ but they haven't: they're just getting really close.
Indeed, by adding up enough terms, we can get as close to $\,0.75\,$ as we want! This is an example of a convergent infinite geometric series (hence the label C2). We say that the infinite series (C2) converges to $\,0.75\,.$
Formula for the Sum of an Infinite Geometric Series
What we've seen is that infinite geometric series sometimes converge, and sometimes diverge. Good news: it's easy to determine convergence/divergence, and it's easy to find the limiting value for a convergent series!
Let an infinite geometric series have first term $\, a \,$ and common ratio $\, r \,.$
Then, the infinite geometric series
$$ a + ar + ar^2 + ar^3 + \cdots \tag{I} $$converges if and only if $\, |r| < 1 \,,$ and in that case, the sum is:
$$ \sum_{n=0}^{\infty} ar^n = \frac{a}{1 - r}\ \ \ \ \ (\text{for } |r|\lt 1\,) $$If $\,|r| \geq 1\,,$ then the series diverges.
Note that $\,|r|\lt 1\,$ means $\,-1 \lt r \lt 1\,$: that is, $\,r\,$ is (strictly) between $\,-1\,$ and $\,1\,$.
Derivation of Formula for the Sum of an Infinite Geometric Series
The sum of the first $\,n\,$ terms of a finite geometric series is:
$$ S_n = a + ar + ar^2 + \cdots + ar^{n-1} = \dfrac{a(1 - r^n)}{1 - r}\,, \ \ \ \ \text{for } r \ne 1 $$If $\,|r|\lt 1\,$ then $\,r^n \to 0\,$ as $\,n \to \infty\,.$ So:
$$ \begin{align} &\lim_{n \to \infty} S_n \cr\cr &\qquad = \lim_{n \to \infty} \frac{a(1 - r^n)}{1 - r}\cr\cr &\qquad = \frac{a}{1 - r} \end{align} $$This is desired result. For $\,|r|\lt 1\,,$ the infinite geometric series (I) converges to $\,\frac a{1-r}\,.$ Informally, we say that ‘the sum of the infinite geometric series is $\,\frac a{1-r}\,.$’
Examples
Letting $\,a = 1\,$ and $\,r = \frac 13\,,$ we have:
$$ \begin{align} &1 + \frac 13 + (\frac 13)^2 + \cdots\cr\cr &\qquad = \frac{1}{1-\frac 13} \cr\cr &\qquad = \frac 32\cr\cr &\qquad = 1.5 \end{align} $$Letting $\,a = 1\,$ and $\,r = -\frac 13\,,$ we have:
$$ \begin{align} &1 + (-\frac 13) + (-\frac 13)^2 + \cdots\cr\cr &\qquad = \frac{1}{1-(-\frac 13)} \cr\cr &\qquad = \frac 1{4/3}\cr\cr &\qquad = \frac 34\cr\cr &\qquad = 0.75 \end{align} $$