Basic Derivative Information: Summary and Review
This lesson reviews and summarizes basic derivative information.
Derivatives Give Slope Information
The derivative of a function $\,f\,$ is a (new) function that gives the slopes of the tangent lines to the graph of $\,f\,.$
Derivatives give slope information.
Remember that (when they exist) tangent lines capture the direction you're moving as you travel along a curve .
Prime Notation for the Derivative
Using prime notation, the derivative of $\,f\,$ is named $\,f'\,.$ The function $\,f'\,$ is read aloud as ‘$\,f\,$ prime’.
Notice that $\,f\,$ is a function, and $\,f'\,$ is also a function. Usually (but not always!) the function $\,f'\,$ is different from the function $\,f\,.$
The function $\,f'\,$ gives the slopes of the tangent lines to the graph of $\,f\,.$
Here is a simple example to illustrate the derivative concept and prime notation:
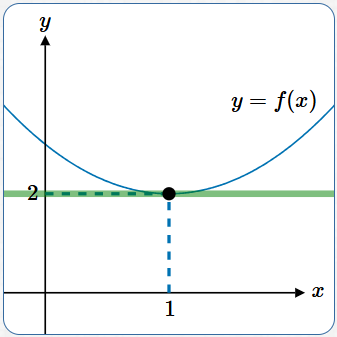
$f(x) = (x-1)^2 + 2$
Function rule that generates the graph;
a parabola with vertex $\,(1,2)$
$f(1) = (1-1)^2 + 2 = 2$
The point $\,(1,2)\,$ lies on the graph of $\,f$
Derivative information at a point:
$$f'(1) = 0$$Labeling the parts:
$$ \overbrace{f'}^{\text{slope of tangent line}} \underbrace{(1)}_{\text{when $x$ is $1$}}\ \ \overbrace{= 0}^{\text{is zero}} $$
The slope of the tangent line (shown in green),
when $\,x = 1\,,$ is zero (horizontal line).
The function $\,f'\,$ gives slope information!
As you travel along the curve (going from left to right), at the instant that you pass through the point $\,(1,2)\,,$ you're moving horizontally!
The $\,\frac{d}{dx}\,$ Operator for Differentiation
The $\,\frac{d}{dx}\,$ operator is an instruction to ‘take the derivative with respect to $\,x\,$ of whatever comes next’. You can read ‘$\,\frac{d}{dx}\,$’ as ‘dee dee x’ .
For example, $\,\frac{d}{dx}(x^2)\,$ denotes the derivative with respect to $\,x\,$ of $\,x^2\,.$
You can read ‘$\,\frac{d}{dx}(x^2)\,$’ as ‘dee dee x of x squared’ .
Similarly, $\,\frac{d}{dt}(t^2)\,$ denotes the derivative with respect to $\,t\,$ of $\,t^2\,.$
The $\,\frac d{dx}\,$ operator is particularly useful when differentiating a function that has not been given a name.
If a function has a name (like $\,f\,$) then the prime notation for the derivative ($\,f'\,$) is usually easier.
If you're differentiating a function that uses $\,x\,$ as its input variable, then use $\,\frac{d}{dx}\,$ to request its derivative. If a function uses $\,t\,$ to represent the input, then use $\,\frac{d}{dt}\,$ to request its derivative (and so on).
If there is no confusion about the function that $\,\frac{d}{dx}\,$ is acting on, then the parentheses that hold the function to be differentiated may be dropped.
For example, you can write $\,\frac d{dx} x^2\,$ (no parentheses) instead of $\,\frac d{dx}(x^2)\,$ (with parentheses).
Equivalent Characterization of Differentiability
If a function $\,f\,$ is differentiable at $\,x\,,$ then there is a non-vertical tangent line to the graph of $\,f\,$ at the point $\,\big(x,f(x)\bigr)\,.$
Also, if there is a non-vertical tangent line to the graph of $\,f\,$ at the point $\,\big(x,f(x)\bigr)\,,$ then the function $\,f\,$ is differentiable at $\,x\,.$
Thus:
$f\,$ is
differentiable
at $\,x$
is equivalent to
there is a non-vertical tangent line
to the graph of
$\,f\,$
at the point
$\,\bigl(x,f(x)\bigr)$
$f'(x)\,$ is a Number That Gives the Slope of a Tangent Line
The function $\,f'\,,$ evaluated at $\,x\,,$ is denoted by $\,f'(x)\,.$
$f'(x)\,$ is read aloud as ‘$f\,$ prime of $\,x\,$’.
$f'(x)\,$ is an expression. When $\,f'(x)\,$ exists, then it is a number.
The number $\,f'(x)\,$ is the derivative of $\,f\,$ at $\,x\,.$
The number $\,f'(x)\,$ gives the slope of the (non-vertical) tangent line to the graph of $\,f\,$ at the point $\,\bigl(x,f(x)\bigr)\,.$
$f'\,$ is a Function; $\,f'(x)\,$ is a Number
Be careful:
-
$f'\,$ is a function. The function $\,f'\,$ is called the derivative of $\,f\,.$
The function $\,f'\,$ might have a smaller domain than $\,f\,.$ Why?
Answer:
The function $\,f'\,$ gives the slopes of non-vertical tangent lines to the graph of $\,f\,.$
Does the graph of $\,f\,$ have any vertical tangent lines? Then, $\,f\,$ isn't differentiable there.
Or, are there places where $\,f\,$ doesn't have a tangent line (like at a kink or a break)? Then, $\,f\,$ isn't differentiable there.
- $f'(x)\,$ (when it exists) is a number. It is the derivative of $\,f\,$ evaluated at $\,x\,.$ The number $\,f'(x)\,$ gives the slope of the tangent line to the graph of $\,f\,$ at the point $\,(x,f(x))\,.$
If You're Worried About Differentiability at an Isolated Point ...
... then you're beyond the level of this Calculus course. (Think about pursuing a career in mathematics!)
When we talk about a function being differentiable at a point, we're assuming it's not an isolated point.
If you don't know what this is all about—just laugh and move on!
Conditions for a Function $\,f\,$ to be Differentiable at $\,x$
For $\,f\,$ to be differentiable at $\,x\,,$ all the following requirements must be met:
- $x\,$ must be in the domain of $\,f\,,$ so that the point $\,(x,f(x))\,$ exists
- There must be a tangent line to the curve at $\,(x,f(x))\,.$ When it exists, this tangent line captures the ‘direction you're moving’ as you walk along the curve.
- The tangent line must be non-vertical, so that it has a slope. Recall that a vertical line has no slope.
Every Important Calculus Idea is Defined in Terms of a Limit
Every important calculus idea is defined in terms of a limit. As an example, the derivative is defined in terms of a limit—keep reading!
The Definition of Derivative
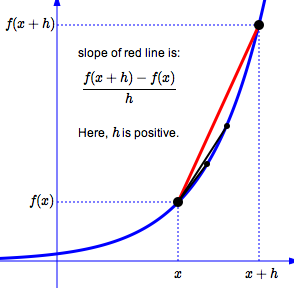
Here is the definition of $\,f'(x)\,.$ (Note that it's defined in terms of a limit!) As long as the limit exists, then:
$$f'(x) := \lim_{h\rightarrow 0} \frac{f(x+h) - f(x)}{h}$$Recall that ‘$\,:=\,$’ means ‘equals, by definition’.
Understanding the Expression that Appears in the Definition of Derivative
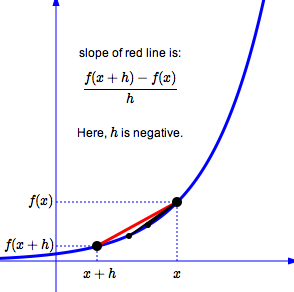
The expression
$$\frac{f(x+h) - f(x)}{h}$$gives the slope of the line between $\,\bigl(x,f(x)\bigr)\,$ and a (nearby) point $\,\bigl(x+h,f(x+h)\bigr)\,.$
Checking that this is indeed true:
$$ \begin{align} &\text{slope of line through}\cr &\bigl(x,f(x)\bigr) \text{ and } \bigl(x+h\ ,\ f(x+h)\bigr) \cr\cr &\qquad = \frac{y_2 - y_1}{x_2 - x_1}\cr\cr &\qquad = \frac{f(x+h)-f(x)}{(x+h)-x}\cr\cr &\qquad = \frac{f(x+h)-f(x)}h \end{align} $$(Notice that $\,x\,$ cancels out in the denominator.)
By taking the limit as $\,h\,$ approaches $\,0\,,$ the point $\,\bigl(x+h,f(x+h)\bigr)\,$ is ‘slid’ closer and closer to the original point $\,\bigl(x,f(x)\bigr)\,.$ Notice that as $\,h\,$ gets closer to zero, $\,x + h\,$ gets closer to $\,x\,.$
The definition of derivative solves the essential problem in finding the slope of a tangent line: usually, we only know one point on a tangent line. But, we need two points to compute a slope!
How is this problem solved? First, get the point where we want the tangent line: this is the point $\,(x,f(x))\,.$ Then, get a nearby point: this is the point $\,(x+h\,,\,f(x+h))\,.$ Slide the nearby point closer and closer by making $\,h\,$ smaller and smaller!
Equivalent Characterizations of ‘$\,f\,$ is Differentiable at $\,x\,$’
In summary, the following are equivalent for a number $\,x\,$ in the domain of $\,f\,$:
- $f\,$ is differentiable at $\,x$
- $f'(x)\,$ exists
- $\displaystyle\lim_{h\rightarrow 0}\frac{f(x+h)-f(x)}h\,$ exists
- There is a non-vertical tangent line to the graph of $\,f\,$ at the point $\,\bigl(x,f(x)\bigr)$
What if the Limit that Appears in the Definition of Derivative Doesn't Exist?
If the limit
$$\lim_{h\rightarrow 0} \frac{f(x+h) - f(x)}{h} $$doesn't exist, then we say that ‘$\,f\,$ is not differentiable at $\,x\,$’ or ‘$\,f'(x)\,$ does not exist’ . The phrase ‘does not exist’ is often abbreviated as DNE.
Equivalent Characterizations of ‘$\,f\,$ is Not Differentiable at $\,x\,$’
The following are equivalent for a number $\,x\,$ in the domain of $\,f\,$:
- $f\,$ is not differentiable at $\,x$
- $\,f'(x)\,$ does not exist (DNE)
- $\displaystyle\lim_{h\rightarrow 0}\frac{f(x+h)-f(x)}h\,$ does not exist
- There is not a non-vertical tangent line to the graph of $\,f\,$ at the point $\,(x,f(x))\,.$
The Definition of Derivative is Tedious to Use
The definition of derivative is tedious/
There must be a better way to find $\,f'(x)\,,$ rather than having to use the (limit) definition of derivative! There is! Start learning the Basic Differentiation Shortcuts here.