Multiplying Matrices

You may want to review:

Matrix multiplication is very different from matrix addition and subtraction.

You do not multiply corresponding entries: in particular, $\,[\,2\ \ 3\,]\,$ times $\,[\,4\ \ 5\,]\,$ is not Not NOT $\,[\,8\ \ 15\,]\,$!

Indeed, we'll see that these two matrices aren't even ‘compatible’ for matrix multiplication.

At first glance, the definition of matrix multiplication may seem strange and complicated. However, it is defined in a way that makes it perfect for working with systems of equations.

The example below may help you to understand why multiplication of matrices is defined the way it is.

Example (A Motivation For Matrix Multiplication)

The students in a large high school (grades $\,9\,$ through $\,12\,$) get there in a variety of ways: by bike, by bus, and by car.

The percentage of students using different modes of transportation is summarized on the left below. For example, $\,25\%\,$ of $\,9^{\text{th}}\,$ grade students travel to school by bike; $\,50\%\,$ of $\,12^{\text{th}}\,$ grade students travel to school by car.

The total number of male and female students in each grade is summarized in the table on the top right. For example, there are $\,110\,$ male $\,9^{\text{th}}\,$ grade students; there are $\,80\,$ female $\,12^{\text{th}}\,$ grade students.

					GENDER	Male	Female
					$\,9^{\text{th}}\,$	$110$	$105$
					$\,10^{\text{th}}\,$	$100$	$95$
					$\,11^{\text{th}}\,$	$95$	$90$
					$\,12^{\text{th}}\,$	$85$	$80$
MODES OF TRANSPORTATION	$\,9^{\text{th}}\,$	$\,10^{\text{th}}\,$	$\,11^{\text{th}}\,$	$\,12^{\text{th}}\,$
bike	$25\%$	$20\%$	$15\%$	$10\%$		$\begin{align}&0.25(110)\,+\, 0.20(100)\cr &\quad +\, 0.15(95)\,+\, 0.10(85)\cr &\quad = 70\end{align}$	$\begin{align}&0.25(105)\,+\, 0.20(95)\cr &\quad +\, 0.15(90)\,+\, 0.10(80)\cr &\quad = 67\end{align}$
bus	$55\%$	$65\%$	$55\%$	$40\%$		$\begin{align} &0.55(110)\,+\, 0.65(100)\cr &\quad +\, 0.55(95) \,+\, 0.40(85)\cr &\quad = 212\end{align}$	$\begin{align} &0.55(105)\,+\, 0.65(95)\cr &\quad +\, 0.55(90) \,+\, 0.40(80)\cr &\quad = 201\end{align}$
car	$20\%$	$15\%$	$30\%$	$50\%$		$\begin{align} &0.20(110) \,+\, 0.15(100)\cr &\quad +\, 0.30(95)\,+\, 0.50(85)\cr &\quad= 108\end{align}$	$\begin{align} &0.20(105) \,+\, 0.15(95)\cr &\quad +\, 0.30(90)\,+\, 0.50(80)\cr &\quad= 102\end{align}$

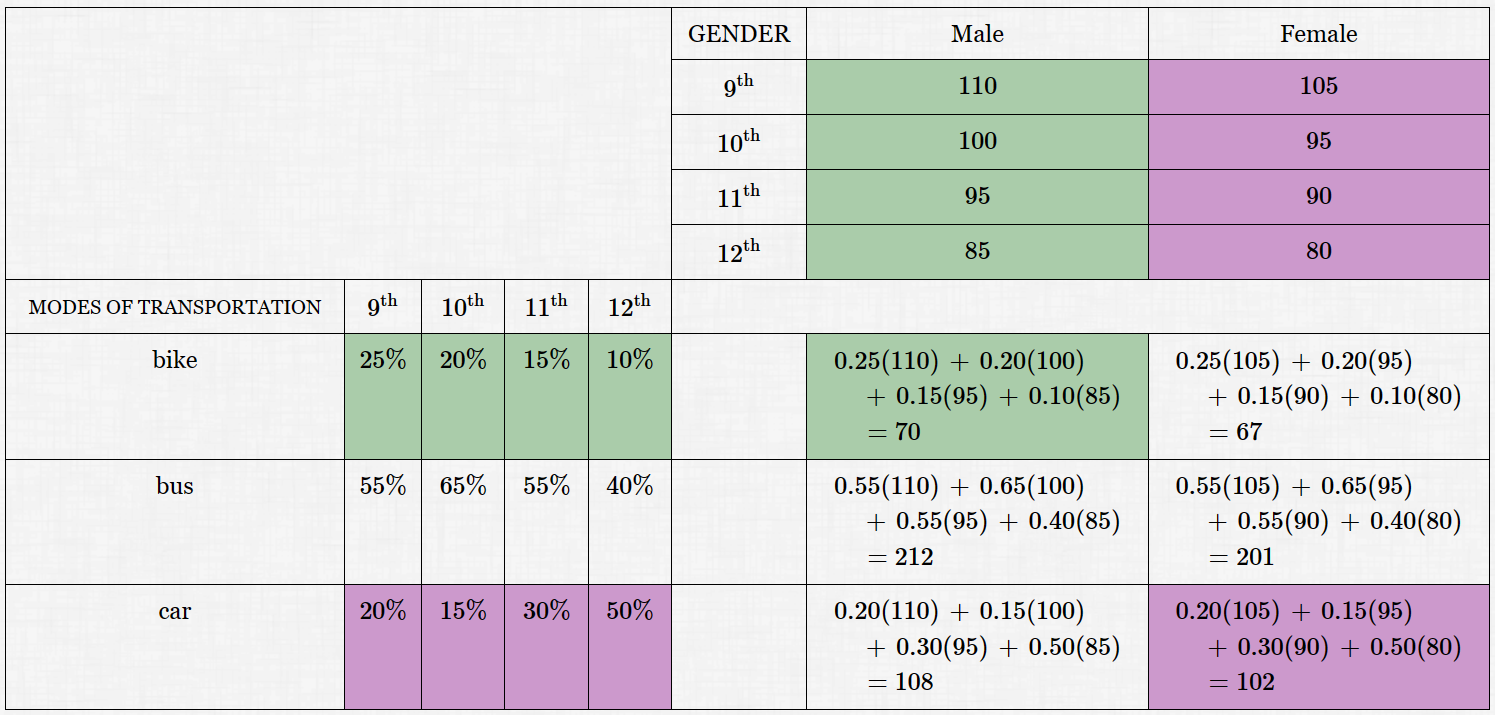
The following observations are critical:

The column labels of the ‘Modes of Transportation’ matrix ($\,9^{\text{th}}\,,$ $\,10^{\text{th}}\,,$ etc.) are the same as the row labels of the ‘Gender’ matrix.

In particular, there are the same number of columns in the ‘Modes’ matrix as there are rows in the ‘Gender’ matrix.
Look at the green entries above:
The ‘bike’ percentages (a row in the ‘Modes’ matrix) combine with the ‘male’ numbers (a column in the ‘Gender’ matrix) to give the total number of males who bike to school.

The computation is a sum of the products of corresponding entries.
Look at the purple entries above:
The ‘car’ percentages (a row in the ‘Modes’ matrix) combine with the ‘female’ numbers (a column in the ‘Gender’ matrix) to give the total number of females who go to school by car.

The computation is a sum of the products of corresponding entries.

Now strip away the labels, record the percentages as decimals, and suppress the computations.

Put the ‘Modes’ matrix in green and the ‘Gender’ matrix in purple.

The product of these two matrices is shown in white.

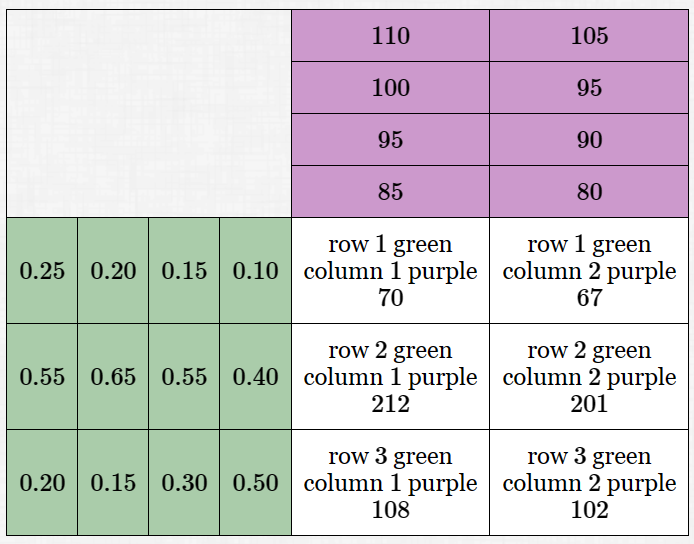
matrix multiplication example; no labels, commputations suppressed

Here is the most conventional display of this product of matrices:

$$ \begin{align} &\begin{bmatrix} 0.25 & 0.20 & 0.15 & 0.10 \cr 0.55 & 0.65 & 0.55 & 0.40 \cr 0.20 & 0.15 & 0.30 & 0.50 \end{bmatrix} \ \begin{bmatrix} 110 & 105 \cr 100 & 95 \cr 95 & 90 \cr 85 & 80 \cr \end{bmatrix}\cr &\qquad =\ \begin{bmatrix} 70 & 67 \cr 212 & 201 \cr 108 & 102 \end{bmatrix} \end{align} $$

Thus, we have:

DEFINITION matrix multiplication

Suppose that $\,A\,$ is an $\,m\times n\,$ matrix and $\,B\,$ is an $\,n\times p\,$ matrix.

(In particular, the number of columns in $\,A\,$ is the same as the number of rows in $\,B\,.$)

Then, the product $\,P:=AB\,$ is defined, and has size $\,m\times p\,.$

To find $\,p_{ij}\,$ (the element in row $\,i\,$ and column $\,j\,$ of the matrix $\,P\ $):

take row $\,i\,$ from matrix $\,A\,$;
take column $\,j\,$ from matrix $\,B\,$;
form the sum of the products of corresponding entries.

That is, if the numbers in the row from $\,A\,$ (left-to-right) are $\,a_1, a_2,\ldots, a_n\,,$ and the numbers in the column from $\,B\,$ (top-to-bottom) are $\ b_1, b_2,\ldots, b_n\,,$ then:

$$ \cssId{s56}{p_{ij} = a_1b_1 + a_2b_2 + \cdots + a_nb_n} $$

Notice how easy it is to organize systems of equations in matrix form with this definition! Check that the system

$$ \cssId{s59}{\begin{align} 2x-3y &=5\cr x+7y &=4 \end{align}} $$

has the following matrix representation:

$$ \cssId{s61}{\overset{\text{coefficient matrix}}{\overbrace{ \begin{bmatrix} 2 & -3\cr 1 & 7\cr \end{bmatrix}}}} \ \cssId{s62}{\underset{\text{variable matrix}}{\underbrace{ \begin{bmatrix} x\cr y \end{bmatrix}}}} \cssId{s63}{\ =\ \begin{bmatrix} 5 \cr 4 \end{bmatrix}} $$

Then, after additional tools for working with matrices are developed, the system can be easily solved using matrix methods.

				$110$	$105$
				$100$	$95$
				$95$	$90$
				$85$	$80$
$0.25$	$0.20$	$0.15$	$0.10$	row $1$ green column $1$ purple $70$	row $1$ green column $2$ purple $67$
$0.55$	$0.65$	$0.55$	$0.40$	row $2$ green column $1$ purple $212$	row $2$ green column $2$ purple $201$
$0.20$	$0.15$	$0.30$	$0.50$	row $3$ green column $1$ purple $108$	row $3$ green column $2$ purple $102$