There are two basic views of logarithms that you should know:
First, we need to get past the sometimes confusing notation used with logarithms,
which can make things seem harder than they really are.
Then, we talk about the ideas behind logarithms.
Logarithms are Numbers with Ugly Names
Logarithms (commonly shortened to just logs) are just numbers.
Part of the problem is that—well—they have ugly names, like:
$$
\cssId{s15}{\log_2{8}} \qquad \qquad \qquad \qquad
\cssId{s16}{\log_3{9}} \qquad \qquad \qquad \qquad
\cssId{s17}{\ln{\text{e}}} \qquad \qquad \qquad \qquad
\cssId{s18}{\log{100}}
$$
You need to learn how to read these numbers aloud,
and you need to understand the property that each of these numbers satisfies.
|
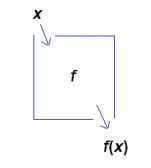
First of all, recall function notation: if the name of a function is $\,f\,$, and the input to the function is $\,x\,$, then the unique corresponding output is called $\,f(x)\,$ (which is read as ‘$\,f\,$ of $\,x\,$’.) |
|
Look at the function boxes below.
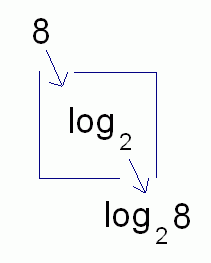
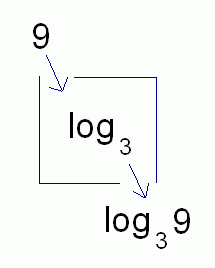
Notice that $\,\log_2\,$
(read aloud as log base $\,2\,$ )
is the name of a function!
Also, $\,\log_3\,$
(read aloud as log base $\,3\,$ )
is the name of a function!
The number $\,\log_2 8\,$ is the output from the function $\,\log_2\,$ when the input is $\,8\,$.
The number $\,\log_3 9\,$ is the output from the function $\,\log_3\,$ when the input is $\,9\,$.
 |
 |
So,
$\ \log_2 8\ $ and $\ \log_3 9\ $ are just outputs from functions named (respectively) $\,\log_2\,$ and $\,\log_3\,$.
Where are the parentheses that usually go around the input when using function notation?
Why aren't we writing $\,\log_2(8)\,$ and $\,\log_3(9)\,$?
There is a convention in mathematics about functions that have more than one letter to their name
(like $\,\log_2\,$ or $\log_3\,$):
if there's no confusion about the order of operations,
then you can DROP the parentheses used to ‘hold’ the input.
That is, it is conventional to write $\ \log_2 8\ $ instead of $\ \log_2(8)\ $.
The function $\,f\,$ has only one letter;
you would never shorten $\,f(x)\,$ to $\,fx\,$,
because this could be confused with multiplication.
However, when the function name is familiar
and has more than one letter, then there's no potential for confusion.
You read $\ \log_2 8\ $ aloud using normal function notation:
log base $\,2\,$ of $\ 8\,$.
(Notice the word of which denotes the function acting on the input.)
It's very important that you understand that
$\ \log_2 8\,$ is the output from the function
$\ \log_2\,$ when the input is $\ 8\ $.
It's so important that we'll put it in a centered box:
$\,\log_2 8\,$ is the output from the function
$\,\log_2\,$ when the input is $\,8\,$
Two Special Logarithms
You'll learn more about the bases of logarithms (the little number in the subscript position) later on.
For now, however, you should know that there are two important logarithms that are given special names.
If you have a calculator with two buttons that look like this, then here's what that ‘LOG’ and ‘LN’ mean:
COMMON LOGARITHM
log base ten
The function $\ \log_{10}\ $
(log base $10$)
is called the common logarithm or common log.
Some people write just $\ \log\ $ (no base) instead of the more cumbersome $\ \log_{10}\ $.
With this abbreviation:
Some people write just $\ \log\ $ (no base) instead of the more cumbersome $\ \log_{10}\ $.
With this abbreviation:
- when you see the function $\ \log\ $ with no base, then the base is actually $\,10\,$
- the number $\ \log x\ $ can be read aloud as ‘the common log of ex’
NATURAL LOGARITHM
log base e
Let $\ \text{e}\ $ denote the irrational number $\ \text{e}\approx 2.72\ $.
The function $\ \log_{\text{e}}\ $ (log base $\text{e}$) is called the natural logarithm or natural log.
Some people write just $\ \ln\ $ instead of the more cumbersome $\ \log_{\text{e}}\ $.
When you see the function $\ \ln\,$, you should recognize it as the logarithm with base $\ \text{e}\ $.
The number $\ \ln x\ $ can be read aloud as ‘the natural log of ex’.
Memory device: the letters ‘l n’, in reverse order, are ‘n l’, for ‘natural log’.
The function $\ \log_{\text{e}}\ $ (log base $\text{e}$) is called the natural logarithm or natural log.
Some people write just $\ \ln\ $ instead of the more cumbersome $\ \log_{\text{e}}\ $.
When you see the function $\ \ln\,$, you should recognize it as the logarithm with base $\ \text{e}\ $.
The number $\ \ln x\ $ can be read aloud as ‘the natural log of ex’.
Memory device: the letters ‘l n’, in reverse order, are ‘n l’, for ‘natural log’.
The common log and the natural log are the only two logs that appear on many handheld calculators.
Caution: different people use different notation
Some academic disciplines use the natural log a lot, but the common log not so much.
These disciplines often use $\,\log\,$ to mean log base e, instead of log base ten.
Be sure to check what notation is being used whenever you start communicating with someone new.
For example, if you go to wolframalpha.com
and type in log 100 then here's what you'll see:
Here, WolframAlpha is assuming that you want the natural log.
If you want the common log instead, you need to click ‘the base 10 logarithm’ link.
(By the way, you get very different results. Try it!)
Logarithms are Exponents
| Question: | So, what exactly is the number $\,\log_2 8\,$? |
| Answer: | It is the power that $\,2\,$ must be raised to, to get $\,8\,$! |
When you're asked to find
$\,\log_2 8\,$, these words should form in your head:
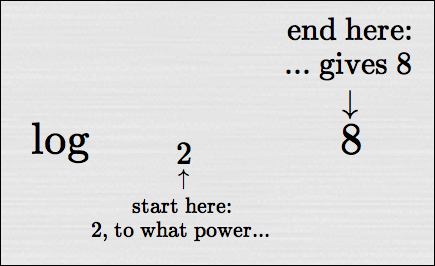
You dip down, and start with the $\,2\,$.
Then you say ‘to what power ... ’
Finish with ‘... gives $\,8\,$’?
The POWER is the ANSWER.
That's why we say that ‘logarithms are exponents’ or ‘logarithms are powers’.
In this example, the answer is $\,3\,$,
since $\,2\,$ to the power $\,3\,$ gives $\,8\,$:
$\,2^3 = 8\,$.
Thus, $\,\log_2 8 = 3\,$.
For fun, head up to wolframalpha.com and type in:
log base 2 of 8
Voila!
It is convenient to think of making the ‘circle’ shown below:
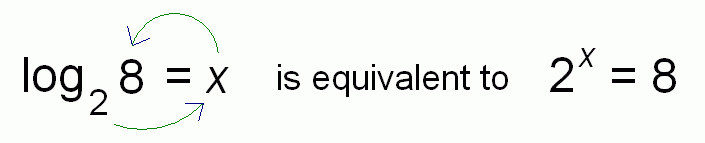
Since $\,2^3 = 8\,$,
it follows that $\,\log_2 8 = 3\,$.
Read ‘$\,\log_2 8 = 3\,$’ aloud as ‘log base $\,2\,$ of $\,8\,$ is $\,3\,$’.
Thus, we have the KEY IDEA:
or
LOGARITHMS ARE POWERS
EXAMPLES:
What is $\,\log_3 9\,$?
It is the power that $\,3\,$ must be raised to, to get $\,9\,$.
Since $\,3^2 = 9\,$, it follows that $\,\log_3 9 = 2\,$.
Since $\,3^2 = 9\,$, it follows that $\,\log_3 9 = 2\,$.
What is $\,\log 1000\,$?
It is the power that $\,10\,$ must be raised to, to get $\,1000\,$.
Since $\,10^3 = 1000\,$, it follows that $\,\log 1000 = 3\,$.
Since $\,10^3 = 1000\,$, it follows that $\,\log 1000 = 3\,$.
What is $\,\ln \sqrt{\text{e}}\,$?
It is the power that $\,\text{e}\,$ must be raised to, to get $\,\sqrt{\text{e}}\,$.
Since $\,{\text{e}}^{1/2} = \sqrt{\text{e}}\,$, it follows that $\,\ln\sqrt{\text{e}} = \frac12\,$.
Since $\,{\text{e}}^{1/2} = \sqrt{\text{e}}\,$, it follows that $\,\ln\sqrt{\text{e}} = \frac12\,$.
What is $\,\log_{57} \frac{1}{57}\,$?
It is the power that $\,57\,$ must be raised to, to get $\,\frac{1}{57}\,$.
Since $\,57^{-1} = \frac{1}{57}\,$, it follows that $\,\log_{57} \frac{1}{57} = -1\,$.
Since $\,57^{-1} = \frac{1}{57}\,$, it follows that $\,\log_{57} \frac{1}{57} = -1\,$.
What is $\,\log_{24} 1\,$?
It is the power that $\,24\,$ must be raised to, to get $\,1\,$.
Since $\,24^0 = 1\,$, it follows that $\,\log_{24} 1 = 0\,$.
Since $\,24^0 = 1\,$, it follows that $\,\log_{24} 1 = 0\,$.
EXAMPLE:
Question:
Estimate the following logarithm: $\log_3 7$
That is, find two positive integers between which the logarithm lies.
Give a reason to support your answer.
Estimate the following logarithm: $\log_3 7$
That is, find two positive integers between which the logarithm lies.
Give a reason to support your answer.
Solution:
We need the power that $\,3\,$ must be raised to, to get $\,7\,$.
Since $\,3^1\,$ is only $\,3\,$ (and we want $\,7\,$), the power $\,1\,$ isn't big enough.
Since $\,3^2\,$ is $\,9\,$ (and we want $\,7\,$), the power $\,2\,$ is too big.
Thus, the power we really want is somewhere between $\,1\,$ and $\,2\,$.
We can say it briefly like this:
Since $\,3^1 = 3\,$ and $\,3^2 = 9\,$, $\,\log_3 7\,$ lies between $\,1\,$ and $\,2\,$.
We need the power that $\,3\,$ must be raised to, to get $\,7\,$.
Since $\,3^1\,$ is only $\,3\,$ (and we want $\,7\,$), the power $\,1\,$ isn't big enough.
Since $\,3^2\,$ is $\,9\,$ (and we want $\,7\,$), the power $\,2\,$ is too big.
Thus, the power we really want is somewhere between $\,1\,$ and $\,2\,$.
We can say it briefly like this:
Since $\,3^1 = 3\,$ and $\,3^2 = 9\,$, $\,\log_3 7\,$ lies between $\,1\,$ and $\,2\,$.
Master the ideas from this section
by practicing the exercise at the bottom of this page.
When you're done practicing, move on to:
Properties of Logarithms
by practicing the exercise at the bottom of this page.
When you're done practicing, move on to:
Properties of Logarithms