Composition of Functions

Carol Fisher's Homepage
Algebra II Table of Contents

For this exercise, you need ♥ INTERNET EXPLORER 6.0 and above, with MathPlayer installed.♥

COMPOSITION OF FUNCTIONS

Jump right to the exercises!

Numbers can be "connected" to get new numbers: for example, 1+2=3 .
Indeed, addition ( + ) is a connective for numbers.

Sets can be "connected" to get new sets: for example, {1}∪ {2}={1 ,2} .
Indeed, the union operator ( ∪ ) is a connective for sets.

Functions can also be "connected" to get new functions:
the most important way to do this, called function composition, is the subject of this section.

First, some basic review.
A function is a rule that takes an input, does something to it, and gives a unique corresponding output.
If the function name is f , and the input name is x , then the unique corresponding output is called f(x) (which is read as " f of x ".)
Note that f and f(x) are different mathematical expressions:
f is the name of the function;
f(x) is the output from the function f when the input is x .

It is often helpful to think of a function as a "box".
You drop an input in the top, something happens to the input inside the box, and the output drops out the bottom.
The box is labeled with the name of the function.

You can explore this "function box" using GeoGebra
by clicking here:
Function Boxes and Function Notation
(Please be patient.
It may take a few minutes for GeoGebra to load.)

Constructing a Composition of Functions

To construct a composition of functions,
start by putting function boxes in sequence,
(i.e., one right after the other), as shown at right.

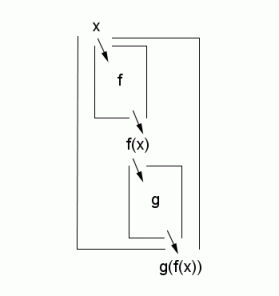
An input x is dropped into the first box (call it f ), giving the output f(x) .
This output f(x) is then dropped into the next box (call it g ), giving g(f(x )) .

Now, bundle these two functions f and g into a single, new, function:
this new function takes an input x and gives the output g(f(x )) .

What should this new function be named?
Certainly, the name should have something to do with both f and g .
It can't be named fg or gf , because these names are already taken to mean multiplication of outputs: for example, (fg)(x ) := f(x) g(x) .
In whatever name is decided upon, it might make sense to put the f before the g , since the function f gets to act first.
On the other hand, it might make sense to put the g first, since the g comes first when you look at the final output, g(f(x )) .
Decisions, decisions, decisions!

The name that was decided upon is...   g∘f
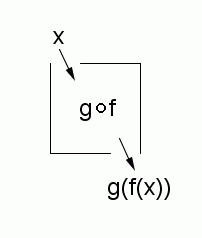
For us (high school mathematics and most others), the name chosen for this new function is g∘f ,
which is read aloud as   " g circle f  "    or    " g composed with f  ".
That is, by definition:
        (g∘f )(x)=g(f( x))
This sentence is read aloud as:
g circle f of x    equals     g of f of x
A function like g∘f is called a composite function.

Notice: g∘f is the name of our "new" function;
(g∘f )(x) (which equals g(f(x))  )
is the output from the function g∘f when the input is x .

BE CAREFUL!!
For the function g∘f ,
the function f acts FIRST,
and the function g acts LAST!

That is, in the output g(f(x)) ,
the function f is CLOSEST to the input x , so it acts first.

Practice with function composition

Let f(x)= x2 and g(x)= 2x .

Then,

(f∘g )(x)	:=	f(g(x))	definition of the function f∘g
	=	f(2x)	work from the inside to the outside; substitute 2x for g(x)
	=	(2x) 2	apply the squaring function, f , to 2x
	=	4x 2	simplify

Also,

(g∘f )(x)	:=	g(f(x))	definition of the function g∘f
	=	g(x2)	work from the inside to the outside; substitute x2 for f(x)
	=	2x 2	apply the "multiply by 2" function, g , to x 2

Notice that f(g(x)) is NOT equal to g(f(x)) .
In general, function composition is NOT commutative.

You can explore function composition using GeoGebra
by clicking here: Composition of Functions
(Please be patient. It may take a few minutes for GeoGebra to load.)

On this exercise, you will not key in your answer.
However, you can check to see if your answer is correct.

Algebra II Table of Contents

Please read my
TERMS OF USE