1.6 Sinusoids
The $\,x\,$ and $\,y\,$ coordinates of a point traveling around the unit circle $\,x^2+y^2 = 1\,$ exhibit periodic behavior: after each revolution, the coordinates of the point repeat.
This simple observation is the basis for the definitions of the important, periodic, sine and cosine functions.
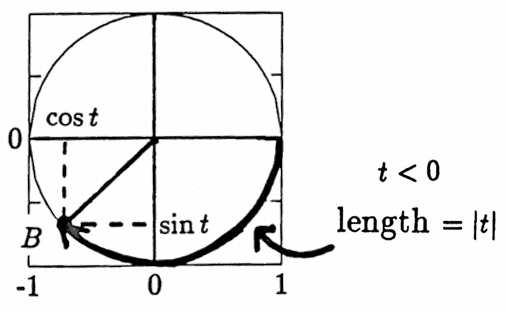
Let $\,t\,$ be any real number. Identify this real number $\,t\,$ with a point on the unit circle $\,C\, :\, x^2 + y^2 = 1\,,$ as follows:
- Start at the point $\,A := (1,0)\,.$
- If $\,t \ge 0\,,$ lay off an arc of length $\,t\,,$ in the counter-clockwise direction, on $\,C\,.$
- • If $\,t \lt 0\,,$ lay off an arc of length $\,|t|\,,$ in the clockwise direction, on $\,C\,.$
- Denote the point on $\,C\,$ at the terminal end of the arc by $\,B\,.$
In this manner, every real number $\,t\,$ is associated with a point $\,B\,$ on the unit circle.
Define the cosine function $\,\cos\,:\, \Bbb R\rightarrow [-1,1]\,$ by
$$ \cos t := \text{the $x$-coordinate of $\,B\,,$} $$and define the sine function $\,\sin\,:\,\Bbb R\rightarrow [-1,1]\,$ by:
$$ \sin t := \text{the $y$-coordinate of $\,B$} $$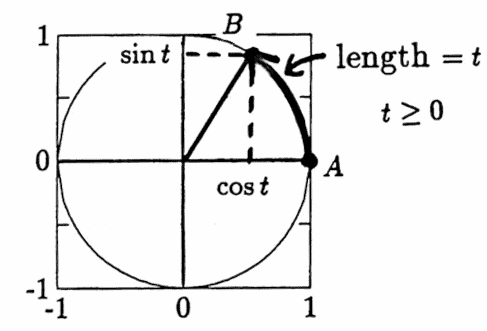
Example
Since the unit circle has circumference $\,2\pi\,,$ the real number $\,t = \frac\pi 2\,$ corresponds to the point $\,(0,1)\,$ on $\,C\,$; hence, $\,\sin \frac\pi 2 = 1\,$ and $\,\cos\frac\pi 2 = 0\,.$
The number $\,t = -\frac\pi 3\,$ corresponds to the point $\,\bigl(\frac 12,-\frac{\sqrt 3}2\bigr)\,$ on $\,C\,$; hence, $\,\sin(-\frac\pi 3) = -\frac{\sqrt 3}2\,$ and $\,\cos(-\frac\pi 3) = \frac 12\,.$
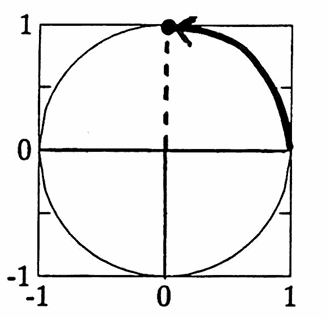
$t = \frac\pi 2$
$x$-coordinate $= 0$
$y$-coordinate $= 1$
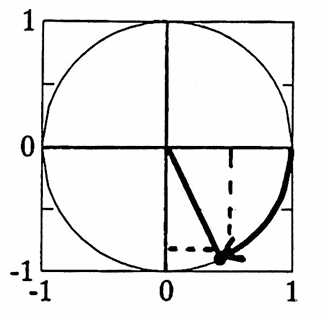
$t = -\frac\pi 3$
$x$-coordinate $= \frac 12$
$y$-coordinate $= -\frac{\sqrt 3}2$
The sine and cosine functions are graphed below. Since all real numbers $\,t\pm 2\pi k\,,\ k\in\Bbb Z\,,$ are associated with the same point on $\,C\,,$ one has:
$$ \begin{gather} \sin(t\pm 2\pi k) = \sin t\strut\cr \text{and}\strut\cr \cos(t\pm 2\pi k) = \cos t\strut\cr \forall\ \ t\in\Bbb R\,,\ k\in\Bbb Z\strut \end{gather} $$The fundamental period of both the sine and cosine functions is $\,2\pi\,.$
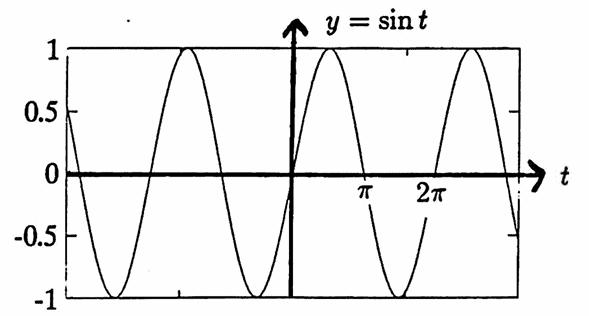
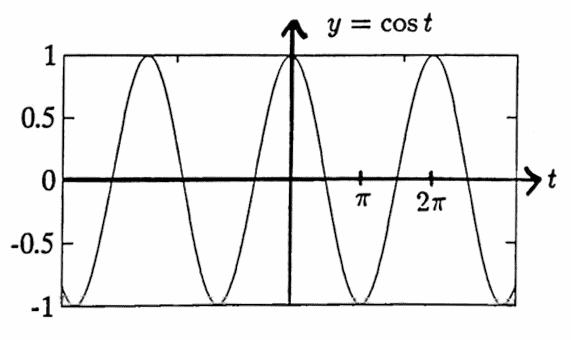
The process of identifying a real number $\,t\,$ with a point on the unit circle $\,C\,$ forms an angle in a natural way: use the positive $x$-axis as the beginning side of the angle, and the ray through the origin and $\,B\,$ as the terminal side of the angle.
By definition, the number $\,t\,$ is the radian measure of the angle thus formed. Therefore, the radian measure of an angle is a real number that represents a (signed) arc length on the unit circle. Note that $\,2\pi\,$ radians equals one complete revolution.
The degree measure of an angle is defined by dividing one complete revolution into $\,360\,$ equal parts. By definition:
$$ 1^\circ = \frac 1{360}\text{ revolution} $$Thus, $\,(2\pi\ \text{radians}) = 360^\circ\,.$
The grad measure of an angle is defined by dividing one complete revolution into $\,400\,$ equal parts. By definition:
$$ 1\text{ grad} = \frac 1{400}\text{ revolution} $$Thus, $\,400 \text{ grad} = 360^\circ = 2\pi\text{ radians}\,.$
Only the radian measure of an angle will be used in this dissertation.
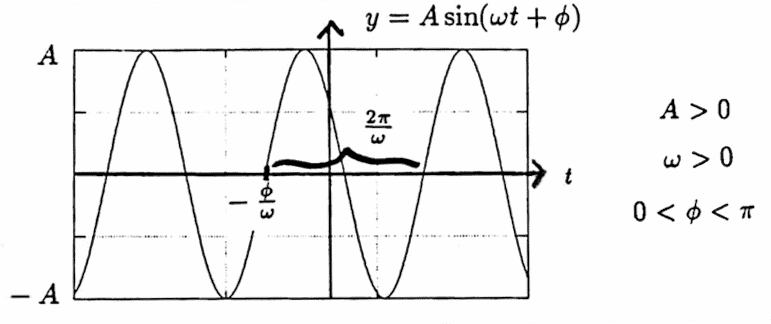
In this dissertation, a sinusoid is a function of the form
$$ a\sin(bt+c)\ \ \text{or}\ \ a\cos(bt+c)\,, $$for real numbers $\,a\,,$ $\,b\,$ and $\,c\,$ with $\,a\ne 0\,$ and $\,b\ne 0\,.$
Let $\,f(t)\,$ denote either $\,a\sin(bt+c)\,$ or $\,a\cos(bt+c)\,.$
The function $\,f\,$ makes one complete cycle as the argument of the sine or cosine goes from $\,0\,$ to $\,2\pi\,.$
Observe that $\,bt+c = 0\,$ when $\,t = -\frac cb\,$; and, $\,bt+c = 2\pi,$ when $\,t = \frac{2\pi-c}b\,.$ The resulting time interval has length $\,\bigl|\frac{2\pi-c}b - (-\frac cb)\big| = |\frac{2\pi}b|\,.$
The positive number $\,|\frac{2\pi}b|\,$ is the fundamental period of $\,f\,.$
The number $\,-\frac cb\,$ is the phase shift of $\,f\,.$
Observe that
$$a\sin(bt+c) = a\sin[b(t+\frac cb)]\,,$$so the curve $\,y = a\sin(bt)\,$ is shifted $\,\frac cb\,$ units to the left (if $\,\frac cb \ge 0\,$), or $\,\frac cb\,$ units to the right (if $\,\frac cb \lt 0\,$) to obtain the curve $\,y = a \sin(bt + c)\,.$ A similar statement holds for $\,a\cos(bt + c)\,$.
For all real numbers $\,t\,,$ $\,|f(t)| \le |a|\,,$ and on any interval of length $\,|\frac{2\pi}b|\,,$ the function $\,f\,$ takes on the values $\,\pm|a|\,.$
The number $\,|a|\,$ is the amplitude of $\,f\,.$
Two sinusoids are graphed below.
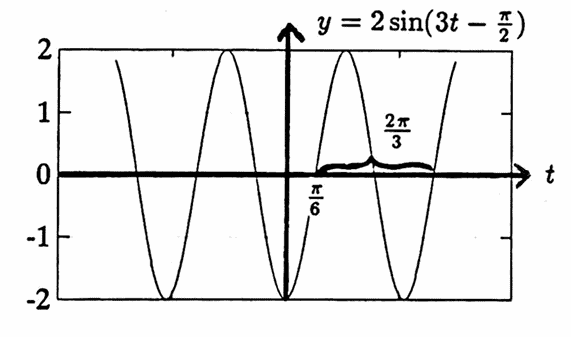
The representation of a sinusoid in the form $\,a\sin(bt+c)\,$ or $\,a\cos(bt + c)\,$ is not unique.
For example, for all real numbers $\,a\,,$ $\,b\,$ and $\,c\,$ with $\,a \ne 0\,$ and $\,b\ne 0\,,$ and for all integers $\,k\,$:
$$ \begin{gather} a\cos(bt+c) = a\sin(bt+c+\frac\pi 2)\cr\cr a\cos(bt+c) = -a\cos(bt+c\pm \pi)\cr\cr a\sin(bt+c) = -a\sin(-bt-c+2\pi k) \end{gather} $$However, appropriate restrictions can be placed on $\,a\,,$ $\,b\,$ and $\,c\,$ so that a unique representation is obtained. This is the content of the next proposition.
Every sinusoid has a unique representation in the form
$$ A\sin(\omega t + \phi) $$for $\,A\gt 0\,,$ $\,\omega\gt 0\,,$ and $\,-\pi \le\phi \lt \pi\,.$
Flow Chart for Proposition 1
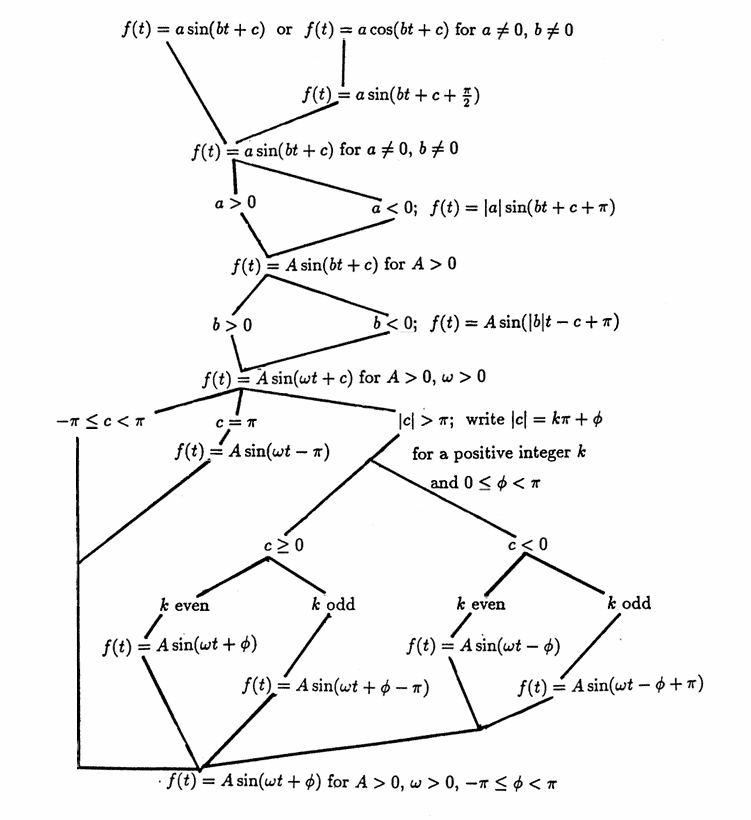
Proof: An Algorithm for Obtaining the Desired Form
For all real numbers $\,t\,$ and odd integers $\,k\,$:
$$ \begin{gather} \cos t = \sin(t + \frac\pi 2)\tag{1}\cr\cr \sin(t\pm k\pi) = -\sin t \tag{2} \end{gather} $$These facts are used freely in the following proof.
Let $\,f\,$ be any sinusoid. Thus, $\,f\,$ is of the form $\,f(t) = a\sin(bt+c)\,$ or $\,f(t) = a\cos(bt+c)\,$ for real numbers $\,a\,,$ $\,b\,$ and $\,c\,,$ with $\,a\ne 0\,$ and $\,b\ne 0\,.$
The algorithm presented next produces a representation of $\,f\,$ in the desired form. The previous flow chart summarizes this algorithm.
If $\,f(t) = a\cos(bt+c)\,,$ then:
$$ \begin{align} f(t) &= a\cos(bt+c)\cr &\overset{(1)}{=} a\sin(bt+c+\frac\pi 2) \end{align} $$This implies that $\,f\,$ can be written in the form $\,a\sin(bt+c)\,$ for $\,a\ne 0\,,$ $\,b\ne 0\,,$ and $\,c\in\Bbb R\,.$
If $\,a \lt 0\,,$ so that $\,a = -|a|\,,$ then:
$$ \begin{align} a\sin(bt+c) &= -|a|\sin(bt+c)\cr &\overset{(2)}{=} |a|\sin(bt+c+\pi) \end{align} $$Thus, $\,f\,$ is in the form $\,A \sin(bt + c)\,$ for $\,A \gt 0\,,$ $\,b\ne 0\,,$ and $\,c\in\Bbb R\,.$
If $\,b \lt 0\,,$ so that $\,b = -|b|\,,$ then use the fact that $\sin(-t) = -\sin t\,$ for all $\,t\,,$ so that:
$$ \begin{align} A\sin(bt+c) &= A\sin(-|b|t+c)\cr\cr &= A\sin[(-1)(|b|t-c)]\cr\cr &= -A\sin(|b|t-c)\cr\cr &\overset{(2)}{=} A\sin(|b|t - c + \pi) \end{align} $$As a result, $\,f\,$ can be put in the form $\,A\sin(\omega t + c)\,$ for $\,A\gt 0\,,$ $\,\omega \gt 0\,,$ and $\,c\in\Bbb R\,.$
If $\,c = \pi\,,$ then:
$$ A\sin(\omega t + \pi) = A\sin(\omega t - \pi) $$If $|c| \gt \pi\,,$ then $\,|c| = k\pi + \phi\,$ for $\,0\le\phi \lt \pi\,,$ for a positive integer $\,k\,.$
If $\,c \ge 0\,,$ so that $\,|c| = c\,,$ and $\,k\,$ is an even integer, then:
$$ \begin{align} A\sin(\omega t + c) &= A\sin(\omega t + |c|)\cr &= A\sin(\omega t + k\pi + \phi)\cr &= A\sin(\omega t + \phi) \end{align} $$If $\,c\ge 0\,$ and $\,k\,$ is odd, then:
$$ \begin{align} A\sin(\omega t + c) &= A\sin(\omega t + k\pi + \phi)\cr &\overset{(2)}{=} -A\sin(\omega t + \phi)\cr &\overset{(2)}{=} A\sin(\omega t + \phi - \pi) \end{align} $$Since $\,0 \le \phi \lt \pi\,,$ it follows that $\,-\pi \le (\phi - \pi) \lt 0\,.$
If $\,c \lt 0\,,$ so that $\,c = -|c|\,,$ and $\,k\,$ is even, then:
$$ \begin{align} A\sin(\omega t + c) &= A\sin(\omega t - |c|)\cr &= A\sin(\omega t - k\pi - \phi)\cr &= A\sin(\omega t - \phi) \end{align} $$And, if $\,c \lt 0\,$ and $\,k\,$ is odd, then:
$$ \begin{align} A\sin(\omega t + c) &= A\sin(\omega t - |c|)\cr &= A\sin(\omega t - k\pi - \phi)\cr &\overset{(2)}{=} -A\sin(\omega t - \phi)\cr &\overset{(2)}{=} A\sin(\omega t - \phi + \pi) \end{align} $$Since $\,0\le \phi \lt \pi\,,$ it follows that $\,0 \lt -\phi + \pi \le \pi\,.$ The only way that $\,-\phi + \pi\,$ can equal $\,\pi\,$ is if $\,\phi = 0\,,$ in which case $\,f(t) = A\sin(\omega t - k\pi)\,$ for an odd integer $\,k\,,$ so that $\,f(t) = A\sin(\omega t - \pi)\,.$
In all cases, $\,f\,$ has been written in the form $\,A\sin(\omega t + \phi)\,$ for $\,A \gt 0\,,$ $\,\omega \gt 0\,,$ and $\,-\pi \le \phi \lt \pi\,.$
Let $\,A_1\,,$ $\,A_2\,,$ $\,\omega_1\,$ and $\,\omega_2\,$ be positive, and let $\,\phi_1\,$ and $\,\phi_2\,$ be in the interval $\,[-\pi,\pi)\,.$ Two sinusoids with different amplitudes or frequencies cannot be equal, hence:
$$ \begin{align} &A_1\sin(\omega_1 t + \phi_1) = A_2\sin(\omega_2 t + \phi_2)\cr &\qquad\implies (A_1 = A_2) \text{ and } (\omega_1 = \omega_2) \end{align} $$If
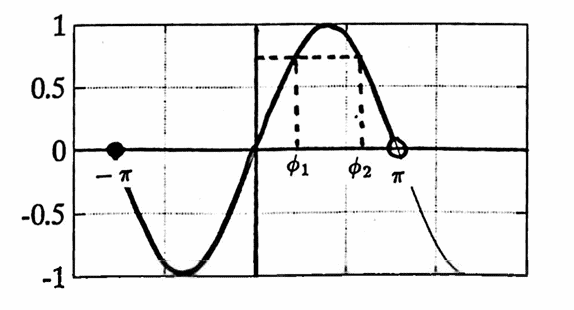
$$ A\sin(\omega t + \phi_1) = A\sin(\omega t + \phi_2)\ \forall\, t\,,\ -\pi\le \phi_i\lt \pi\,, $$then for $\,t = 0\,,$ one obtains $\,A\sin\phi_1 = A\sin\phi_2\,,$ from which $\,\sin\phi_1 = \sin\phi_2\,$; and for $\,t =\frac{\pi}{2\omega}\,,$ one obtains $\,\sin(\frac\pi 2 + \phi_1) = \sin(\frac\pi 2 + \phi_2)\,.$
An analysis of the sketch below illustrates that the only way that both $\,\sin\phi_1 = \sin\phi_2\,$ and $\,\sin(\frac\pi 2 + \phi_1) = \sin(\frac\pi 2 + \phi_2)\,$ can be true, when $\,\phi_1\,$ and $\,\phi_2\,$ are in the interval $\,[-\pi, \pi)\,,$ is for $\,\phi_1 = \phi_2\,.$ $\blacksquare$
Whenever the notation $\,A\sin(\omega t + \phi)\,$ is used in this dissertation, it is assumed that $\,A\gt 0\,,$ $\,\omega\gt 0\,,$ and $\,-\pi\le\phi\lt\pi\,.$
The word frequency is often used in the context of sinusoids for two different types of frequencies. To prevent any possible confusion with regard to this word, the following definitions and notation are set forth.
Suppose that a periodic function $\,g\,$ has fundamental period $\,P\,.$ Then, the function passes through all possible function values on any interval $\,[t,t+P)\,,$ and the function is said to have made one oscillation.
The cyclic frequency of $\,g\,$ is denoted by $\,f\,,$ and is defined by:
$$f := \frac 1P$$The radian frequency of $\,A\sin(\omega t + \phi)\,$ is the positive number $\,\omega\,.$
These definitions imply that cyclic frequency can be computed for any periodic function, whereas radian frequency can be computed only for sinusoids.
Note that cyclic frequency tells how many cycles the function makes in unit time.
Since the function $\,A\sin(\omega t + \phi)\,$ has fundamental period $\,\frac{2\pi}\omega\,,$ the relationship between radian frequency and cyclic frequency is given by $\,f = \frac 1{(2\pi/\omega)}\,,$ that is:
$$\omega = 2\pi f$$Whenever the variables $\,\omega\,$ and $\,f\,$ are used in the context of sinusoids, they will always denote radian and cyclic frequency, respectively.
Thus, many commonly-appearing sinusoids will take the form:
$$ \sin\omega t\ \ \text{ or }\ \ \sin 2\pi ft $$Note that
$$ \sin\frac{2\pi t}P = \sin 2\pi(\frac 1P)t $$has fundamental period $\,P\,.$
For the convenience of the reader, some important trigonometric identities are summarized next. For all real numbers $\,t\,,$ $\,\alpha\,,$ and $\,\beta\,$:
$$ \begin{gather} \sin(-t) = -\sin t\cr\cr \cos(-t) = \cos t\cr\cr \sin^2 t + \cos^2 t = 1 \end{gather} $$In the half-angle formulas, the correct choice of sign is determined by the location of the point on the unit circle associated with $\,t/2\,.$
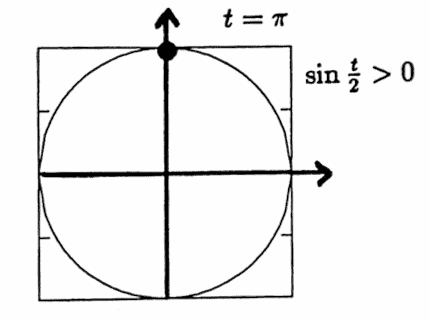
For example, letting $\,t = \pi\,,$
$$ \sin\frac\pi 2 = +\sqrt{\frac{1-\cos\pi}2} = 1\,, $$since the point determined by $\,t/2\,$ has a positive $y$-coordinate.
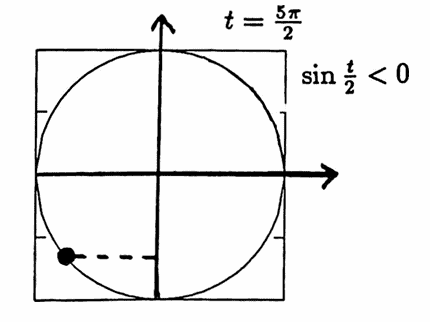
Letting $\,t = \frac{5\pi}2\,,$
$$ \begin{align} \sin\frac t2 &= \sin\frac{5\pi}4\cr\cr &= -\sqrt{\frac{1-\cos\frac{5\pi}2}2}\cr\cr &= -\frac 1{\sqrt{2}}\ , \end{align} $$since the point determined by $\,t/2\,$ has a negative $y$-coordinate.
The importance of sinusoids is largely due to the fact that any continuous periodic function can be well-approximated by a sum of sinusoids. The interested reader is referred to any real analysis text, say [Bar, 330-345], for proofs of the following classic results:
Let $\,g\,$ be a periodic real-valued function of one real variable, with fundamental period $\,P\,.$
The function $\,g\,$ is piecewise continuous on $\,\Bbb R\,$ if $\,g\,$ is defined and continuous on $\,\Bbb R\,,$ except possibly for a finite number of points $\,t_1,\ldots,t_n\,$ in any interval of length $\,P\,,$ at which $\,g\,$ has both left and right hand limits,
$$ \begin{gather} g(t_i^-) := \lim_{h\rightarrow0^+} g(t_i - h)\,,\cr\cr g(t_i^+) := \lim_{h\rightarrow0^+} g(t_i + h) \end{gather} $$where the notation $\,h\rightarrow 0^+\,$ means that $\,h\,$ approaches $\,0\,$ from the right-hand side.
Let $\,g\,$ be a periodic real-valued function of one real variable. Suppose that $\,g\,$ is piecewise continuous on $\,\Bbb R\,,$ and has fundamental period $\,P\,.$
The Fourier series of $\,g\,$ is the infinite sum
$$ \begin{gather} \frac{a_0}2 + \sum_{k=1}^\infty \bigl( a_k\cos\frac{2\pi kt}P + b_k\sin\frac{2\pi kt}P\bigr)\cr \text{(CFS)} \end{gather} $$where the Fourier coefficients $\,a_k\,$ and $\,b_k\,$ are given by the formulas:
$$ \begin{gather} a_k = \frac 2P\int_P g(t)\cos\frac{2\pi kt}P\,dt\,,\cr\cr b_k = \frac 2P\int_P g(t)\sin\frac{2\pi kt}P\,dt \end{gather} $$The notation $\,\int_P\,$ is used to mean that the integral may be evaluated over any interval of length $\,P\,.$
The label (CFS) stands for continuous Fourier series.
The requirement that $\,g\,$ be piecewise continuous guarantees that the integrals defining $\,a_k\,$ and $\,b_k\,$ exist.
Since $\,g\,$ has fundamental period $\,P\,,$ and the functions $\,\cos\frac{2\pi kt}P\,$ and $\,\sin\frac{2\pi kt}P\,$ have a period $\,P\,,$ the integrands in the integrals defining $\,a_k\,$ and $\,b_k\,$ have a period $\,P\,.$ This is what makes it possible to integrate over any interval of length $\,P\,.$
Any function $\,g\,$ defined on a finite interval $\,[a,b)\,$ can be extended periodically to $\,\Bbb R\,,$ as illustrated below.
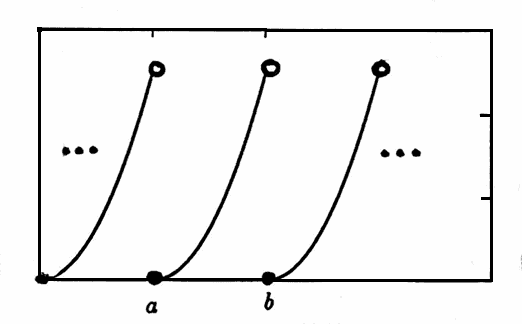
Note that the arguments of the sinusoids in the Fourier series are of the form
$$ \frac{2\pi kt}P = 2\pi(k\cdot\frac 1P)t\,, $$so that the cyclic frequencies are multiples of $\,\frac 1P\,.$ In this context, $\,P\,$ and $\,\frac 1P\,$ are called the fundamental period and fundamental (cyclic) frequency, respectively, of the series. The multiples of the frequencies are called the harmonics.
The next two theorems describe the relationship between the function $\,g\,$ and its Fourier series.
Let $\,g\,$ be a periodic real-valued function of one real variable. Suppose that $\,g\,$ is piecewise continuous on $\,\Bbb R\,,$ and has fundamental period $\,P\,.$
Suppose further that $\,g\,$ has right and left-hand derivatives at $\,c\in\Bbb R\,$; that is, both
$$ \begin{gather} \lim_{h\rightarrow 0^+} \frac{g(c+h) - g(c^+)}h\cr\cr \text{and}\cr\cr \lim_{h\rightarrow 0^+} \frac{g(c-h) - g(c^-)}h \end{gather} $$exist.
Then, the Fourier series for $\,g\,$ converges to $\,\frac 12\bigl( g(c^-) + g(c^+)\bigr)\,$ at $\,c\,.$
In particular, if $\,g\,$ is continuous at $\,c\,,$ then the Fourier series for $\,g\,$ at $\,c\,$ converges to $\,g(c)\,.$
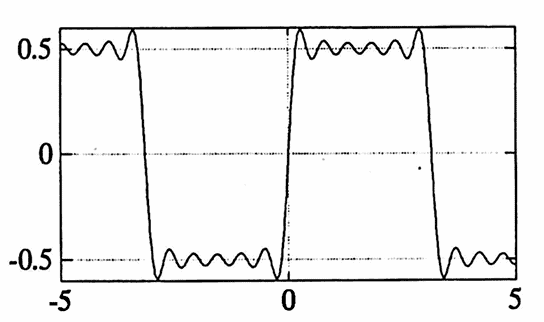
With only pointwise convergence, as guaranteed by the previous theorem, some undesirable types of behavior can occur. To illustrate what can ‘go wrong’, consider the function:
$$ g(t) = \begin{cases} -0.5 & \text{for}\ -\pi\lt t \lt 0\cr\cr 0.5 & \text{for}\ 0 \lt t \lt \pi \end{cases} $$Extend $\,g\,$ periodically to all of $\,\Bbb R\,,$ call this extension by the same name, and form its Fourier series. Observe that $\,g\,$ meets the hypotheses of the Pointwise Convergence Theorem.
Let $\,c\,$ be any number in the interval $\,(0,\pi)\,.$ Via pointwise convergence, the Fourier series for $\,g\,$ must converge to $\,g(c) = 0.5\,$ at $\,x = c\,.$
Therefore, if $\,\epsilon\,$ is any positive number, there exists a positive integer $\,N\,$ such that whenever $\,n \ge N\,,$
$$ \left| \left( \frac{a_0}2 + \sum_{k=1}^n a_k\cos\frac{2\pi kc}P + b_k\sin\frac{2\pi kc}P \right) - 0.5 \right| \le \epsilon\ , $$where the $\,a_k\,$ and $\,b_k\,$ are the Fourier coefficients.
Unfortunately, however, somewhere in the interval $\,(0,c)\,,$ the truncated Fourier series will always take on a value that overshoots $\,0.5\,$ by more than $\,0.089\,$; and that undershoots $\,0.5\,$ by more than $\,0.048\,$ [HamD, 107–109], as illustrated below.
This behavior, known as the Gibbs' phenomenon (after J. Willard Gibbs, who first publicized the effect but was not the first to publish it), is typical of the behavior of any truncated Fourier series near a jump discontinuity.
An understanding of this behavior will become important in Chapter 3, when designing mathematical filters.
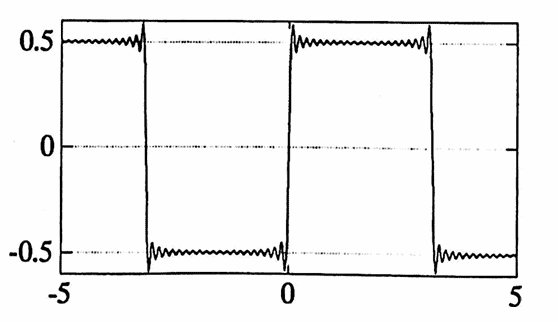
A much more desirable type of convergence is uniform convergence.
Roughly, a sequence of functions $\,(g_i)_{i=1}^\infty\,$ converges uniformly to $\,g\,$ if, given any $\epsilon$-envelope about $\,g\,,$ one can get all the functions $\,g_n\,$ from the list to lie entirely within this $\epsilon$-envelope, providing that $\,n\ge N\,$ for some sufficiently large positive integer $\,N\,.$
With slightly stronger hypotheses on $\,g\,,$ one can actually get the Fourier series of $\,g\,$ to converge uniformly to $\,g\,$:
Let $\,g\,$ be a periodic real-valued function of one real variable, defined on $\,\Bbb R\,.$ Suppose that $\,g\,$ is continuous with fundamental period $\,P\,,$ and suppose that the derivative $\,g'\,$ is piecewise continuous on $\,\Bbb R\,.$
Then, the Fourier series for $\,g\,$ converges uniformly to $\,g\,$ on $\,\Bbb R\,.$ That is, for every $\,\epsilon\gt 0\,,$ there exists a positive integer $\,N\,$ such that for all $\,n\ge N\,$ and for all $\,t\in\Bbb R\,$:
$$ \left| \left( \frac{a_0}2 + \sum_{k=1}^n a_k\cos\frac{2\pi kt}P + b_k\sin\frac{2\pi kt}P \right) - g(t) \right| \le \epsilon $$The formulas for the coefficients $\,a_k\,$ and $\,b_k\,$ of the Fourier series can be derived by:
- assuming that a series of the form (CFS) exists and represents $\,g\,$; $$ g(t) = \frac{a_0}2 + \sum_{k=1}^n \left(a_k\cos\frac{2\pi kt}P + b_k\sin\frac{2\pi kt}P\right) $$
- multiplying both sides of this equation by $\,\cos\frac{2\pi mt}P\,$ (or $\,\sin\frac{2\pi mt}P\,$) for a fixed integer $\,m\,$;
- integrating over one period; and
-
using the following orthogonality
properties of the sine and
cosine: for all positive integers $\,n\,$
and $\,m\,,$
$$
\begin{gather}
\int_P \cos\bigl(\frac{2\pi nt}P\bigr)
\cos\bigl(\frac{2\pi mt}P\bigr)\,dt
=
\cases{
0 & \text{if}\ n\ne m \cr
\frac P2 & \text{if}\ n = m
}
\cr\cr
\int_P \sin\bigl(\frac{2\pi nt}P\bigr)
\sin\bigl(\frac{2\pi mt}P\bigr)\,dt
=
\cases{
0 & \text{if}\ n\ne m \cr
\frac P2 & \text{if}\ n = m
}
\cr\cr
\int_P \sin\bigl(\frac{2\pi nt}P\bigr)
\cos\bigl(\frac{2\pi mt}P\bigr)\,dt
= 0 \ \ \forall\ n\,, m
\end{gather}
$$
These orthogonality properties cause most of the terms in the sum to vanish.
This same procedure will be followed in the derivation of the coefficients for the discrete Fourier series in Chapter 2.
The Fourier series also has the following desirable property:
[Weav, 113] Let $\,g\,$ be a periodic real-valued function of one real variable. Suppose that $\,g\,$ is piecewise continuous on $\,\Bbb R\,,$ and has fundamental period $\,P\,.$
If $\,g\,$ is approximated by any finite series of the form
$$ S_N(t) := \frac{a_0}2 + \sum_{k=1}^N \left( a_k\cos\frac{2\pi kt}P + b_k\sin\frac{2\pi kt}P \right) $$for real coefficients $\,a_k\,$ and $\,b_k\,,$ then the best approximation in terms of the mean-square error is obtained when the Fourier coefficients are used for $\,a_k\,$ and $\,b_k\,.$
That is, the mean-square error between $\,S_N\,$ and $\,g\,,$ defined by
$$ \int_P \bigl( g(t) - S_N(t)\bigr)^2\,dt\,, $$is minimized when $\,S_N\,$ is the $\,N^{\text{th}}\,$ partial sum of the Fourier series for $\,g\,.$
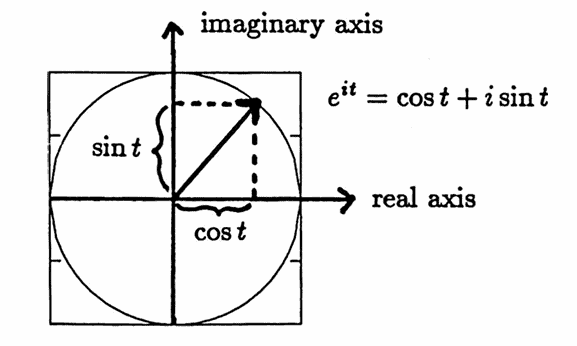
The complex exponential function is defined by
$$ e^{it} := \cos t + i\sin t\,, $$for all real numbers $\,t\,,$ and for $\,i := \sqrt{-1}\,.$ Thus, $\,e^{it}\,$ is a complex number, with real part equal to $\,\cos t\,,$ and imaginary part equal to $\,\sin t\,.$
The Complex Plane
Here are some important consequences of this definition. Using the identities $\,\cos(-t) = \cos t\,$ and $\,\sin(-t) = -\sin t\,,$ one obtains:
$$ \begin{gather} e^{it} = \cos t + i\sin t\tag{1}\cr e^{-it} = \cos t - i\sin t\tag{2} \end{gather} $$Adding $(1)$ and $(2),$ and dividing by $\,2\,,$ gives:
$$ \cos t = \frac{e^{it} + e^{-it}}2 $$That is, $\,e^{it} + e^{-it} = 2\cdot\text{Re}(e^{it})\,,$ where $\,\text{Re}(e^{it})\,$ denotes the real part of $\,e^{it}\,.$ The geometric interpretation of this identity is shown below.
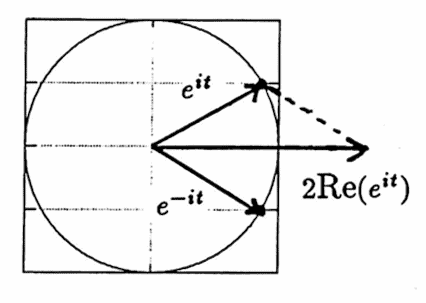
$e^{it} + e^{-it} = 2\cdot\text{Re}(e^{it})$
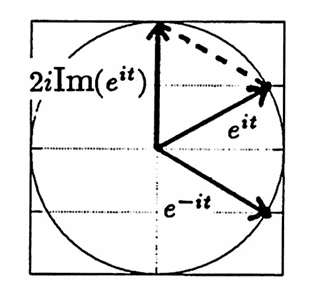
$e^{it} - e^{-it} = 2i\cdot\text{Im}(e^{it})$
Subtracting $(2)$ from $(1),$ and dividing by $\,2i\,,$ gives:
$$ \sin t = \frac{e^{it} - e^{-it}}{2i} $$That is, $\,e^{it} - e^{-it} = 2i\cdot\text{Im}(e^{it})\,,$ where $\,\text{Im}(e^{it})\,$ denotes the imaginary part of $\,e^{it}\,.$ The geometric interpretation of this identity is shown above.
The identity in the next proposition reflects an important property of equal-spaced sampling from the complex exponential function. This identity will become important when discussing the discrete Fourier series in Chapter 2.
Here's a geometric interpretation of the identity: let $\,N\,$ be a positive integer greater than $\,1\,,$ and let $\,k\,$ be a fixed integer between $\,1\,$ and $\,N - 1\,.$ Then, the complex numbers
$$ \begin{align} &1\,,\cr &e^{2\pi ki(\frac 1N)}\,,\cr &e^{2\pi ki(\frac 2N)}\,,\cr &e^{2\pi ki(\frac 3N)}\,,\cr &\vdots\ , \cr &e^{2\pi ki(\frac{N-1}N)}\,, \end{align} $$divide $\,2\pi k\,$ revolutions of the unit circle in the complex plane into $\,N\,$ equal arc lengths. When these complex numbers are summed, the result is $\,0\,.$ The result is illustrated below for two different combinations of $\,k\,$ and $\,N\,.$
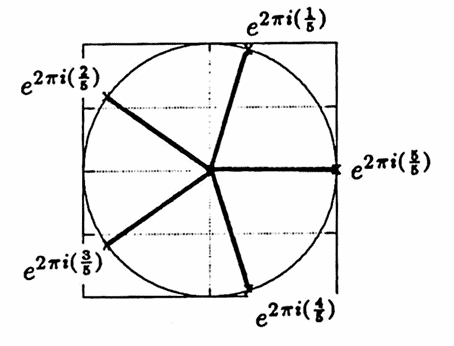 $$\begin{gather}
k = 1\cr
N = 5
\end{gather}
$$
$$\begin{gather}
k = 1\cr
N = 5
\end{gather}
$$
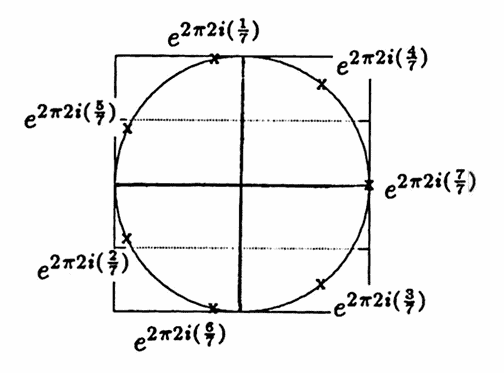 $$
\begin{gather}
k = 2\cr
N = 7
\end{gather}
$$
$$
\begin{gather}
k = 2\cr
N = 7
\end{gather}
$$
Let $\,N \gt 1\,$ be a positive integer, and let $\,k\,$ be a fixed integer between $\,1\,$ and $\,N - 1\,.$ Then:
$$ \begin{gather} \sum_{n=0}^{N-1} e^{2\pi ki(\frac nN)} = 0\cr \text{and}\cr \sum_{n=0}^{N-1} e^{-2\pi ki(\frac nN)} = 0 \end{gather} $$Proof of Proposition 2
Recall that, for all complex numbers $\,x\ne 1\,$:
$$ 1 + x + \cdots + x^{N-1} = \frac{1-x^N}{1-x} $$Let $\,x = e^{2\pi ki(\frac 1N)}\,$; since $\,k \lt N\,,$ $\,x\,$ is not equal to $\,1\,.$ Then,
$$ \begin{align} &\sum_{n=0}^{N-1} e^{2\pi ki(\frac nN)}\cr\cr &\quad = \sum_{n=0}^{N-1} x^n\cr\cr &\quad = \frac{1- x^N}{1-x}\cr\cr &\quad = \frac{1 - e^{2\pi ki(\frac NN)}}{1-x}\cr\cr &\quad = 0\ , \end{align} $$since $\,e^{2\pi ki} = 1\,$ for all integers $\,k\,.$ Letting $\,x = e^{-2\pi ki(\frac 1N)}\,$ and repeating the argument completes the proof. $\blacksquare$
Next, some questions concerning arbitrary sums of sinusoids are addressed.
In Question 3, Section 1.4, two periodic functions, each with fundamental period $\,4\,,$ were summed to yield a periodic function with fundamental period $\,2\,.$ Thus, the period of a sum certainly need not be the least common multiple of the summands. However, the following theorem, from [C&P, p. 35], shows that sinusoids are considerably nicer in this respect.
Let $\,P_1,P_2,\ldots,P_m\,$ be distinct positive integers, and let
$$ g(t) = \sum_{k=1}^m a_k\cos\frac{2\pi t}{P_k} + b_k\sin\frac{2\pi t}{P_k}\ , $$where $\,a_k\,$ and $\,b_k\,$ are real numbers, not simultaneously zero ($\,a_k^2 + b_k^2 \gt 0\,$).
Then, $\,g\,$ is periodic, and has fundamental period equal to the least common multiple of the integers $\,P_1,\ldots,P_m\,.$
Example: Actual Period versus Apparent Period
Consider the sum:
$$ g(t) = \sin 2\pi(\frac 15)t + \sin 2\pi(\frac{1}{5.1})t $$Using Lemma 3 in Section 1.4, scaling $\,g\,$ by $\,s = 10\,$ produces the scaled function:
$$ g_s(t) = \sin 2\pi(\frac 1{50})t +\sin 2\pi(\frac 1{51})t $$Using Theorem 2, the scaled function $\,g_s\,$ has fundamental period equal to the least common multiple of $\,50\,$ and $\,51\,,$ i.e., $\,50\cdot 51 = 2550\,.$
Then, using Lemma 3 in Section 1.4, $\,g\,$ has fundamental period $\,\frac{2550}{10} = 255\,.$
The first graph below shows that the function $\,g\,$ certainly ‘appears’ to have period $\,5\,.$ The remaining graphs illustrate that $\,g\,$ actually has period $\,255\,.$
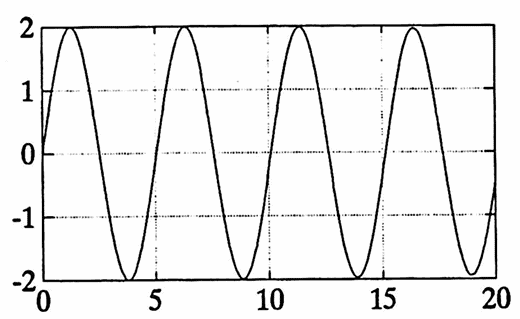
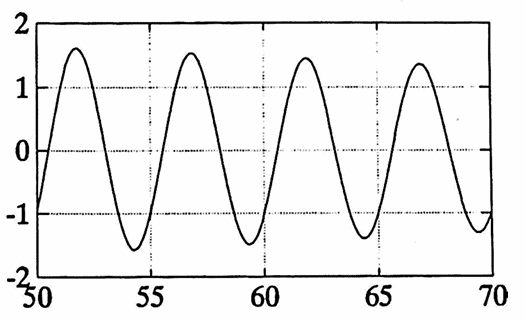
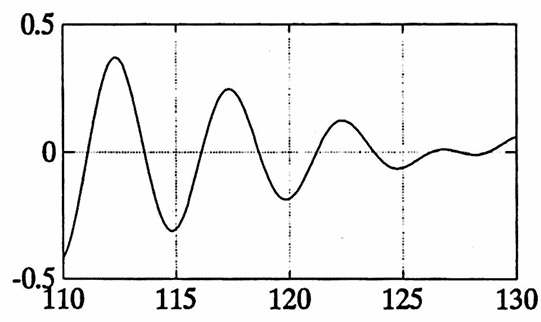
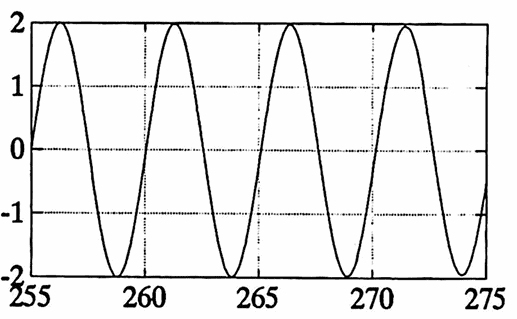
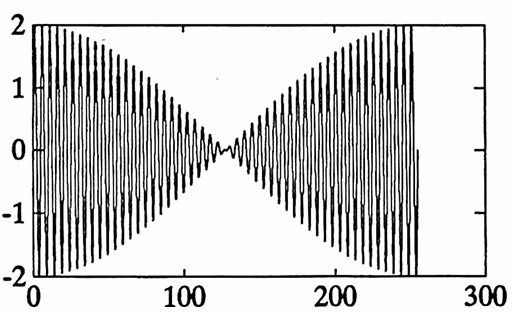
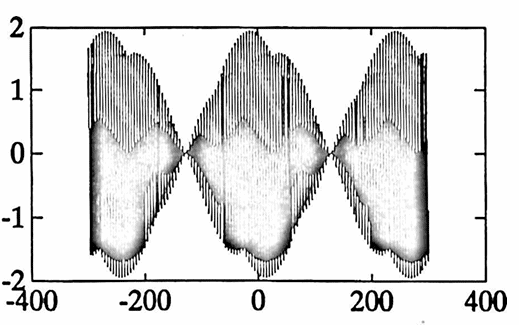
It is interesting to note that when two sinusoids with close amplitudes $\,A\,$ and $\,A + \Delta A\,,$ close fundamental periods $\,P\,$ and $\,P + \Delta P\,,$ and close phase shifts $\,\phi\,$ and $\,\phi + \Delta\phi\,$ are summed, then the resulting function ‘appears to be’ (at least initially) a sinusoid with period $\,P\,,$ amplitude $\,2A\,,$ and phase shift $\,\phi\,.$
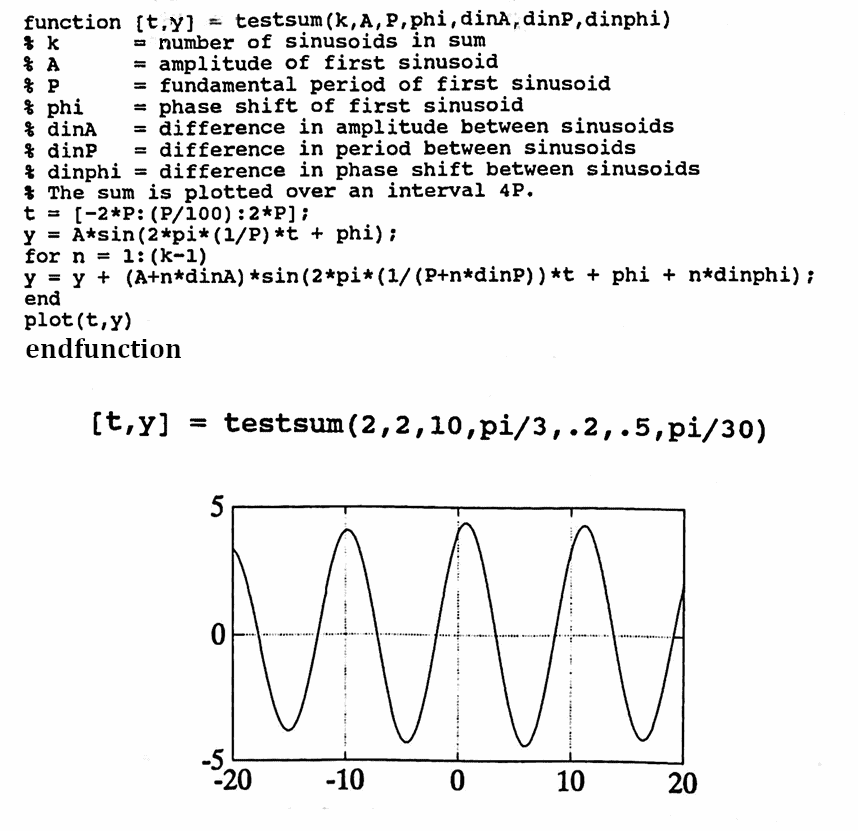
The following MATLAB function can be used to ‘play with’ this observation:
MATLAB Implementation: Sums of Sinusoids
Let $\,k\,$ be a positive integer, and let:
$$ \begin{gather} A\gt 0\,,\ \ P\gt 0\,,\ \ -\pi\le\phi\lt\pi\,,\cr\cr \Delta A\ge 0\,,\ \ \Delta P\ge 0\,,\ \ \Delta\phi\ge 0 \end{gather} $$The following MATLAB function takes the inputs $\,k\,,$ $\,A\,,$ $\,P\,,$ $\,\phi\,,$ $\,\Delta A\,,$ $\,\Delta P\,,$ $\,\Delta\phi\,,$ and plots a function $\,y\,,$ where:
$$ y = \sum_{n=0}^{k-1} (A + n\Delta A) \sin\left(2\pi\bigl(\frac 1{P + n\Delta P}\bigr)t + (\phi + n\Delta\phi)\right) $$An example of the use of this function is given.
The last topic to be considered in this section is that of equally-spaced sampling from sinusoids, which can give rise to a phenomena known as aliasing.
The English usage of the word ‘alias’ as a noun means an assumed name. Generalize this usage a bit to mean an assumed appearance. With this generalization, the name ‘aliasing’ to describe the following phenomenon should seem very appropriate.
Anyone who has watched Westerns on television and focused on the wagon wheels has observed that as these wheels turn faster and faster, they may actually appear to slow down, or even to stop or reverse direction, as the wagon’s speed increases. This assumed appearance (alias!) is due to equally-spaced sampling of the pictures in time, as described below.
Imagine a circular wheel with one spoke which is spinning at some uniform rate, say, once every $\,T\,$ seconds, in a dark room. If one was to flash a light precisely every $\,T\,$ seconds (or any multiple of $\,T\,$ seconds) then one would see the spoke in the same position each time, and perhaps perceive that the wheel was not spinning at all.
Now let $\,S\,$ be a little bit less than $\,T\,,$ and flash the light every $\,S\,$ seconds. The first time the light flashes, the spoke is seen in some position. Then, $\,S\,$ seconds later, the spoke has not quite reached that same position, so it appears to have backed up a little bit. Another $\,S\,$ seconds, and it appears to have backed up a bit more. Thus it appears to be moving backwards slowly (which is, of course, not the case at all!)
One more time. Now let $\,S\,$ be a little more than $\,T\,.$ The first time the light flashes, the spoke is seen in some position. Then, $\,S\,$ seconds later, the spoke has gone around once and a little bit more, so it appears to have moved forward slightly. Continue. The spoke appears to be moving forward at a rate that is much slower than the actual rate.
In the previous scenarios, it is said that one frequency has been ‘aliased’ into another frequency due to the process of taking equally spaced samples.
The same kind of aliasing can occur when one takes equally-spaced samples from sinusoids. Consider for example the sample data points below:
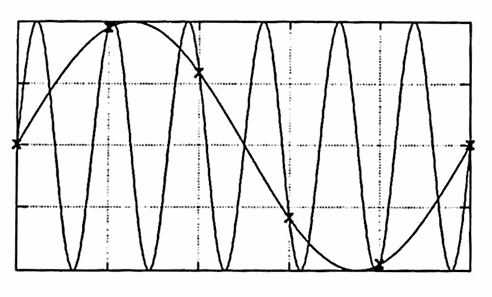
These sample points could have come from either of the sinusoids shown.
It is possible, in fact, to completely describe all the sinusoids that will pass through the same equally-spaced sample points.
Let
$$ A\sin(2\pi ft + \phi) $$be any sinusoid with amplitude $\,A\,$ and cyclic frequency $\,f\,.$
Suppose that data samples are taken at intervals of time $\,T\,$; that is, at times $\,kT\,,$ for all integers $\,k\,.$ Let $\,m\,$ denote any integer, so that $\,mk\,$ is also an integer. Then:
$$ \begin{align} &A\sin\bigl(2\pi f(kT) + \phi\bigr)\cr\cr &\quad = A\sin\bigl( 2\pi kTf + \phi\bigr)\cr\cr &\quad = A\sin\bigl(2\pi kTf + 2\pi mk + \phi\bigr)\cr\cr &\quad = A\sin\bigl(2\pi kT(f + \frac{mk}{kT}) + \phi\bigr)\cr\cr &\quad = A\sin\bigl(2\pi kT(f + \frac mT\bigr) + \phi\bigr) \end{align} $$Comparing the sinusoids
$$ A\sin\bigl(2\pi f(kT) + \phi\bigr) $$and
$$ A\sin\bigl(2\pi (f + \frac mT)(kT) + \phi\bigr) $$shows that the sinusoids $\,A\sin\bigl(2\pi f(kT) + \phi\bigr)\,$ and $\,A\sin\bigl(2\pi (f + \frac mT)(kT) + \phi\bigr)\,$ are indistinguishable for every integer $\,m\,$ with respect to samples taken at intervals of time $\,T\,.$
The final theorem of this section is the famous Sampling Theorem [S&H, 45–49], which relates sampling rates to truncated Fourier series:
Let $\,f\,$ be a sum of harmonically related sinusoids:
$$ f(t) = \frac{a_0}2 + \sum_{k=1}^K \left( a_k\cos\frac{2\pi kt}P + b_k\sin\frac{2\pi kt}P \right) $$To be able to recover $\,f\,$ exactly, it is necessary to sample at a rate greater than twice the highest harmonic number $\,K\,.$
That is, letting $\,N\,$ denote the number of (equally-spaced) samples in a fundamental period $\,P\,,$ one must have $\,N \gt 2K\,.$