1.4 More On Periodic Functions
Let $\,\Bbb P\,$ denote the set of all periods of a real-valued function $\,f\,$ defined on some subset of $\,\Bbb R\,.$
If $\,f\,$ has any nonzero period $\,p\,,$ then Lemma 2 of Section 1.3 shows that $\,\Bbb P\,$ contains all integer multiples of $\,p\,.$
Can there be anything else in $\,\Bbb P\,$? More generally, what can $\,\Bbb P\,$ (as a subset of $\,\Bbb R\,$) look like? This is the first question to be addressed in this section.
First, a preliminary definition:
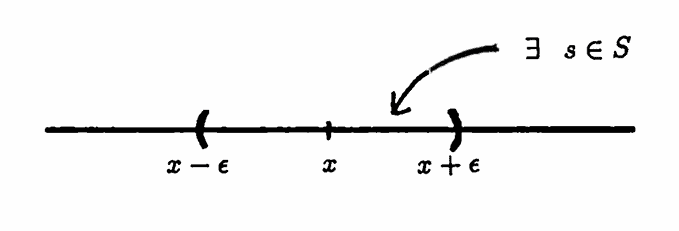
A set $\,S\,$ is dense in $\,\Bbb R\,$ if there are elements of $\,S\,$ arbitrarily close to any real number.
Precisely, $\,S\,$ is dense in $\,\Bbb R\,$ if and only if for every $\,x\in\Bbb R\,$ and for every $\,\epsilon \gt 0\,,$ there exists $\,s\in S\,$ with $\,|x-s| \lt \epsilon\,.$
The sketch below suggests a geometric view of this definition.
The next theorem completely characterizes what the set of all periods of a function can look like.
[adapted from Olm, p. 549]
Let $\,f\,$ be a real-valued function with $\,\cal D(f)\subset\Bbb R\,,$ and let $\,\Bbb P\,$ be the set of all periods of $\,f\,.$
The set $\,\Bbb P\,$ satisfies exactly one of the following properties:
(a) $\Bbb P = \{0\}\,$; in this case, $\,f\,$ is not periodic.
(b) $\Bbb P\,$ consists of all integral multiples of some least positive period $\,P\,,$ also called the fundamental period of $\,f\,.$
(c) $\Bbb P\,$ is dense in $\,\Bbb R\,$; in this case, $\,\cal D(f)\,$ is also dense in $\,\Bbb R\,,$ and there is no least positive period.
The next lemma is used in the proof of Theorem 1.
The set $\,\Bbb P\,$ of all periods of a function $\,f\,$ is closed under addition, subtraction, and multiplication by an arbitrary integer.
Proof of Lemma 1
Let $\,p_1\,$ and $\,p_2\,$ be in $\,\Bbb P\,,$ and let $\,x\in \cal D(f)\,.$ Then, $\,x + p_1\in \cal D(f)\,,$ so also $\,(x + p_1) + p_2 \in \cal D(f)\,.$ Furthermore:
$$ \begin{align} &f(x + (p_1 + p_2))\cr\cr &\quad = f((x+p_1) + p_2)\cr\cr &\quad = f(x+p_1)\cr &\qquad \text{($\,p_2\,$ is a period)}\cr\cr &\quad = f(x)\cr &\qquad \text{($\,p_1\,$ is a period)} \end{align} $$This implies that $\,p_1 + p_2\,$ is a period of $\,f\,,$ and thus $\,\Bbb P\,$ is closed under addition.
The fact that $\,\Bbb P\,$ is closed under multiplication by an arbitrary integer follows from Lemma 2 of Section 1.3. In particular, $\,-p_2\,$ is a period of $\,f\,,$ so that closure under addition implies that $\,p_1 + (-p_2) = p_1 - p_2\,$ is also a period of $\,f\,.$ Thus, $\,\Bbb P\,$ is also closed under subtraction. $\blacksquare$
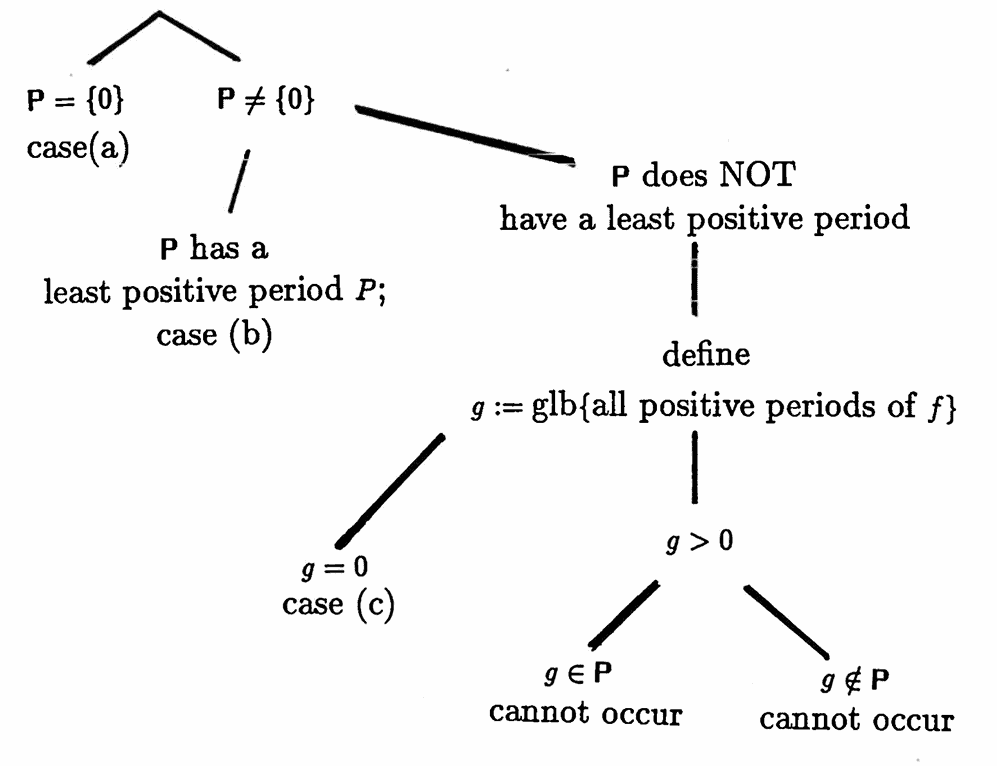
The logical structure of Theorem 1's proof is summarized in the flow chart below.
Proof of Theorem 1
The set $\,\Bbb P\,$ always contains $\,0\,,$ since $\,0\,$ is a period of every function. If $\,0\,$ is the only element in $\,\Bbb P\,,$ then $\,f\,$ has no nonzero period, and is not periodic. This is case (a).
If $\,\Bbb P \ne \{0\}\,,$ then there exists $\,p\ne 0\,$ in $\,\Bbb P\,.$ Since both $\,p\,$ and $\,-p\,$ are periods of $\,f\,,$ it can be assumed that $\,p\,$ is positive.
Either $\,\Bbb P\,$ has a least positive period, or not. If so, let $\,P\,$ denote the least positive period, and let
$$ B := \{nP\ |\ n\in\Bbb Z\}\,, $$so that $\,B\,$ consists of all integer multiples of $\,P\,.$ Since every integer multiple of $\,P\,$ is a period of $\,f\,,$ it is always true that $\,B\subset \Bbb P\,.$
Suppose for contradiction that $\,B\subsetneq \Bbb P\,,$ so that there exists $\,\tilde p\in\Bbb P\,$ with $\,\tilde p\notin B\,.$ Without loss of generality, suppose that $\tilde p\gt 0\,.$
Covering $\,\Bbb R\,$ by intervals of the form
$$(nP\,,\,(n+1)P]\,,\ n\in \Bbb Z\,,$$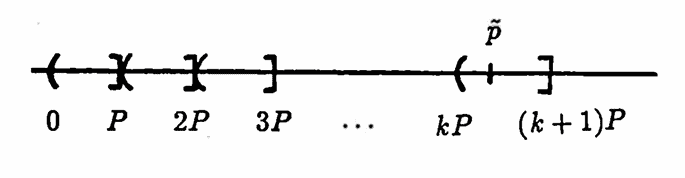
it must be that $\,\tilde p\in (kP\,,\,(k+1)P]\,$ for some positive integer $\,k\,.$ But then, $\,\tilde p - kP\in (0,P]\,,$ so that (via Lemma 1) $\,\tilde p - kP\,$ is a strictly positive period of $\,f\,$ that is less than $\,P\,$; a contradiction. Thus, $\,B = \Bbb P\,$; this is case (b).
It remains only to show that if $\,\Bbb P\,$ does not have a least positive period, then $\,\Bbb P\,$ is dense in $\Bbb R\,.$
Define $\,g\,$ to be the greatest lower bound of all positive periods in $\,\Bbb P\,.$ Either $\,g = 0\,,$ or $\,g \gt 0\,.$
If $\,g = 0\,,$ then there exist arbitrarily small positive periods. In particular, given any $\,\epsilon \gt 0\,,$ there exists a positive period $\,p_\epsilon\,$ with $\,p_\epsilon \lt \epsilon\,.$
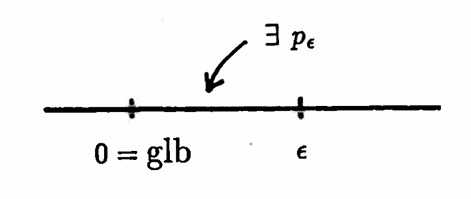
Then,
$$ \{kp_\epsilon\ |\ k\in\Bbb Z\} \subset \Bbb P\,, $$and:
$$ \{x+kp_\epsilon\ |\ x\in \cal D(f)\,,\ k\in\Bbb Z\} \subset \cal D(f) $$Let $\,y\,$ be any real number, and cover $\,\Bbb R\,$ by intervals of the form $\,(kp_\epsilon\,,\,(k+1)p_\epsilon]\,$ for $\,k\in\Bbb Z\,.$ Thus, there exists an integer $\,j\,$ with:
$$ y\in (jp_\epsilon\,,\,(j+1)p_\epsilon] $$Since the interval $\,(jp_\epsilon\,,\,(j+1)p_\epsilon]\,$ has length $\,p_\epsilon\,$ which is less than $\,\epsilon\,,$ the distance from $\,y\,$ to $\,(j + 1)p_\epsilon\,$ is less than $\,\epsilon\,.$ Hence, $\,(j + 1)p_\epsilon\,$ is an element of $\,\Bbb P\,$ within $\,\epsilon\,$ of $\,y\,,$ from which it is concluded that $\,\Bbb P\,$ is dense in $\,\Bbb R\,.$
To see that $\,\cal D(f)\,$ is dense in $\,\Bbb R\,,$ repeat the previous argument, this time covering $\,\Bbb R\,$ by intervals of the form
$$ (x+kp_\epsilon\,,\,x+(k+1)p_\epsilon]\,, $$where $\,x\,$ is a fixed element of $\,\cal D(f)\,.$
Thus, both $\,\Bbb P\,$ and $\,\cal D(f)\,$ are dense in $\,\Bbb R\,.$
It is shown next that $\,g \gt 0\,$ cannot occur. For if $\,g \gt 0\,,$ then either $\,g\in\Bbb P\,$ or $\,g\notin\Bbb P\,.$ If $\,g\in\Bbb P\,,$ then $\,g\,$ would be a least positive period; but the current assumption is that $\,\Bbb P\,$ has no least positive period.
Thus, it must be that $\,g\notin\Bbb P\,.$ Then, there exist positive periods arbitrarily close to $\,g\,.$ In particular, given $\,\epsilon\,$ with $\,0\lt\epsilon\lt g\,,$ there exist distinct positive periods $\,p_1\,$ and $\,p_2\,$ with $\,0\lt p_1-p_2\lt\epsilon\lt g\,.$
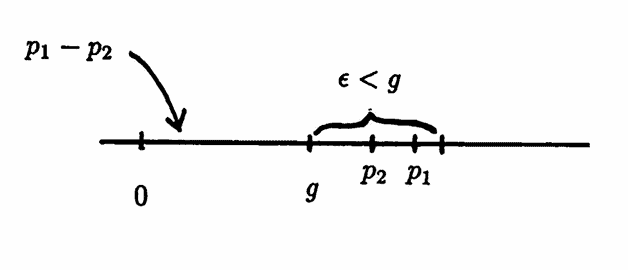
Via Lemma 1, $\,p_1-p_2\,$ is a period of $\,f\,,$ and $\,p_1-p_2\,$ is strictly less $\,g\,$; contradicting the fact that $\,g\,$ is the greatest lower bound. Case (c) has now been proven. $\blacksquare$
A useful consequence of Theorem 1 is:
Every discrete-domain periodic function has a least positive period.
Proof of Corollary 1
Let $\,f\,$ be a discrete-domain periodic function. By definition of a discrete-domain function, the elements of $\,\cal D(f)\,$ come from a time list.
No time list can be dense in $\,\Bbb R\,.$ To see that this is the case, let $\,t_1\,$ and $\,t_2\,$ be two consecutive entries in the time list, so that $\,t_1\lt t_2\,.$ Define $\,\epsilon := t_2 - t_1\,,$ so that $\,\epsilon\gt 0\,.$ Then, the midpoint $\,t :=\frac{t_1+t_2}{2}\,$ is an element of $\,\Bbb R\,$ with no time list entry within, say, $\,\frac\epsilon 3\,$ of $\,t\,.$
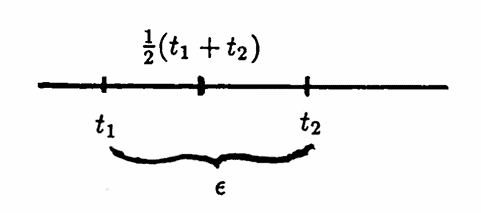
Thus, the domain of a discrete-domain function cannot be dense in $\,\Bbb R\,,$ which excludes case (c) of Theorem 1. Since $\,f\,$ is periodic, case (a) does not hold. Thus, case (b) holds, and $\,f\,$ has a least positive period. $\blacksquare$
It is important to note that the domain of a discrete-domain periodic function need not be a uniform time list, as the example below illustrates.
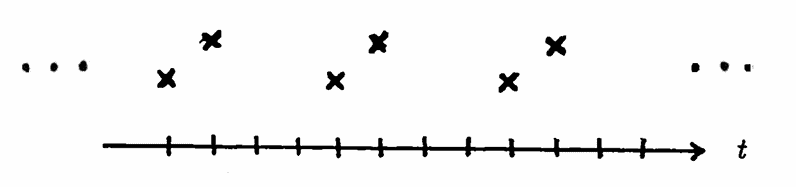
Least Positive Period $\,= 4$
To avoid topological digressions, any discussion of continuity of periodic functions is restricted to periodic functions with domain $\,\Bbb R\,$ (having its usual topology).
The next theorem characterizes periodic functions defined on $\,\Bbb R\,$ that have no least positive period.
Let $\,f:\Bbb R\rightarrow\Bbb R\,$ be a periodic function with no least positive period. Then $\,f\,$ is either constant, or everywhere discontinuous.
Proof of Theorem 2
By Theorem 1, the set $\,\Bbb P\,$ of all periods of $\,f\,$ is dense in $\,\Bbb R\,.$ To show that $\,f\,$ is either constant or everywhere discontinuous, it is shown, equivalently, that if f is not everywhere discontinuous, then it is constant.
So suppose that $\,f\,$ is continuous at $\,x = a\,,$ and suppose for contradiction that $\,f\,$ is not constant. Then, there exists $\,b\,$ with $\,f(b)\ne f(a)\,.$
Choose $\,\epsilon\,$ with $\,0\lt\epsilon\lt |f(b)-f(a)|\,.$ By continuity of $\,f\,$ at $\,a\,,$ there exists $\,\delta\gt 0\,$ such that whenever $\,|x - a|\lt\delta\,,$ one has $\,|f(x) - f(a)|\lt\epsilon\,.$
Consequently, whenever $\,x\,$ is within the $\delta$-interval about $\,a\,,$ $\,f(x)\ne f(b)\,.$ However, since the periods of $\,f\,$ are dense in $\,\Bbb R\,,$ there exists a period $\,p\,$ with $\,0\lt p\lt\delta\,.$ On the interval $\,[a, a + p] \subset [a, a + \delta)\,,$ $\,f\,$ must take on all the values in its range, in particular, $\,f(b)\,.$
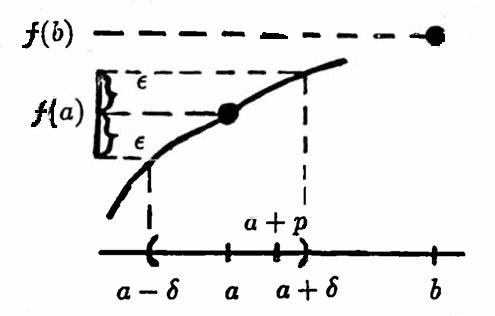
This yields the desired contradiction. $\blacksquare$
A summary
To summarize: by Corollary 1, every discrete-domain periodic function has a least positive period and, by Theorem 2, if a periodic function defined on $\,\Bbb R\,$ has no least positive period, then it is either ‘uninteresting’ (constant), or ‘very unusual’ (everywhere discontinuous).
To avoid the problems associated with periodic functions having no least positive period, in the remainder of this text, it is assumed that all periodic functions have a least positive (fundamental) period.
The remainder of this section investigates sums of periodic functions, where each summand has a fundamental period. The next definition provides a method of comparing real numbers that is very important in this context.
Two nonzero real numbers $\,p\,$ and $\,q\,$ are commensurable if and only if the ratio $\,\frac pq\,$ is a rational number.
A finite set of nonzero real numbers $\,\{p_1,p_2,\ldots,p_n\}\,$ is commensurable if and only if the ratios $\,\frac{p_i}{p_j}\,$ are rational numbers, for all $\,i,j\in \{1,2,\ldots,n\}\,.$
Examples
Every pair of nonzero rational numbers is commensurable, as is every finite set of nonzero rational numbers.
The numbers $\,\sqrt 2\,$ and $\,3\sqrt{2}\,$ are commensurable.
The numbers $\,2\,$ and $\,\pi\,$ are not commensurable. Indeed, any finite set that contains at least one rational number and at least one irrational number is not commensurable.
The questions addressed next arise naturally when investigating sums of periodic functions.
Question 1
Question: Must a sum of periodic functions be periodic?
Answer: No. The classic counterexample is provided by the sum:
$$\sin x + \sin\pi x$$Here, $\,\sin x\,$ and $\,\sin \pi x\,$ have fundamental periods $\,2\pi\,$ and $\,2\,,$ respectively, but the sum is not periodic. (The proof is a simple consequence of Theorem 5 or Theorem 6 in [O&T].) Note that the fundamental periods of the summands are not commensurable in this case.
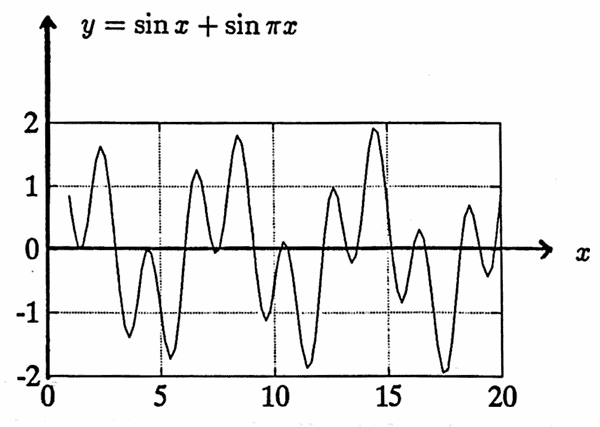
It will be shown in Theorem 3 that a sum of functions with commensurable least positive periods must be periodic. However, the next example shows that, even in this case, the sum need not have a least positive period.
Question 2
Question: If a sum of functions with least positive periods is periodic, must the sum have a least positive period?
Answer: [C&P, p. 33] No. The functions $\,f\,$ and $\,g\,$ defined below each have fundamental period $\,1\,.$ Their sum $\,f + g\,$ is periodic, but (as shown in Section 1.3) has no least positive period.
$$ f(x) = \cases{ 1 & \text{ for } x\in\Bbb Z\cr 0 & \text{ for } x\notin \Bbb Z } $$ $$ g(x) = \cases{ 1 & \text{ for } x\in\Bbb Q \text{ and } x\notin\Bbb Z\cr 0 & \text{ for } x\notin\Bbb Q \text{ or } x\in\Bbb Z } $$ $$ (f+g)(x) = \cases{ 1 & \text{ for } x\in\Bbb Q\cr 0 & \text{ for } x\notin \Bbb Q } $$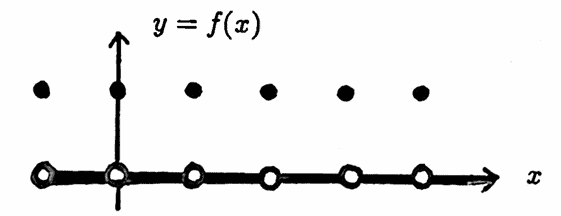
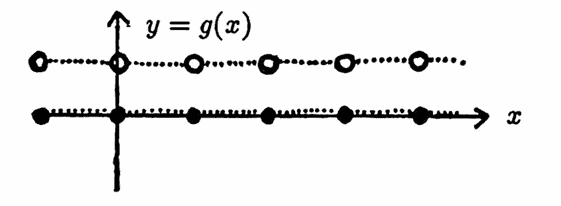
Question 3
Question: Suppose that two functions have the same least positive period, and their sum has a least positive period. Must the sum have the same least positive period as the summands?
Answer: No. Consider functions $\,f\,$ and $\,g\,$ with common domain $\,\Bbb Z\,,$ and with output lists given below. Both $\,f\,$ and $\,g\,$ have fundamental period $\,4\,,$ but their sum has fundamental period $\,2\,.$ For an example using continuous summands, see [C&P, p. 32].

This last example can be further generalized. Indeed, the fundamental period of the sum can be made as small as desired, without changing the fundamental period of the summands, as illustrated by the output lists given below. For an example using continuous summands, see [C&P, p. 33].
Theorem 3 addresses the question: What are the possible candidates for the fundamental period of a sum?
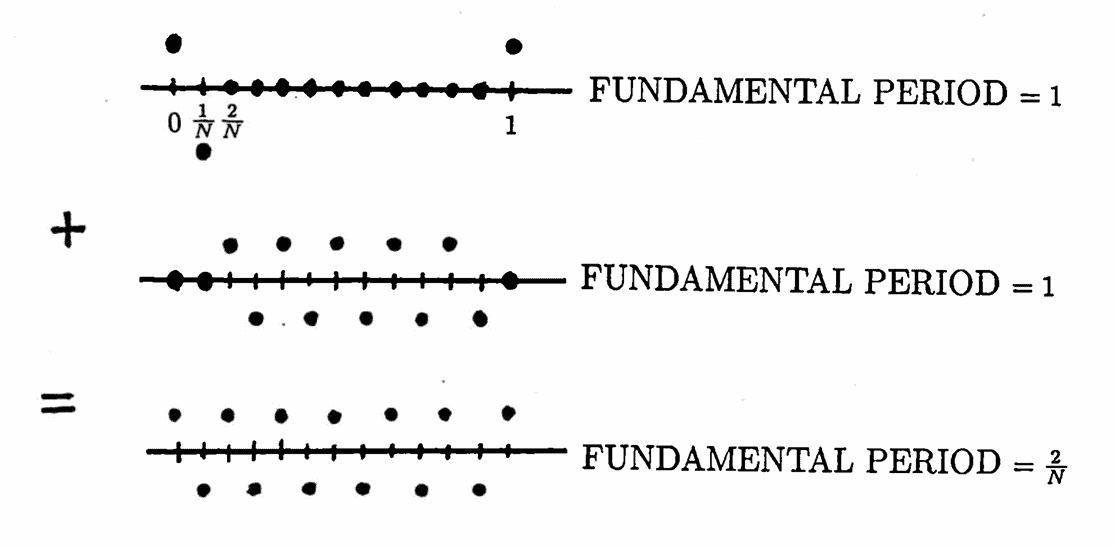
The next theorem assures that a sum of periodic functions with commensurable least positive periods is itself periodic:
If functions $\,f_1,f_2,\ldots,f_N\,$ have a common domain $\,\cal D\,$ and commensurable least positive periods $\,P_1,P_2,\ldots,P_N\,,$ then the sum $\,f_1+\cdots+f_N\,$ is periodic.
The proof of Theorem 3 makes use of the next three lemmas.
If $\,p\,$ and $\,q\,$ are commensurable, then there exist integers $\,n\,$ and $\,d\,$ ($\,d\ne 0\,$) with $\,p = (\frac nd)q\,.$
Proof of Lemma 2
By definition of commensurable numbers, the ratio $\,\frac pq\,$ is rational. Thus, there exist integers $\,n\,$ and $\,d\,$ with $\,\frac pq = \frac nd\,,$ from which $\,p = (\frac nd)q\,.$ $\blacksquare$
Let $\,s\,$ be a fixed positive real number.
A function $\,f\,$ has fundamental period $\,P\,$ if and only if the function $\,g\,$ defined by
$$ g(xs) := f(x)\ \ \text{for all}\ x\in \cal D(f) $$has fundamental period $\,sP\,.$
The function $\,g\,$ in this lemma is referred to as ‘the function $\,f\,,$ with domain scaled by $\,s\,$’.
A periodic function $\,f\,$ and ‘scaled’ functions $\,g\,$ are shown below, for two different choices of the scaling factor $\,s\,.$
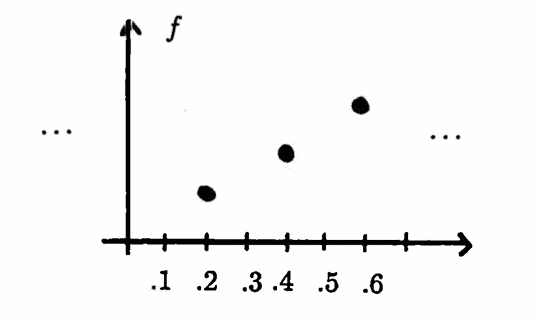
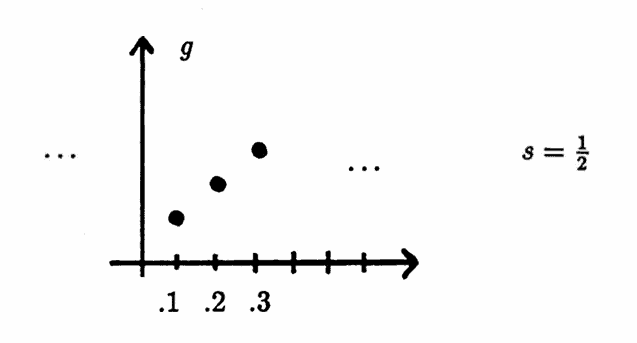
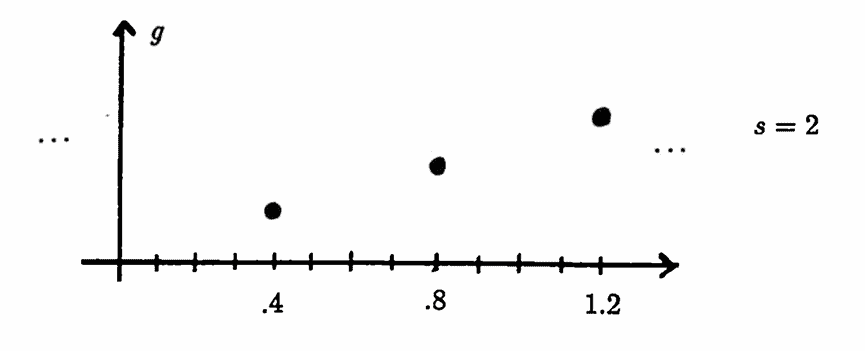
Proof of Lemma 3
[adapted from C&P, p. 35]
“$\implies$” Let $\,f\,$ have least positive period $\,P\,.$ For a given positive real number $\,s\,,$ the domain of $\,g\,$ is:
$$ {\cal D(g)} = \{y\in\Bbb R\ |\ y=xs\ \text{ for some }\ x\in\cal D(f)\} $$Whenever $\,x\in\cal D(f)\,,$ so are $\,x\pm P\,,$ which implies that $\,(x\pm P)s = xs\pm sP\,$ are in the domain of $\,g\,.$ Let $\,y\in\cal D(g)\,,$ and write $\,y = xs\,$ for some $\,x\in \cal D(f)\,.$ Then:
$$ \begin{align} g(xs \pm sP) &= g \bigl((x \pm P)s\bigr)\cr &\qquad \text{(regroup)}\cr\cr &:= f(x \pm P)\cr &\qquad \text{(definition of $\,g$)}\cr\cr &= f(x)\cr &\qquad \text{($f\,$ has period $\,P$)}\cr\cr &:= g(xs)\cr &\qquad \text{(definition of $\,g$)} \end{align} $$This shows that $\,g\,$ has period $\,sP\,.$
A preliminary observation is necessary before showing that $\,sP\,$ is the least positive period of $\,g\,.$ Observe that $\,\cal D(f)\,$ can be written as:
$$ {\cal D(f)} = \{\frac ys\ |\ y\in \cal D(g)\}\tag{*} $$To see this, let $\,x\in \cal D(f)\,$; then $\,\, xs\in \cal D(g)\,,$ and so $\,\frac{xs}s\in \{\frac ys\ |\ y\in\cal D(g)\}\,.$ That is, $\,x\in \{\frac ys\ |\ y\in \cal D(g)\}\,.$
Also, if $\,x\in\{\frac ys\ |\ y\in \cal D(g)\}\,,$ then $\,x = \frac{\hat xs}{s} = \hat x\,$ for some $\,\hat x\in\cal D(f)\,,$ so that $\,x\in \cal D(f)\,.$
Now it is shown that $\,sP\,$ is the least positive period of $\,g\,.$ If $\,P_1\,$ is any positive number less than $\,sP\,,$ write $\,P_1 = s\tilde P\,,$ where $\,\tilde P \lt P\,.$ If $\,g\,$ has period $\,s\tilde P\,,$ then it must be that, for every $\,x\in\cal D(f)\,$:
$$ g(xs\pm s\tilde P) = g(xs)\tag{**} $$Since $\,xs\pm s\tilde P\in\cal D(g)\,,$ (*) shows that $\,x\pm \tilde P\in \cal D(f)\,.$ But since $\,g(xs + s\tilde P) = f(x\pm \tilde P)\,$ and $\,g(xs) = f(x)\,,$ (**) implies that $\,f(x \pm \tilde P) = f(x)\,$ for every $\,x\in \cal D(f)\,,$ so that $\,\tilde P\,$ is a period of $\,f\,$ that is strictly less than $\,P\,.$ This contradicts the fact that $\,P\,$ is the least positive period of $\,f\,.$ Therefore, $\,sP\,$ must be the least positive period of $\,g\,.$
“$\impliedby\,$” For the remaining argument, use the result just proven to scale the function $\,g\,$ by $\,\frac 1s\,,$ to obtain $\,f\,.$ $\blacksquare$
Let $\,f_1,\ldots,f_N\,$ be functions with a common domain $\,\cal D\,,$ and let $\,s \gt 0\,.$
Scale each $\,f_i\,$ by $\,s\,$ to obtain a corresponding scaled function $\,g_i\,,$ as per Lemma 3. Then:
$$ \begin{gather} \text{$p\,$ is a (fundamental) period of $\,f := \sum_{i=1}^N f_i$}\cr \iff\cr \text{$sp\,$ is a (fundamental) period of $\,g := \sum_{i=1}^N g_i$} \end{gather} $$Proof of Lemma 4
Since the functions $\,f_i\,$ have a common domain $\,\cal D\,,$ the functions $\,g_i\,$ have a common domain
$$ {\cal D}_s := \{xs\ |\ x\in \cal D \}\ ,$$which is also the domain of the sum $\,g\,.$ Also, for every $\,x\in\cal D\,$:
$$ \begin{align} g(xs) &:= \sum_{i=1}^N g_i(xs)\cr\cr &:= \sum_{i=1}^N f_i(x)\cr\cr &:= f(x) \end{align} $$‘$\implies$’ If $\,p\,$ is any period of $\,f\,,$ and $\,xs\,$ is any element in $\,\cal D_s\,,$ then
$$ \begin{align} g(xs\pm sp) &= g\bigl( (x\pm p)s\bigr)\cr &= f(x\pm p)\cr &= f(x)\cr &= g(xs)\,, \end{align} $$so that $\,sp\,$ is a period of $\,g\,.$
‘$\impliedby$’ If $\,sp\,$ is a period of $\,g\,,$ then, for every $\,x\in\cal D\,,$
$$ f(x\pm p) = g\bigl((x\pm p)s\bigr) = g(xs) = f(x)\,, $$so that $\,f\,$ has period $\,p\,.$
An argument similar to that in Lemma 3 shows that the current lemma holds true with ‘period’ replaced by ‘fundamental period’. $\blacksquare$
Now, the proof of Theorem 3:
Proof of Theorem 3
[adapted from C&P, p. 34] Suppose that functions $\,f_1,\ldots,f_N\,$ have a common domain $\,\cal D\,$ and commensurable least positive periods $\,P_1,\ldots,P_N\,.$
Then, the pairs $\,\{P_1,P_i\}\,$ for $\,2\le i\le N\,$ are commensurable, so that by Lemma 2 there exist integers $\,n_i\,$ and $\,d_i\,$ ($\,2 \le i\le N\,$) with:
$$ P_i = \bigl(\frac{n_i}{d_i}\bigr)P_1\tag{*} $$Let $\,M\,$ be any common multiple of the integers $\,d_2,\ldots,d_N\,,$ and define $\,s := \frac{M}{P_1}\,.$ Since $\,f_i\,$ has least positive period $\,P_i\,,$ using Lemma 3 and scaling by $\,s\,$ produces a counterpart scaled function $\,g_i\,$ with least positive period
$$ \begin{align} sP_i &:= \bigl(\frac{M}{P_1}\bigr)P_i\cr\cr &= \bigl(\frac{Mn_i}{d_iP_i}\bigr)P_i\ \ \ \text{(using (*))}\cr\cr &= \frac{Mn_i}{d_i}\cr\cr &\in\Bbb Z\,,\ \text{for all}\ i = 2,\ldots,N\,, \end{align} $$where membership in $\,\Bbb Z\,$ results from $\,M\,$ being a common multiple of the $\,d_i\,.$ Also, $\,sP_1 = M\in\Bbb Z\,.$ So, the functions $\,f_i\,$ have ‘scaled’ counterparts $\,g_i\,$ which have integer least positive periods $\,sP_i\,,$ for $\,i = 1,\ldots,N\,.$
The integer
$$ (sP_1)(sP_2)\cdot\,\ldots\,\cdot(sP_N)\tag{**} $$is a period of each $\,g_i\,,$ and hence a period of the sum $\,g\,.$ By Lemma 4, any rearrangement of (**) in the form $\,s\cdot K\,$ shows that $\,K\,$ is a period of $\,f\,.$ Thus, $\,f\,$ is periodic. $\blacksquare$
Although Theorem 3 guarantees that the sum of periodic functions with commensurable least positive periods is itself periodic, it cannot guarantee that the sum has a fundamental period (see the answer to Question 2). Fortunately, the situation with discrete-domain periodic functions is considerably nicer:
Every finite sum of discrete-domain periodic functions with a common domain is a discrete-domain periodic function with a least positive period.
Proof of Corollary 2
Let $\,f_1,\ldots,f_N\,$ be discrete-domain periodic functions with a common domain $\,\cal D\,.$ By Corollary 1, each function $\,f_i\,$ has a least positive period $\,P_i\,,$ for $\,i=1,\ldots,N\,.$ It is argued next that these least positive periods must be commensurable.
Suppose for contradiction that there exists a ratio $\,\frac PQ\,$ that is irrational, where $\,P = P_i\,$ and $\,Q = P_j\,$ for some $\,i\,$ and $\,j\,$ between $\,1\,$ and $\,N\,,$ $\,i\ne j\,.$
Choose any $\,x\in\cal D\,.$ Since $\,\cal D\,$ is a common domain and $\,P\,$ is a period of a summand, $\,x\pm kP\in\cal D\,$ for every $\,k\in\Bbb Z\,.$ Then, since $\,Q\,$ is a period of a summand, it must be that $\,(x\pm kP)\pm jQ\in\cal D\,,$ for every $\,k,j\in\Bbb Z\,.$ In particular, $\,x + (kP + jQ)\in\cal D\,$ for all integers $\,k\,$ and $\,j\,.$
However, the set $\,\{kP+jQ\ |\ k\in\Bbb Z\,,\ j\in\Bbb Z\}\,$ is dense in $\,\Bbb R\,$ since $\,P\,$ and $\,Q\,$ are incommensurable positive numbers [Olm, Theorem 4]. Thus, $\,\cal D\,$ must be dense in $\,\Bbb R\,.$ However, the domain of a discrete-domain function cannot be dense in $\,\Bbb R\,$: this supplies the necessary contradiction. Thus, the least positive periods of the summands must be commensurable.
Theorem 3 shows that the sum is a periodic discrete-domain function, which must have a least positive period by Corollary 1. $\blacksquare$
Question 4
Question: Suppose that functions $\,f_1,f_2,\ldots,f_N\,,$ each defined on $\,\Bbb R\,,$ have fundamental integer periods $\,P_1,P_2,\ldots,P_N\,,$ respectively. In this case, the fundamental periods are commensurable, so the sum is periodic. If the sum has a fundamental period, what are the candidates for this fundamental period?
Caveny and Page have answered this question in [C&P, pp. 38–41], and their result is presented next. In what follows, the notation ‘$\,lcm\,$’ means least common multiple, and $\,a|b\,$ means that $\,a\,$ divides $\,b\,,$ i.e., $\,b/a\,$ is an integer. Furthermore, two integers are relatively prime if and only if they have no common factors other than $\,1\,.$
[C&P, pp. 38–41] Let $\,P_1,P_2,\ldots,P_N\,$ be positive integers.
If there exist real-valued functions $\,f_1,f_2,\ldots,f_N\,$ defined on $\,\Bbb R\,$ with respective fundamental periods $\,P_1,P_2,\ldots,P_N\,,$ such that the sum $\,f := f_1 + \cdots + f_N\,$ has fundamental period $\,P\,,$ then the number $\,P\,$ must satisfy the following conditions:
(a) $\,P = \frac uv\,,$ where $\,u\,$ and $\,v\,$ are relatively prime integers, and $\,u\,$ satisfies the following two conditions:
(b) $\,u\ |\ lcm(P_1,P_2,\ldots,P_N)\,$; and
(c) $\,u\,$ is divisible by each prime power that divides precisely one $\,P_i\,$ ($\,1 \le i \le N\,$).
Conversely, whenever a real number $\,P\,$ satisfies (a), (b), and (c), then there exist real-valued functions $\,f_1,\ldots,f_N\,$ defined on $\,\Bbb R\,$ with respective fundamental periods $\,P_1,\ldots,P_N\,,$ such that the sum $\,f_1 + \cdots + f_N\,$ has fundamental period $\,P\,.$
The following examples illustrate the use of this theorem.
The first example shows how the result can be used with summands that have commensurable (but not integer) fundamental periods. The second example shows how the result can be used to obtain some information about sums of discrete-domain periodic functions.
Example: Using Theorem 4 with Non-Integer Periods
[C&P, p. 40] Suppose that functions $\,g_1\,,\, g_2\,,\, g_3\,$ and $\,g_4\,$ are defined on $\,\Bbb R\,$ and have respective fundamental periods $\,Q_1 = 3\alpha\,,$ $\,Q_2 = \frac{13}4\alpha\,,$ $\,Q_3 = \frac 72\alpha\,,$ and $\,Q_4 = \frac{15}4\alpha\,,$ where $\,\alpha\,$ is irrational.
Scaling each function by $\,s := \frac 4\alpha\,$ yields functions $\,f_i\,$ ($\,1\le i\le 4\,$) with respective integer fundamental periods $\,P_1 := Q_1s = 12\,,$ $\,P_2 := Q_2s = 13\,,$ $\,P_3 := Q_3s = 14\,$ and $\,P_4 := Q_4s = 15\,.$ (A general procedure for producing such a scaling factor is discussed following the example.)
The prime factorizations of the $\,P_i\,$ are:
$$ \begin{align} P_1 &= 2^2\cdot 3\cr P_2 &= 13\cr P_3 &= 2\cdot 7\cr P_4 &= 3\cdot 5 \end{align} $$Observe that:
$$ lcm(P_1,P_2,P_3,P_4) = 2^2\cdot 3\cdot 5\cdot 7\cdot 13 $$What are the prime powers that divide precisely one $\,P_i\,$?
- $2^2\,$ only divides $\,P_1$
- $13\,$ only divides $\,P_2$
- $7\,$ only divides $\,P_3$
- $5\,$ only divides $\,P_4$
If the sum $\,f := f_1 + f_2 + f_3 + f_4\,$ has a least positive period $\,P\,,$ then $\,P\,$ must be of the form $\,P = \frac uv\,,$ where $\,u\,$ and $\,v\,$ are relatively prime, $\,u\,$ divides $\,2^2\cdot 3\cdot 5\cdot 7\cdot 13\,,$ and $\,u\,$ is divisible by $\,2^2\,,$ $\,13\,,$ $\,7\,$ and $\,5\,.$
Thus, either $\,u = 2^2\cdot 13\cdot 7\cdot 5 = 1820\,$ or $\, u = 3\cdot (2^2\cdot 13\cdot 7\cdot 5) = 5460\,.$ So the candidates for $\,P\,$ are:
$$ \begin{gather} \left\{\frac{1820}v\ |\ \substack{\text{$v\,$ is a positive integer}\\ \text{relatively prime to $1820\,$}}\right\} \cr \text{or}\cr \left\{\frac{5460}v\ |\ \substack{\text{$v\,$ is a positive integer}\\ \text{relatively prime to $5460\,$}}\right\} \end{gather} $$Scaling back to the original functions $\,g_i\,$ by using the scale factor $\,\frac 1s = \frac\alpha 4\,,$ the candidates for the fundamental period of $\,g_1 + g_2 + g_3 + g_4\,$ are:
$$ \begin{gather} \left\{\frac{1820}v\cdot\frac\alpha 4\ |\ \substack{\text{$v\,$ is a positive integer}\\ \text{relatively prime to $1820\,$}}\right\} \cr \text{or}\cr \left\{\frac{5460}v\cdot\frac\alpha 4\ |\ \substack{\text{$v\,$ is a positive integer}\\ \text{relatively prime to $5460\,$}}\right\} \end{gather} $$Any more specific information about the fundamental period of the sum $\,g_1 + g_2 + g_3 + g_4\,$ would require additional information about the functions $\,g_i\,.$
As illustrated in the preceding example, the requirement in Theorem 4 that the fundamental periods $\,P_1,\ldots,P_N\,$ be integers is easily overcome by applying a common scaling factor.
Indeed, whenever functions $\,f_1,\ldots,f_N\,$ have commensurable fundamental periods, then a common scaling factor $\,s\,$ can always be applied (if necessary) to obtain a new, scaled, set of functions that have integer periods. To do this, suppose that the respective fundamental periods of the $\,f_i\,$ are
$$ r_1\alpha\,,\ \ldots\,,\,r_N\alpha\ ,\tag{*} $$where the $\,r_i\,$ are rational and $\,\alpha\,$ is a (possible) irrational factor. Rewrite the rational factors $\,r_i\,$ as equivalent fractions with least common denominator $\,D\,,$ so that the list in (*) becomes:
$$ \frac{a_1\alpha}D\,,\,\ldots\,,\,\frac{a_N\alpha}D $$The $\,a_i\,$ are integers. Scaling by $\,\frac D\alpha\,$ then produces a new set of functions with respective fundamental integer periods $\,a_1,\ldots,a_N\,.$
Before using Theorem 4 with discrete-domain functions, it is necessary to understand how the set of periods of a discrete-domain function compares to the set of periods of its extension to $\,\Bbb R\,.$ This is the content of Lemma 5.
Suppose that $\,f\,$ is a discrete-domain periodic function, with domain $\,\cal D\,.$ Let $\,f_e\,$ denote the extension of $\,f\,$ to $\,\Bbb R\,$ defined by:
$$ f_e(x) = \cases{ f(x) & \text{for }\ x\in\cal D\cr 0 & \text{for }\ x\notin\cal D } $$Let $\,\Bbb P\,$ denote the set of periods of $\,f\,,$ and let $\,\Bbb P_e\,$ denote the set of periods of $\,f_e\,.$ Then, $\,\Bbb P \subset \Bbb P_e\,.$ It is possible for the containment to be proper.
Proof of Lemma 5
Let $\,f\,,$ $\,f_e\,,$ $\,\cal D\,,$ $\,\Bbb P\,$ and $\,\Bbb P_e\,$ be as in the statement of the lemma. To show that $\,\Bbb P\subset \Bbb P_e\,,$ suppose that $\,P\,$ is a period of $\,f\,,$ and let $\,x\in\Bbb R\,.$ Either $\,x\in\cal D\,$ or $\,x\notin\cal D\,.$
If $\,x\in\cal D\,,$ then so is $\,x \pm P\,,$ and:
$$ \begin{align} f_e(x\pm P) &= f(x\pm P)\cr &\qquad\text{(definition of $\,f_e\,$)}\cr\cr &= f(x)\cr &\qquad\text{($\,P\,$ is a period of $\,f\,$)}\cr\cr &= f_e(x)\cr &\qquad\text{(definition of $\,f_e\,$)} \end{align} $$If $\,x\notin\cal D\,,$ then neither are $\,x\pm P\,,$ so both $\,f_e(x) = 0\,$ and $\,f_e(x\pm P) = 0\,.$ Thus, $\,P\,$ is a period of $\,f_e\,,$ so $\,P \in\Bbb P_e\,.$
The examples below illustrate that $\,\Bbb P_e\,$ can be strictly larger than $\,\Bbb P\,.$ $\blacksquare$
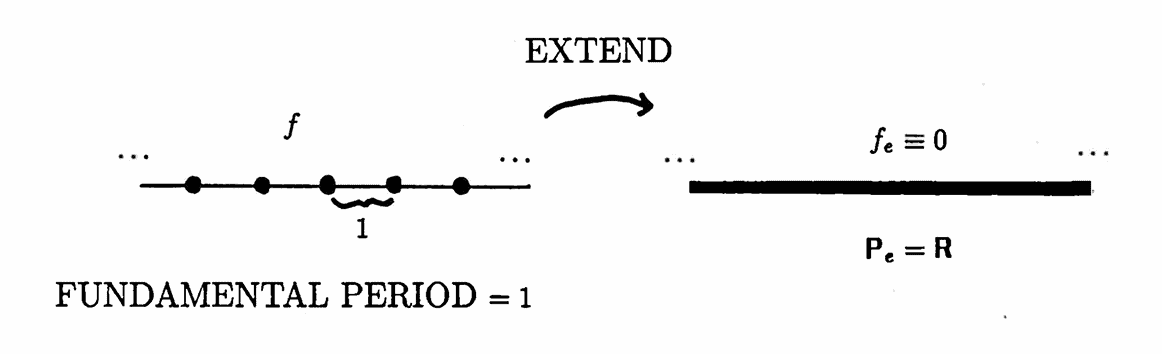
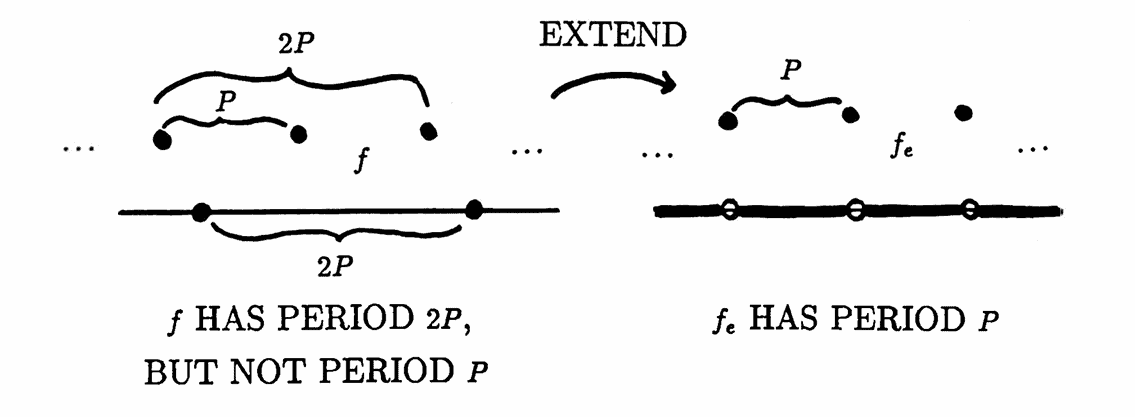
It is a consequence of Lemma 5 that if $\,P\notin \Bbb P_e\,,$ then $\,P\notin \Bbb P\,.$ This observation is used in the next example.
Example: Using Theorem 4 with Discrete-Domain Functions
(It will be instructive for the reader to compare the discussion here with the answer to Question 3.)
Suppose that discrete-domain periodic functions $\,f\,$ and $\,g\,$ both have fundamental period $\,4\,,$ and a common domain. Suppose further that $\,f\,$ and $\,g\,$ are such that their extensions $\,f_e\,$ and $\,g_e\,$ to $\,\Bbb R\,$ still have fundamental period $\,4\,.$
Now, apply Theorem 4 to $\,(f+g)_e = f_e + g_e\,.$ The candidates for the period of this (extended) sum are of the form $\,\frac uv\,,$ where $\,u\,$ and $\,v\,$ are relatively prime and $\,u|4\,.$ (In this case, there is no prime power that divides precisely one $\,P_i\,.$) Thus, $\,u\,$ must equal $\,1\,,$ $\,2\,,$ or $\,4\,,$ so the candidates for the period of $\,f_e + g_e\,$ are:
$$ \begin{gather} \bigl\{ \frac 1v\ |\ \substack{\text{$\,v\,$ is a positive integer}\cr \text{greater than $\,1\,$}} \bigr\}\cr \text{or}\cr \bigl\{ \frac 2v\ |\ \substack{\text{$\,v\,$ is any positive integer}\cr \text{relatively prime to $\,2\,$}} \bigr\}\cr \text{or}\cr \bigl\{ \frac 4v\ |\ \substack{\text{$\,v\,$ is any positive integer}\cr \text{relatively prime to $\,4\,$}} \bigr\} \end{gather} $$If $\,P\,$ is not one of the numbers in these sets, then $\,P\,$ cannot be a period of $\,f+g\,.$