1.3 Periodicity

In this section, some basic properties of periodic functions are carefully established, from a viewpoint that favors investigation of periodicities in discrete-domain data.

The next section addresses more delicate properties of periodic functions.

Introduction to Periodic Functions

Roughly, a periodic function is one with values that repeat some basic pattern. The graphs of two periodic functions are shown below.

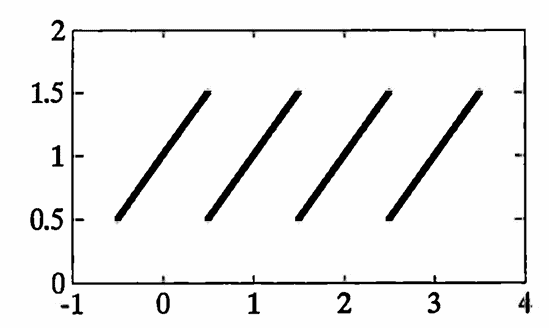
The usual definition of a periodic function is adapted, as follows, to better suit the investigation of periodicities in discrete-domain data:

The symbol  ‘$\,\pm\,$’  is read as ‘plus or minus’, and the abbreviation  ‘$\,x \pm p\,$’  is used for  ‘$\,x + p\ \ \text{ or }\ \ x-p\,$’ .

Similarly,  ‘$\,f(x \pm p)\,$’  is shorthand for:

The requirement that both $\,x + p\,$ and $\,x - p\,$ be in the domain of $\,f\,$ is essential. It assures that one can always move both to the right and to the left in the domain of $\,f\,.$ Without this requirement, it is possible to have ‘functions with a nonzero period’ that no reasonable person would want to call periodic, as illustrated in a later example.

Here are some immediate consequences of the definition just given:

Every function has period $\,0\,,$ since $\,f(x \pm 0) = f(x)\,$ for all $x \in {\cal D}(f)\,.$

Whenever a function $\,f\,$ has a period $\,p\,,$ it also has a period $\,-p\,.$ This is a consequence of the symmetry in the definition. Thus, if a function $\,f\,$ has any nonzero period, then it necessarily has a positive period.

A constant function $\,f : \Bbb R \to \Bbb R\,$ has all periods, since for all real numbers $\,x\,$ and $\,p\,,$ $\,f(x \pm p) = f(x)\,.$

Example:  A Function with Rational Number Periods

Define $\,g : \Bbb R \to \Bbb R\,$ by:

Every rational number is a period of this function, and these are the only periods. To see this, argue as follows:

Let $\,p\,$ be any rational number. Then,

and

which shows that every rational number is a period of $\,g\,$. The argument used the fact that a sum of rational numbers is rational; and the sum of a rational and irrational number is irrational.

To see that no irrational number is a period, let $\,p\,$ be any irrational number, and choose $\,x := -p\,.$ Thus, $\,x\,$ is irrational, so $\,g(x) = 0\,.$

However, $\,x + p = -p + p = 0\,$ is rational, so $\,g(x + p) = 1\,.$ Thus, $\,g(x) = g(x + p)\,$ does not hold for all $\,x\,,$ so the irrational number $\,p\,$ is not a period of $\,g\,.$

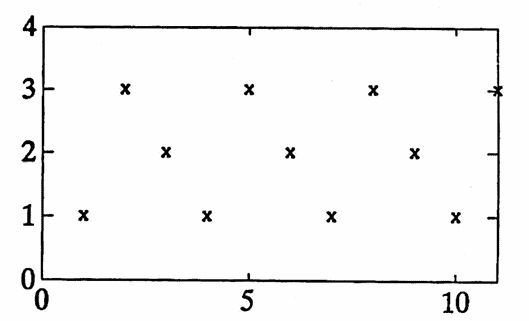
Example:  A Function with Period $\,2$

The discrete-domain function $\,f\,$ graphed below has period $\,2\,.$ Observe that it also has periods $\,2k\,$ for all integers $\,k\,.$

The next result gives a way to build ‘new’ periodic functions from functions with a common domain and a common period.

Proof

Recall that the functions $\,f\pm g\,,$ $\,fg\,,$ $\,kf\,$ and $\,\frac fg\,$ are defined by:

Now, for every $\,x\in \cal D\,$:

This shows that $\,f + g\,$ also has a period $\,p\,.$ The remaining cases are similar.   $\blacksquare$

By induction, it follows easily that Lemma 1 also holds for all finite sums and products.

For example, suppose that functions $\,f\,,$ $\,g\,$ and $\,h\,$ have common domain $\,\cal D\,$ and a common period $\,p\,.$ Then, one application of the lemma shows that $\,f+g\,$ has a period $\,p\,$; a second application shows that $\,(f + g) + h\,$ has a period $\,p\,.$

If a pattern repeats itself on an interval of length $\,p\,,$ then it necessarily repeats itself on intervals of length $\,2p\,,$ $\,3p\,,$ $\,4p,\,\ldots\,.$ This idea is formalized next.

Proof:  A Typical Induction Argument

The proof proceeds by induction. Let $\,S(k)\,$ be the statement:

‘ $\,f\,$ has a period $\,kp\,$’

The function $\,f\,$ has period $\,0\cdot p = 0\,,$ since $\,f(x \pm 0) = f(x)\,$ for all $\,x \in \cal D(f)\,.$ Thus, $\,S(0)\,$ is true.

In what follows, it is shown that whenever $\,S(k)\,$ is true (for $\,k \ge 0\,$), then $\,S(k + 1)\,$ is also true. Since $\,-p\,$ is a period of $\,f\,$ whenever $\,p\,$ is, this will complete the proof.

For induction, suppose that $\,f\,$ has period $\,kp\,$ (i.e., $\,S(k)\,$ is true). Then:

In particular, both $\,x + (k+1)p\,$ and $\,x - (k+1)p\,$ are in $\,\cal D(f)\,.$ Furthermore:

It has been shown that whenever $\,x\in \cal D(f)\,,$ so are $\,x \pm (k+1)p\,,$ and $\,f(x) = f\bigl( x \pm (k+1)p\bigr)\,.$ Thus, $\,f\,$ has a period $\,(k + 1)p\,.$ Therefore, $\,S(k + 1)\,$ is true.   $\blacksquare$

Proof

Suppose that $\,f\,$ has a period $\,p\,.$ Let $\,x\,$ and $\,y\,$ be in the domain of $\,f\,,$ with $\,|x - y| = |p|\,.$ Switching names, if necessary, suppose that $\,x \ge y\,.$

If $\,p \ge 0\,,$ then $\,x = y + p\,,$ and so:

If $\,p \lt 0\,,$ then $\,y = x + p\,,$ and so:

In either case, $\,f(x) = f(y)\,.$

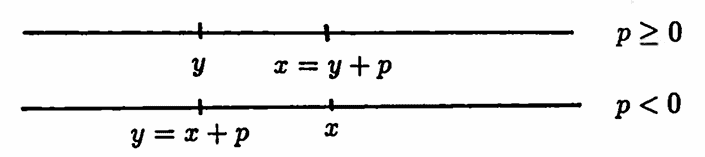
By the previous lemma, $\,f\,$ also has periods $\,kp\,,$ for all $\,k \in \Bbb Z\,.$ So if $\,|x - y| = |kp|\,,$ then an application of the result just proved shows that $\,f(x) = f(y)\,.\ \ \blacksquare$

The next lemma shows that if a function has a positive period $\,p\,,$ then on any half-open interval of length $\,p\,,$ the function must take on all of its function values. Thus, there is no ‘natural starting place’ for the repeating pattern that the function exhibits.

The sketch below illustrates that a function with a positive period $\,p\,$ may not take on all its function values on an open interval of length $\,p\,.$ It is interesting to note that this is a ‘fault’ of the definition of the length of an interval; the intervals $\,(a, b)\,,$ $\,[a, b]\,,$ $\,[a, b)\,$ and $\,(a, b]\,$ all have the same length.

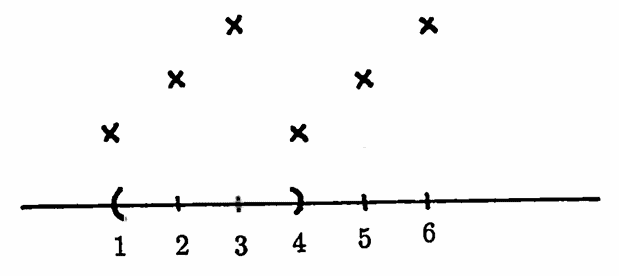
Period $\,3\,$; take $\,I := (1,4)$

Proof

Let $\,f\,$ have a positive period $\,p\,,$ and let $\,I\,$ be any half-open interval of length $\,p\,.$ Thus, $\,I\,$ is of the form $\,(a, b]\,$ or $\,[a, b)\,,$ where $\,b - a = p\,.$

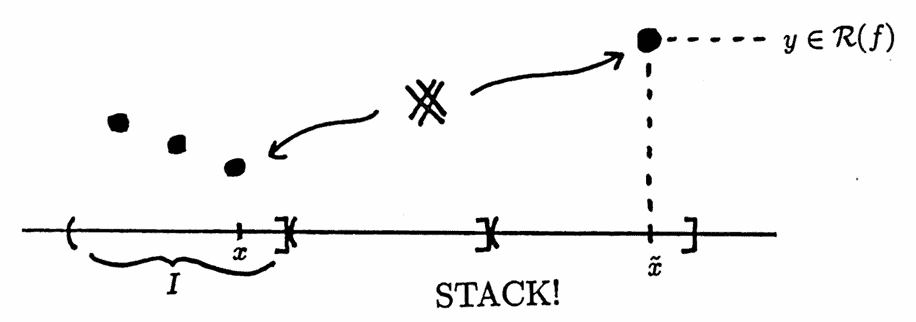
Suppose, for contradiction, that there is an output of $\,f\,$ which is not assumed in $\,I\,$;  that is, suppose there exists $\,y \in \cal R(f)\,$ for which there is no $\,x \in ({\cal D}(f) \cap I)\,$ with $\,f(x) = y\,.$

Since $\,y\in {\cal R}(f)\,,$ there must exist $\,\tilde x\in {\cal D}(f)\,$ with $\,y = f(\tilde x)\,.$ Write $\,\tilde x = x + np\,$ for some $\,x \in I\,,\ n \in \Bbb Z\,.$ (To see that this is always possible, merely place enough intervals of length $\,I\,$ end-to-end so that they eventually cover $\,\tilde x\,$. See the sketch below.)

Since $\,\tilde x\,$ is in the domain of $\,f\,,$ and the distance from $\,\tilde x\,$ to $\,x\,$ is a multiple of $\,p\,,$ $\,x\,$ is also in $\,{\cal D}(f)\,.$ Furthermore,

yielding the desired contradiction.   $\blacksquare$

It is tempting to simplify the definition of a periodic function as follows:

Proposed Definition:  The function $\,f\,$ has a period $\,p\,$ if the domain of $\,f\,$ contains $\,x + p\,$ whenever it contains $\,x\,,$ and if

for all $\,x\in {\cal D}(f)\,.$

With this ‘proposed definition’, a function need not have a period $\,-p\,$ whenever it has a period $\,p\,.$

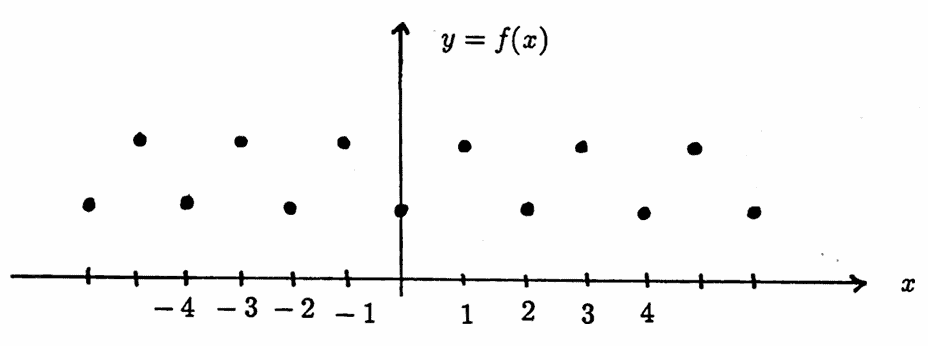
For example, the function graphed below has a period $\,2\,,$ but not a period $\,-2\,.$

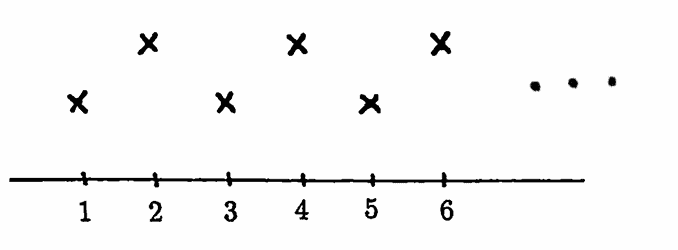
Domain = $\,\{1,2,3,\ldots\}$

The problem with this ‘proposed definition’ is that it is possible to define functions with nonzero periods that no reasonable person would want to call periodic. This is illustrated in the next example.

Example

Define a function $\,f\,$ as follows:  let $\,0\in {\cal D}(f)\,,$ and require $\,f\,$ to have periods $\,1\,$ and $\,\pi\,$ (as per the ‘proposed definition’).

Then, the numbers $\,1,2,3,4,\ldots\,$ must all be in $\,{\cal D}(f)\,,$ as must $\,\pi,2\pi,3\pi,4\pi,\ldots\,.$

Then, all elements of the form $\,k + n\pi\,$ must be in $\,{\cal D}(f)\,,$ where $\,k\,$ and $\,n\,$ are nonnegative integers. Now, the set $\{k + n\pi\ |\ k\ge 0,\ n\ge 0\}$ is closed under addition, and forms $\,\cal D(f)\,.$

Define $\,f\,$ to be $\,1\,$ everywhere on its domain. A moment’s reflection confirms that $\,f\,$ does indeed have periods $\,1\,$ and $\,\pi\,.$

The problem, however, is this:  the graph of the function does not periodically repeat itself as one moves from left to right, since new domain elements are constantly being added!

In particular, the graph of $\,f\,$ does not repeat itself on intervals of length $\,1\,$ or $\,\pi\,,$ so most people would feel uncomfortable calling $\,f\,$ ‘periodic’. A partial graph of $\,f\,$ is shown next.

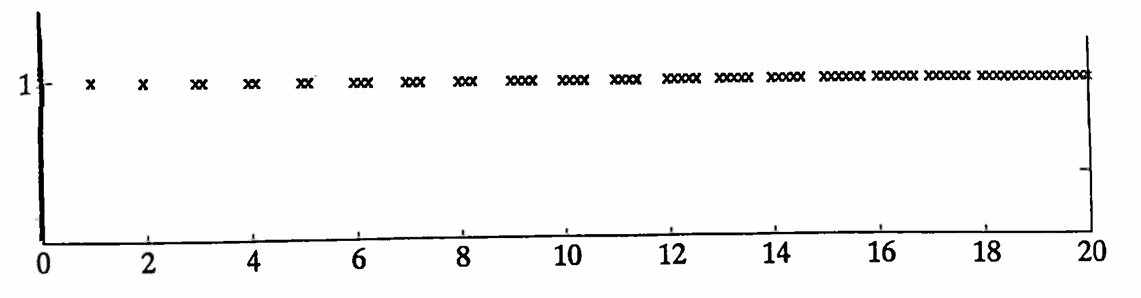
A ‘periodic’ function?

Thus far, this section has carefully established basic properties of functions with a period $\,p\,.$ Many interesting questions arise when one considers the set of all periods of a function.

Does every periodic function have a least positive period? (No.) If a periodic function does not have a least positive period, can anything be said about it? (Yes. The periods must be dense in $\Bbb R\,,$ and the function must be either constant, or everywhere discontinuous.)

Is the sum of two periodic functions (with different periods) necessarily periodic? (No.) If two functions have the same least positive period, must their sum have this same least positive period? (No.)

These are some of the questions addressed in Section 1.4.

Some Basic Reshaping Techniques

This section closes with some interesting ‘reshaping’ results that can be used, in certain cases, to identify periodic components in a finite list of real numbers. The next few definitions and notation will considerably simplify the statement and proof of the ‘reshaping’ theorem.

Thus, the mean of a sum of lists is the sum of the means of the component lists.

Proof of Lemma 5

First, it is shown that the result holds when $\,\boldsymbol{\rm S}\,$ is generated by only two lists. Thus, suppose that:

Then:

The remainder of the proof follows by induction. Suppose that the result holds for $\,K\,$ lists, where $\,K \ge 2\,$ is a fixed integer, and suppose that $\,S\,$ is a sum of $\,K + 1\,$ lists, denoted by $\,\boldsymbol{\rm x}_1,\ldots, \boldsymbol{\rm x}_{K+1}\,.$ Write

so that $\,S\,$ is viewed as a sum of two lists. Then,

where the inductive hypothesis was used in the second step.   $\blacksquare$

Observe that the mean of $\boldsymbol{\rm x} = (x_1,\ldots,x_p)\,$ is equal to the mean of any $p$-cycle $\,{}^r\boldsymbol{\rm x}\,,$ since:

and

Example

Suppose that a list $\,\boldsymbol{\rm S}\,$ of length $\,6\,$ is a sum of a $2$-cycle and a $3$-cycle, say:

There are of course an infinite number of ‘similar’ cycles that could have summed to yield $\,\boldsymbol{\rm S}\,,$ since given any constant $\,K\,$:

That is, one component can be shifted any given amount $\,K\,,$ provided that the remaining component is shifted the opposite amount, $\,-K\,.$ Thus, given only the sum list $\,\boldsymbol{\rm S} = (5,5,1,8,2,4)\,,$ it is impossible to recover the precise cycles that originally generated $\,\boldsymbol{\rm S}\,.$

However, it is possible in this case to recover zero-mean $\,2\,$ and $3$-cycles which, when added to $\,\mu_{\boldsymbol{\rm S}}\,,$ yield $\,\boldsymbol{\rm S}\,.$ Only some basic reshaping techniques are needed. The technique is presented in the proof of the next theorem.

Proof: Producing the Lists $\,\tilde{\boldsymbol{\rm x}}_0\,$ and $\,\tilde{\boldsymbol{\rm y}}_0$

The proof illustrates the procedure that yields the zero-mean lists $\,\tilde{\boldsymbol{\rm x}}_0\,$ and $\,\tilde{\boldsymbol{\rm y}}_0\,.$

Renaming, if necessary, suppose that $\,p \gt q\,.$ In the following summation of the two components forming $\,\boldsymbol{\rm S}\,,$ the notation $\,\boldsymbol{\rm y}_?\,$ is used to indicate that the exact subscript on $\,\boldsymbol{\rm y}\,$ depends on the relationship between $\,p\,$ and $\,q\,$:

Subtract $\mu_{\boldsymbol{\rm S}}\,$ from each entry in $\,\boldsymbol{\rm S}\,,$ and call the resulting list $\,\boldsymbol{\rm S}_0\,$ (since $\,\boldsymbol{\rm S}_0\,$ has mean $\,0\,$). To find $\,\boldsymbol{\rm x}_0\,,$ first reshape $\,\boldsymbol{\rm S}_0\,$ in rows of length $\,p\,$:

to get:

There are $\,\frac Np\,$ rows in the arrangement above. Summing the entries in each of the $\,p\,$ columns gives the column sums:

There are $\,\frac Nq\,$ sets of $\,(y_1,\ldots,y_q)\,$ in the entire list, and these are equally divided among the $\,p\,$ columns, since $\,p\,$ and $\,q\,$ are relatively prime. Thus, each column contains $\,\frac N{pq}\,$ sets of $\,(y_1,\ldots,y_q)\,,$ and hence:

Dividing each column sum by $\,\frac Np\,$ gives the averages of each column:

Since $\,\mu_{\boldsymbol{\rm S}} = \mu_{\boldsymbol{\rm x}} + \mu_{\boldsymbol{\rm y}}\,,$ these column averages can be written more simply as:

Therefore, the column averages of the reshaped list recover the list $\,\boldsymbol{\rm x}\,,$ with each entry decreased by $\,\mu_{\boldsymbol{\rm x}}\,.$ Define $\,\tilde{\boldsymbol{\rm x}}_0\,$ to be the list consisting of these column averages:

Clearly, $\,\tilde{\boldsymbol{\rm x}}_0\,$ has zero mean.

A similar reshaping of $\,\boldsymbol{\rm S}_0\,$ into $\,\frac Nq\,$ rows of $\,q\,$ each yields the column averages:

Then,

from which:

The theorem does not hold if $\,p\,$ and $\,q\,$ are not relatively prime, even if $\,N\,$ is a multiple of $\,pq\,.$ Also, the theorem does not hold if $\,p\,$ and $\,q\,$ are relatively prime, but $\,N\,$ is not a multiple of $\,pq\,.$

The constructive technique just discussed also works if $\,\boldsymbol{\rm S}\,$ is a sum of any finite number of relatively prime cycles, providing that $\,N\,$ is a multiple of the product of the cycles.

To see this, suppose that the theorem holds for $\,K\,$ cycles, and suppose that

where $\,\boldsymbol{\rm C}_i\,$ is a $p_i$-cycle.

The list $\,\boldsymbol{\rm C}\,$ is a $p_1p_2\cdots p_K$-cycle, which is relatively prime to $\,p_{K+1}\,,$ by hypothesis. Thus, applying the theorem to $\,\boldsymbol{\rm C}\,$ and $\,\boldsymbol{\rm C}_{K+1}\,$ yields:

Then, using the inductive hypothesis on $\,\tilde{\boldsymbol{\rm C}}\,,$ and the fact that $\,\mu_{\tilde{\boldsymbol{\rm C}}} = 0\,,$ one obtains:

In general, a positive integer $\,N\,$ may be viewed as a product of relatively prime integers in more than one way. For example, $\,30 = 2 \cdot 15 = 3 \cdot 10 = 5 \cdot 6\,.$ Thus, given a list $\,S\,$ of length $\,30\,,$ one might separately investigate the hypotheses that:

• $\boldsymbol{\rm S}\,$ is a sum of a $2$-cycle and a $15$-cycle;
• $\boldsymbol{\rm S}\,$ is a sum of a $3$-cycle and a $10$-cycle;
• $\boldsymbol{\rm S}\,$ is a sum of a $5$-cycle and a $6$-cycle.

Under what conditions will $\,N\,$ have a unique decomposition as a product of relatively prime integers? The next proposition answers this question.

Proof

“$\impliedby$”

Suppose that the prime decomposition of $\,N\,$ is of the form $\,N = p^mq^n\,$ for primes $\,p\ne q\,,$ $\,m\,$ and $\,n\,$ positive integers.

Then, $\,p^m\,$ and $\,q^n\,$ are relatively prime integers with product $\,N\,.$ Any other regrouping of the prime factors as a product of two numbers is necessarily of the form $\,N = d_1d_2\,,$ where either $\,d_1\,$ and $\,d_2\,$ have a common factor $\,p\,$; or $\,d_1\,$ and $\,d_2\,$ have a common factor $\,q\,.$

“$\implies$”

Suppose that $\,N\,$ has a unique representation as a product of relatively prime integers.

If $\,N\,$ has exactly one distinct prime in its prime decomposition, say $\,N = p^m\,$ for a prime $\,p\,$ and positive integer $\,m\,,$ then $\,N\,$ cannot be written as a product of relatively prime integers.

If $\,N\,$ has three or more primes in its prime decomposition, say N = $\,p^mq^nr^jx\,$ where $\,p\,,$ $\,q\,$ and $\,r\,$ are distinct primes, $\,m\,,$ $\,n\,$ and $\,j\,$ are positive integers, and $\,x\,$ is either $\,1\,$, or a product of primes other than $\,p\,,$ $\,q\,,$ and $\,r\,,$ then $\,N\,$ can be written as a product of two relatively prime integers in more than one way: say,

Thus, $\,N\,$ must have precisely two distinct primes in its prime factorization.   $\blacksquare$

Matlab Example

The following diary of an actual MATLAB session illustrates the reshaping procedure, while reviewing the necessary MATLAB commands.

The illustrated procedure could be implemented much more efficiently. However, efficient implementations often obscure simple underlying ideas. Therefore, in what follows, efficiency has been sacrificed for the sake of clarity.

% construct a 'known unknown':
%   a 2-cycle, 3-cycle and 5-cycle
x = [1 2];
x = [x x x x x x x x x x x x x x x];
% x is a 2-cycle of length 30
y = [-1 0 4];
y = [y y y y y y y y y y];
% y is a 3-cycle of length 30
z = [-1 3 1 2 0];
z = [z z z z z z];
% z is a 5-cycle of length 30
% sum the components to get the 'known unknown'
S = x + y + z;
% subtract off the mean of S to get SO
SO = S - mean(S);
% reshape SO to test for a 2-cycle,
%   using the 'reshape' command
r1 = reshape(S0,2,15)'

r1 =

   -4.5000   1.5000
    2.5000  -0.5000
   -2.5000   1.5000
   -0.5000  -0.5000
    3.5000  -2.5000
   -3.5000   5.5000
   -2.5000   0.5000
    1.5000  -3.5000
    0.5000   3.5000
   -1.5000  -1.5000
    0.5000   0.5000
   -1.5000   4.5000
   -3.5000  -2.5000
    4.5000  -1.5000
   -0.5000   2.5000

% average the columns, using the 'sum' command,
%   dividing by # of rows
r1 = sum(r1) / 15

r1 =
   -0.5000 0.5000

% Observe that this is precisely x - mean(x)!
temp = x - mean(x);
temp(1:2)

ans =
   -0.5000 0.5000

% Now, repeat, testing for the 3-cycle and 5-cycle
r2 = reshape(SO,3,10)';
r2 = sum(r2) / 10

r2 =
  -2   -1    3

r3 = reshape(SO,5,6)';
r3 = sum(r3) / 6

r3 =
  -2    2    0    1    -1

% Now, build r1, r2, and r3 into length-30 cycles
r1 = [r1 r1 r1 r1 r1 r1 r1 r1 r1 r1 r1 r1 r1 r1 r1];
r2 = [r2 r2 r2 r2 r2 r2 r2 r2 r2 r2];
r3 = [r3 r3 r3 r3 r3 r3];

% Sum r1, r2 and r3, and add  mean(S)  back in,
%   to recover S:

predict = r1 + r2 + r3 + mean(S)

predict =
  Columns 1 through 12
    -1  5  6  3  1  5  3  3  7  1  0  9
  Columns 13 through 24
     1  4  5  0  4  7  2  2  4  4  2  8
  Columns 25 through 30
     0  1  8  2  3  6

% Compare with S:
S - predict

ans =
  Columns 1 through 12
     0  0  0  0  0  0  0  0  0  0  0  0
  Columns 13 through 24
     0  0  0  0  0  0  0  0  0  0  0  0
  Columns 25 through 30
     0  0  0  0  0  0