 One-Step Conversions
One-Step Conversions
You have seen multiplying by $\,1\,$ in an appropriate form used to get a common denominator when adding fractions; this is only one of a multitude of uses for this important technique.
One of the most common applications of multiplying by $\,1\,$ in an appropriate form occurs in the context of unit conversion, which is the subject of this section and the next.
Often, in life, you're required to convert a quantity from one unit to another. For example, you might need to convert centimeters to inches; miles to feet; tablespoons to teaspoons; or feet/second (read as ‘feet per second’) to miles/hour (‘miles per hour’).
In such cases, you have a quantity of interest, but are seeking a new name for that quantity. The process of finding this new name is called unit conversion.
Important Fact
For example, since $\,1 \text{ meter} = 1000 \text{ millimeters}\,,$
$$ \cssId{s24}{\frac{1\text{ meter}}{1000\text{ millimeters}}} \cssId{s25}{= \frac{1000\text{ millimeters}}{1\text{ meter}}} \cssId{s26}{= 1} $$Or, since since $\,1 \text{ tablespoon} = 3 \text{ teaspoons}\,,$
$$ \cssId{s28}{\frac{1\text{ tablespoon}}{3\text{ teaspoons}}} \cssId{s29}{= \frac{3\text{ teaspoons}}{1\text{ tablespoon}}} \cssId{s30}{= 1} $$A ‘one-step’ conversion requires multiplying by the number $\,1\,$ only once.
Any unit of length can be converted to any other unit of length. For example,
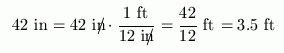
Or,
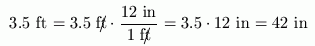
Notice the different names for the number $\,1\,$ needed in each case! In the first example, inches was on top, so we also needed inches on the bottom to cancel out. In the second example, feet was on top, so we also needed feet on the bottom to cancel out. Units cancel the same way that numbers cancel!
Any unit of time can be converted to any other unit of time. For example,
$$ \cssId{s47}{5\text{ sec}} \cssId{s48}{= 5{\text{ sec}\kern{-15px}/}\,\,\,\, \cdot \frac{1\text{ min}}{60\text{ sec}\kern{-15px}/}} \cssId{s49}{= \frac{5}{60}\text{ min}} \cssId{s50}{\approx 0.083\text{ min}} $$Any unit of volume can be converted to any other unit of volume, and so on.
Feel free to use scrap paper and a calculator to compute your answers. Use only the conversion information given in the Unit Conversion Tables to compute your answers.
Examples
If you get an exact answer that uses $\,3\,$ or fewer decimal places, then input the exact answer.
If your calculator answer is more than $\,3\,$ decimal places, then round your answer to $\,3\,$ decimal places. As usual, do not insert any commas in numbers. That is, input ‘$5280$’, not ‘$5{,}280$’.