 End Behavior of Polynomials
End Behavior of Polynomials
End Behavior of General Functions
Roughly, the ‘end behavior’ of a function refers to what happens to its graph as you travel ...
- ... farther and farther to the right; this is called right-hand end behavior
- ... farther and farther to the left; this is called left-hand end behavior
‘Farther and farther to the right’ means you let $\,x\,$ go to infinity, which is written as ‘$\,x\rightarrow\infty\,$’.
‘Farther and farther to the left’ means you let $\,x\,$ go to negative infinity, which is written as ‘$\,x\rightarrow-\infty\,$’.
End behavior is studied to understand what happens to the outputs from a function (the $y$-values of points on the graph) as you move farther and farther away from the origin.
For example, you might want to know:
- Are the outputs getting bigger and bigger, without bound?
- Are the outputs getting closer to zero?
- Are the outputs approaching some nonzero number?
In general, functions can have a variety of end behaviors, as shown in the table below. Only right-hand end behaviors are shown here.
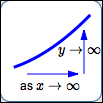
as $x\rightarrow\infty\,,$ $\,y\rightarrow\infty$
Read as:
‘as $\,x\,$ goes to infinity, $\,y\,$ goes to infinity’
|
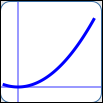 as in $\,y = x^2\,$
as in $\,y = x^2\,$
|

|
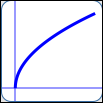 as in $\,y = \sqrt{x}\,$
as in $\,y = \sqrt{x}\,$
|

|
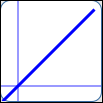 as in $\,y = x\,$
as in $\,y = x\,$
|
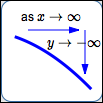
as $x\rightarrow\infty\,,$ $\,y\rightarrow-\infty$
Read as:
‘as $\,x\,$ goes to infinity, $\,y\,$ goes to negative infinity’
|
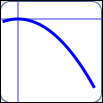 as in $\,y = -x^2\,$
as in $\,y = -x^2\,$
|
|
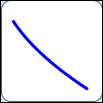
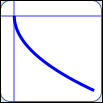 as in $\,y = -\sqrt{x}\,$
as in $\,y = -\sqrt{x}\,$
|

|
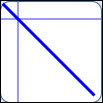 as in $\,y = -x\,$
as in $\,y = -x\,$
|
as $x\rightarrow\infty\,,$ $\,y\rightarrow 3$
Read as:
‘as $\,x\,$ goes to infinity, $\,y\,$ approaches $\,3\,$’
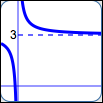 as in $\displaystyle\,y = 3 + \frac 1x$
as in $\displaystyle\,y = 3 + \frac 1x$
|
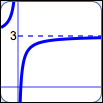 as in $\displaystyle\,y = 3 - \frac 1x\,$
as in $\displaystyle\,y = 3 - \frac 1x\,$
|
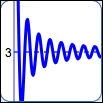 as in $\displaystyle\,y = 3 + \frac{\sin x}{x}\,$
as in $\displaystyle\,y = 3 + \frac{\sin x}{x}\,$
|
End Behavior of Polynomials
Polynomials can't exhibit the full variety of end behavior illustrated above. As $\,x\,$ gets large, $\,y\,$ can only do two things: go to infinity, or go to negative infinity. The best news is that we only need one term of the polynomial to figure out what the end behavior is!
For large values of $\,x\,,$ a polynomial ‘behaves like’ its highest power term.
For example, suppose you're investigating the end behavior of: $$P(x) = x^3 - 3x^2 + 5x - 10$$
Notice that:
- the degree of $\,P\,$ is $\,3\,$
- the leading coefficient is $\,1\,$
- the highest power term is $\,x^3\,$
To investigate the end behavior of $\,P\,,$ you can instead work with the much simpler polynomial $\,Q(x) = x^3\,.$
Why? A renaming of $\,P(x)\,$ does the trick, where we factor out the highest power of $\,x\,$:
$$ \begin{align} P(x) &= \cssId{s61}{x^3 - 3x^2 + 5x - 10}\cr\cr &= \cssId{s62}{x^3\left(1 - \frac 3x + \frac 5{x^2} - \frac{10}{x^3}\right)} \end{align} $$From this new name, it is clear that as $\,x\,$ gets big, all the terms go to zero except the highest power term. Roughly, the highest power term ‘washes out’ all the other terms when $\,x\,$ is big.
Think about this. Even when $\,x\,$ is as small as $\,x = 50\,,$ let's investigate each of the terms in $\,P(x)\,$:
- $x^3 = 50^3 = 125000$
- $-3x^2 = -3\cdot 50^2 = -7500$
- $5x = 5\cdot 50 = 250$
- $-10$
- $P(50) = 125000 {-} 7500 + 250 - 10$
How significant are those other terms compared to the first? Not! The highest power term determines the behavior of the output when the input is large.
The leading coefficient and degree of a polynomial determine its end behavior.
All possible end behaviors of polynomials are summarized in the following table.
End Behaviors of PolynomialsConsider a polynomial with degree $\,n\,$ and leading coefficient $\,a\,.$ Thus, the highest power term is $\,ax^n\,.$ |
|||||
| Degree ($\,n\,$): | $n$ even: $\,n = 2,\, 4,\, 6,\, \ldots$ | ||||
| Leading coefficient ($\,a\,$): | $a \gt 0$ | ||||
| Example: |
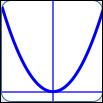 as in $\,y = 3x^2\,$:
$a = 3\,,$ $n = 2$
as in $\,y = 3x^2\,$:
$a = 3\,,$ $n = 2$
|
||||
| End behavior: |
|
||||
| Leading coefficient ($\,a\,$): | $a \lt 0$ | ||||
| Example: |
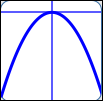 as in $\,y = -3x^2\,$:
$a = -3\,,$ $n = 2$
as in $\,y = -3x^2\,$:
$a = -3\,,$ $n = 2$
|
||||
| End behavior: |
|
||||
| Degree ($\,n\,$): | $n$ odd: $\,n = 1,\, 3,\, 5,\, \ldots$ | ||||
| Leading coefficient ($\,a\,$): | $a \gt 0$ | ||||
| Example: |
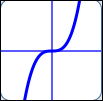 as in $\,y = 2x^3\,$:
$a = 2\,,$ $n = 3$
as in $\,y = 2x^3\,$:
$a = 2\,,$ $n = 3$
|
||||
| End behavior: |
|
||||
| Leading coefficient ($\,a\,$): | $a \lt 0$ | ||||
| Example: |
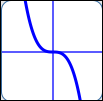 as in $\,y = -2x^3\,$:
$a = -2\,,$ $n = 3$
as in $\,y = -2x^3\,$:
$a = -2\,,$ $n = 3$
|
||||
| End behavior: |
|
||||
Example
Let $\,P(x) = 2x^3 - 5x^7 + 6x - 5\,.$ Determine the end behavior of $\,P\,.$
Solution: The highest order term is $\,-5x^7\,.$ For large values of $\,x\,,$ $\,P(x)\approx -5x^7\,.$
Think of substituting a large positive number into $\,-5x^7\,.$ The sign of the output is: $$\cssId{s124}{(-)(+)^7 = (-)}$$ The output is a large negative number, so:
as $\,x\rightarrow\infty\,,$ $\,P(x)\rightarrow -\infty$
Think of substituting a large negative number into $\,-5x^7\,.$ The sign of the output is: $$\cssId{s129}{(-)(-)^7 = (-)(-) = (+)}$$ The output is a large positive number, so:
as $\,x\rightarrow-\infty\,,$ $\,P(x)\rightarrow \infty$
Making End Behavior Precise
Mathematical sentences like ‘as $\,x\rightarrow\infty\,,$ $\,y\rightarrow\infty\,$’ can be made precise in a Calculus course. For those of you who are curious right now:
$\text{as } x\rightarrow\infty,\ y\rightarrow\infty$
is equivalent to
for every $\,N \gt 0\,$
there exists $\,M \gt 0\,$
such that whenever $\,x \gt M\,,$
$y \gt N$