Work Problems: Quick-and-Easy Estimates
The prior section covered Work Problems: Basic Concepts.
You'll learn to get exact answers in the next section, Work Problems: Guided Practice.
This current section discusses important estimating techniques for work problems.
A Typical Work Problem
Carol mows a lawn in 5 hours.
Julia mows the same lawn in only 3 hours.
How long will it take if they mow the lawn together?
What's the punchline? Together, the time it will take Carol & Julia to mow the lawn together must be between $\,\frac 12(5) = 2.5\,$ hours and $\,\frac 12(3) = 1.5\,$ hours. Why? Keep reading!
Quick-and-Easy Estimates for Work Problems
Getting exact answers to work problems usually involves tools like adding fractions, renaming fractions, and solving equations. However, you can often get in-your-head quick-and-easy estimates!
When possible, you should definitely do this, because it can catch silly mistakes and give confidence in your answers. As is typical for work problems, the Individual Rates Assumption must be true.
This intuitive fact is used in several of the estimates:
Suppose two people take exactly the same time to complete a job. When working together, this time is cut in half.
Why? If you do one job in time $\,T\,,$ then you do half a job in time $\,\frac{1}{2}T\,.$ Two people working—two halves make a whole!
The phrase ‘two-person time’ is used as a shorthand for ‘the time it takes to complete the job when two people are working together’.
Estimate based on a Single Time
Suppose two people are working on a job. Suppose you know how long it takes one person to do the job when they work alone. However, you don't know if this is the faster or slower person.
- With a second person working, the job will get done faster.
- If the second person is wicked fast, then the two-person time can be close to zero.
- If the second person is no help at all (takes near-infinite time), then the two-person time will be close to the one-person time.
Summarizing:
If one person can do a job in time $\,p\,,$ then, working with a second person, the job will be completed between times $\,0\,$ and $\,p\,.$
Move the black point!
The black point gives one person's time to complete a job.
The shaded interval shows the possible two-person times.
Estimate based on a FASTER Time
Let $\,T\,$ be the time it takes a faster person, working alone, to complete a job.
- If a second person works at the same rate, the job will be completed in half the time.
- But, the second person is slower. So, it will take more than half the time, working together.
- If the second person is no help at all (takes near-infinite time), then it will still take about time $\,T\,.$
Summarizing:
If a faster person can do a job in time $\,T\,,$ then, working with a second person, the job will be completed between times $\,\frac{1}{2}T\,$ and $\,T\,.$
Move the big green point!
This point gives a faster person's time to complete a job.
The shaded interval shows the possible two-person times.
Estimate based on a SLOWER Time
Let $\,t\,$ be the time it takes a slower person, working alone, to complete a job.
- If a second person works at the same rate, the job will be completed in half the time.
- But, the second person is faster. So, it will take less than half the time, working together.
- If the other person is wicked fast (takes almost no time at all to do the job), then the time to complete the job will be close to zero!
Summarizing:
If a slower person can do a job in time $\,t\,,$ then, working with a second person, the job will be completed between times $\,0\,$ and $\,\frac{1}{2}t\,.$
Move the big red point!
This point gives a slower person's time to complete a job.
The shaded interval shows the possible two-person times.
Estimate based on BOTH Individual Times
Suppose we know the times it takes both people, working alone, to complete a job. Call these two times $\,T\,$ and $\,t\,.$
If the times are different:
- Call the bigger time $\,t\,.$ Time $\,t\,$ corresponds to the slower worker.
- Call the smaller time $\,T\,.$ Time $\,T\,$ corresponds to the faster worker.
Using the estimates already derived:
- Based on the faster worker, the job must be completed in the time interval $[\frac{1}{2}T,T\,]\,$.
- Based on the slower worker, the job must be completed in the time interval $[0,\frac{1}{2}t]\,$.
So, the two-person time must be in both of these intervals!
Since $\,T\le t\,,$ we have $\,\frac 12T\le \frac 12t\,.$
This fact tells us some important things:
- The intervals $[\frac{1}{2}T,T\,]\,$ and $[0,\frac{1}{2}t]\,$ will always overlap.
- The two-person time is always between $\,\frac{1}{2}T\,$ and $\,\frac{1}{2}t\,.$ (But—sometimes we can do better than this—keep reading!)
- The best estimate for the two-person time is the overlap (intersection) of the two intervals $[\frac{1}{2}T,T\,]\,$ and $[0,\frac{1}{2}t]\,.$
What does the overlap of the intervals $[\frac{1}{2}T,T\,]\,$ and $[0,\frac{1}{2}t]\,$ look like?
It can look two different ways, as shown below. The changing-point in behavior is when the slower time ($\,t\,$) is twice the faster time ($\,T\,$):
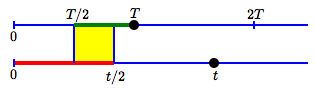
$t < 2T\,$:
overlap
is between
$\frac{T}{2}\,$ and $\,\frac{t}{2}$
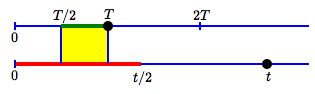
$t > 2T\,$:
overlap
is between
$\frac{T}{2}\,$ and $\,T$
Set your two times by moving the black points.
The green interval shows the possible two-person times
based on the faster time alone.
The purple interval is from
half the faster time to half the slower time.
The red interval shows the possible two-person times
based on the slower time alone.
The best two-person time
estimate is between the dashed lines!
It's a bit of a pain to have to think of the intersection of two intervals when trying to get a quick-and-easy estimate.
Here's a shortcut to finding the best estimate when you know the times for both workers:
- Cut both times in half; the two-person time must be between these two numbers.
- The two-person time must also be less than the fastest time.
Put these two considerations together. Fast and easy!
Here are examples:
-
Carol does a job in $\,5\,$ hours. Julia does the job in $\,3\,$ hours.
The two-person time is between $\,\frac{5}{2} = 2.5\,$ hrs and $\,\frac{3}{2} = 1.5\,$ hrs. (They're both less than $\,3\,.$ Check!)
-
Ray does a job in $\,4\,$ hours. Fred does the job in $\,9\,$ hours.
The two-person time is between $\,\frac{4}{2} = 2\,$ hrs and $\,\frac{9}{2} = 4.5\,$ hrs. The two-person time must also be less than $\,4\,$ hours. Together, the two-person time is between $\,2\,$ hrs and $\,4\,$ hrs.
Don't Mix up Rates and Times!
One final caution—don't fall into the trap of mixing up rates and times.
- When a time is big, then the corresponding rate will be small. Big times correspond to SLOW workers. Small rates correspond to SLOW workers.
- When a time is small, then the corresponding rate will be big. Small times correspond to FAST workers. Big rates correspond to FAST workers.
Here's an example. Suppose Carol completes a job in $\,7\,$ minutes.
- ‘$\,7\,$ minutes’ is a time
- ‘One job per $\,7\,$ minutes’ (or $\,\frac{1\text{ job}}{7\text{ min}}\,$ or $\,\frac 17\ \frac{\text{job}}{\text{min}}\,$) is the corresponding rate
The numbers $\,7\,$ and $\,\frac 17\,$ are reciprocals. If a number is big, its reciprocal is small. If a number is small, its reciprocal is big. You need to keep track of whether you're working with times or rates, because they behave very differently!
Under the Individual Rates Assumption, rates will combine. But, times don't combine!
For example, suppose it takes Ray $\,5\,$ minutes to do the same job that Carol does in $\,7\,$ minutes.
- Carol's rate is $\displaystyle\,\frac{1\text{ job}}{7\text{ min}} = \frac 17\ \frac{\text{job}}{\text{min}}\,$
- Ray's rate is $\displaystyle\,\frac{1\text{ job}}{5\text{ min}} = \frac 15\ \frac{\text{job}}{\text{min}}\,$
The combined rate will be:
$$ \begin{align} &\frac{1}{7}\frac{\text{job}}{\text{min}} + \frac{1}{5}\frac{\text{job}}{\text{min}}\cr\cr &\qquad=\ \frac{5}{35}\frac{\text{job}}{\text{min}} + \frac{7}{35}\frac{\text{job}}{\text{min}}\cr\cr &\qquad=\ \frac{12}{35} \frac{\text{job}}{\text{min}} \end{align} $$However, working together, the time definitely won't be $\,5 + 7\,$ minutes! Indeed, using the quick-and-easy estimate from above, the two-person time must be between $\,\frac 12(5) = 2.5\,$ minutes and $\,\frac{1}{2}(7) = 3.5\,$ minutes.
The next section shows how to get the exact answer.