Relatively Prime Numbers and Related Concepts

For ease of notation, in this section ‘number’ refers to a counting number:   $\,1,\, 2,\, 3,\, \ldots\,$

The prime factorization of a number reveals its ‘multiplicative building blocks’— Jo Johansen uses the words ‘personality’ and ‘structure’ to refer to the prime factorization. The terms ‘unrelated’, ‘lives-in’, and ‘overlapping’ (below) are also credited to Jo. I love the images that this language connotes!

Jo has given me permission to share her insights about how ‘numbers converse with each other due to their personalities’ which gives ‘an efficient set of eyes through which the least common multiple (of two numbers) can be found expeditiously’.

There are three possible ways that two numbers can ‘relate’ to each other:

• relatively prime (unrelated, strangers)
• lives-in
• overlapping

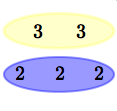
$8\,$ and $\,9\,$ are relatively prime
$8\,$ and $\,9\,$ are unrelated
$8\,$ and $\,9\,$ are strangers

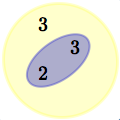
$6$ lives in $18$

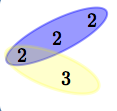
$6\,$ overlaps $\,8\,$

Relatively Prime

Two numbers are relatively prime (informally: ‘unrelated’ or ‘strangers’) when they have no prime factor in common.

Examples

$8 = 2^3\,$ and $\,9 = 3^2\,$ are relatively prime (see image at right). They share no factor except $\,1\,.$ $3\,$ and $\,5\,$ are unrelated. Their greatest common factor is $\,1\,.$ $7\,$ and $\,10\,$ are strangers. The only number that goes into both evenly is $\,1\,.$

$8\,$ and $\,9\,$ are relatively prime $8\,$ and $\,9\,$ are unrelated $8\,$ and $\,9\,$ are strangers

When two numbers are relatively prime (unrelated, strangers), then their least common multiple is their product:

• The least common multiple of $\,8\,$ and $\,9\,$ is $\,8\cdot 9 = 72\,.$
• $\text{lcm}(3,5) = 3\cdot 5 = 15\,$
• $\displaystyle\frac 17 + \frac1{10} = \frac{10}{70} + \frac{7}{70} = \frac{17}{70}$

  Note that the Least Common Denominator (LCD), one important use of the Least Common Multiple (LCM), is $\,7\cdot 10 = 70\,.$

Relatively prime is an important mathematical concept, and hence deserves a formal definition:

Lives-In

The ‘lives-in’ relationship says that one of the structures lives entirely inside the other. That is, one of the numbers contains all the prime factors of the other . It's easy to recognize the lives-in case, because the smaller number goes into the bigger one evenly.

Examples

$6\,$ lives in $\,18\,$ (see image at right). The number $\,18\,$ contains all the prime factors of $\,6\,.$ $3\,$ lives in $\,12\,.$ The number $\,12\,$ is divisible by $\,3\,.$ $15\,$ lives in $\,30\,.$ The number $\,30\,$ is a multiple of $\,15\,.$

$18 = 2\cdot 3\cdot 3$ $6 = 2\cdot 3$ $6\,$ ‘lives in’ $\,18$

In the ‘lives-in’ case, the least common multiple is the bigger number. It's as if the larger number says: ‘Not to worry! I've got you covered, so I'll take care of the least common multiple!’

• the least common multiple of $\,6\,$ and $\,18\,$ is $\,18\,$
• $\text{lcm}(3,12) = 12\,$
• $\displaystyle\frac 1{30} + \frac1{15} = \frac{1}{30} + \frac{2}{30} = \frac{3}{30} = \frac{1}{10}$
  
  Note that the LCD—an important use of the LCM—is the bigger number ($\,30\,$).

Overlapping

In the overlapping case, the structures share information between them, but one does not live in the other.

How can you recognize this case? Firstly, it's not lives-in, so the smaller number doesn't go into the bigger evenly. However, there is at least one prime factor that goes into both numbers evenly.

Example

$6\,$ overlaps $\,8\,$ (see image at right). Note: $\,6\,$ doesn't go into $\,8\,$ evenly. However, $\,2\,$ goes into both $\,6\,$ and $\,8\,$ evenly.

$6 = 2\cdot 3$ $8 = 2\cdot 2\cdot 2$ $6\,$ overlaps $\,8$ shared factor: $\,2\,$ non-shared factors: $\,2\,,$ $\,2\,,$ and $\,3\,$

The least common multiple of two numbers is the product of their shared and non-shared factors. A shared factor is a common factor—it goes into both numbers evenly. A non-shared factor is what's left over after factoring out the common factor.

Here's what it looks like for $\,6\,$ and $\,8\,$:

OR:

Here are more examples of recognizing overlapping numbers and finding their least common multiple:

Practice