Identifying Inequalities with Variables as True or False
An Inequality that is Always True
Consider the inequality ‘$\,x \lt x + 1\,$’. Let $\,x\,$ be any real number. Then, $\,x+1\,$ lies one unit to the right of $\,x\,$ on a number line. Therefore, $\,x\,$ always lies to the left of $\,x+1\,,$ so the sentence ‘$\,x \lt x + 1\,$’ is always true.
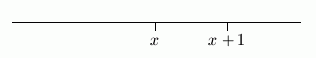
An Inequality that is Always False
Consider the inequality ‘$\,x -1> x\,$’. Let $\,x\,$ be any real number. Then, $\,x-1\,$ lies one unit to the left of $\,x\,$ on a number line. Therefore, $\,x-1\,$ never lies to the right of $\,x\,,$ so the sentence ‘$\,x-1 > x\,$’ is always false.
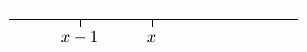
For these exercises, you should think in terms of position on a number line, as in the previous examples.
Examples
Determine if each inequality is ALWAYS TRUE or ALWAYS FALSE.