 Synthetic Division
Synthetic Division
Synthetic division is an efficient shortcut for a special type of division of polynomials problem:
The divisor must be of the form $\,x + c\,$
That is, in the divisor:
- The variable must appear only to the first power ($\,x^1 = x\,$).
- The variable must have a coefficient of $\,1\,$ ($\,x = 1x\,$).
- The number $\,c\,$ can be any real number, but is typically a nonzero integer.
For example, $\,\frac{\text{a polynomial}}{\color{red}{x + 2}}\,$ (here, $\,c = 2\,$) or $\,\frac{\text{a polynomial}}{\color{red}{x - 2}}\,$ (here, $\,c = -2\,$) can be done using synthetic division.
However, $\,\frac{\text{a polynomial}}{\color{red}{3x + 2}}\,$ can't be done using synthetic division, since the coefficient of the $\,x\,$ term must be $\,1\,.$
Also, $\,\frac{\text{a polynomial}}{\color{red}{x^2 + 3}}\,$ can't be done using synthetic division, since the variable is only allowed to be raised to the first power.
Advantages of Synthetic Division
Synthetic division has the following advantages over ‘regular’ long division:
- Only numbers (not variables) are written down
- It uses fewer arithmetic calculations
- It is much more compact (taking less horizontal and vertical space)
- It requires only multiplication and addition, no subtraction (hence is less error-prone)
- It takes less time
Motivation for Synthetic Division
To motivate synthetic division, let's investigate a ‘regular’ long division problem: $$\cssId{s21}{\frac{2x^3 - 5x + 1}{x + 3}}$$ Attention is focused on precisely what numbers are needed in the division process. (The former section, Long Division of Polynomials, can be used for review, as needed.)
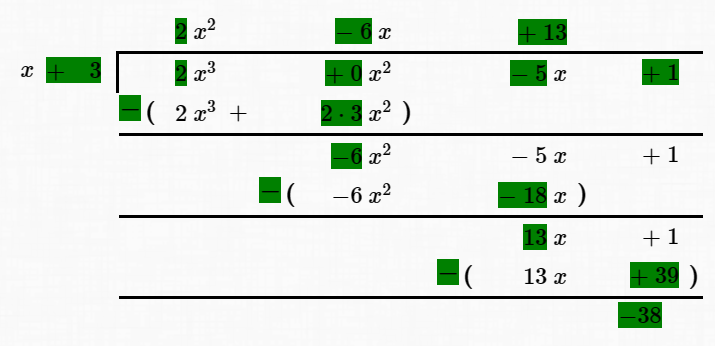
Hover over each yellow-highlighted item below to show what's being talked about in the long-division problem.
| $x$ | $+ \ 3\ $ | $2$ $x^3$ | $+\ 0$ $x^2$ | $-\ 5$ $x$ | $+\ 1$ |
Remember to put in zeros for missing terms. Thus, the number of visible terms in the dividend is always one more than its degree.
Here, the dividend has degree $\,3\,$, and there are $\,4\,$ terms under the long division bar.
| $2$ $x^2$ | |||||||||||||||||
| $x$ | $+ \ 3\ $ | $2$ $x^3$ | $+\ 0$ $x^2$ | $-\ 5$ $x$ | $+\ 1$ | ||||||||||||
| $\bf{-}$ | $\bf{(}$ | $2$ $x^3$ | $+$ | $2\cdot 3$ $x^2$ | $\bf{)}$ | ||||||||||||
| $-6$ $x^2$ | $-\ 5$ $x$ | $+\ 1$ |
The number $\,2\,$ is needed, and is essentially brought up for the first quotient term.
Multiply back: the first term always disappears in the subsequent subtraction.
The second term, which came from $\,2x^2\cdot 3\,,$ is what's important.
Subtract, focusing on the coefficients: $0 - 2\cdot 3 = -6\,.$
Note that:
$0 \overset{\text{subtract}}{\overset{\downarrow}{\ -\ }} 2\cdot 3 = -6$
OR (move the minus sign)
$\,0 \overset{\text{add}}{\overset{\downarrow}{\ +\ }} (-3)\cdot2 = -6$
By changing the sign of the constant term in $\,x + 3\,,$ we can do addition instead of subtraction!
| $2$ $x^2$ | $-\ 6$ $x$ | $+\ 13$ | |||||||||||||||
| $x$ | $+ \ 3\ $ | $2$ $x^3$ | $+\ 0$ $x^2$ | $-\ 5$ $x$ | $+\ 1$ | ||||||||||||
| $\bf{-}$ | $\bf{(}$ | $2$ $x^3$ | $+$ | $2\cdot 3$ $x^2$ | $\bf{)}$ | ||||||||||||
| $-6$ $x^2$ | $-\ 5$ $x$ | $+\ 1$ | |||||||||||||||
| ${\bf{-}}$ | ${\bf{(}}$ | $-6$ $x^2$ | $-\ 18$ $x$ | ${\bf{)}}$ | |||||||||||||
| $13$ $x$ | $+\ 1$ | ||||||||||||||||
| ${\bf{-}}$ | ${\bf{(}}$ | $13$ $x$ | $+\ 39$ | ${\bf{)}}$ | |||||||||||||
| $-38$ |
Finish the problem.
Hover here to see all the important numbers needed in the division problem.
(Want the green to disappear? Then hover here. )
This problem is compared with synthetic division below.
| $-3$ | $2$ | $0$ | $-5$ | $1$ |
| $-6$ | $18$ | $-39$ | ||
| $2$ | $-6$ | $13$ | $-38$ |
| $2$ $x^2$ | $-\ 6$ $x$ | $+\ 13$ | |||||||||||||||
| $x$ | $+ \ 3\ $ | $2$ $x^3$ | $+\ 0$ $x^2$ | $-\ 5$ $x$ | $+\ 1$ |
Here's the same problem, done using synthetic division. More compact, isn't it?!?
The $-3$ represents the divisor, $\,x + 3\,.$ Changing the sign of the constant term allows addition, instead of subtraction.
The row ‘$2$ $0$ $-5$ $1$’ represents the dividend.
The numbers ‘$2$ $-6$ $13$’ represent the quotient. All the digits on this row except the last always represent the quotient.
| $-3$ | $2$ | $0$ | $-5$ | $1$ |
| $-6$ | $18$ | $-39$ | ||
| $2$ | $-6$ | $13$ | $-38$ |
| $2$ $x^2$ | $-\ 6$ $x$ | $+\ 13$ | |||||||||||||||
| $x$ | $+ \ 3\ $ | $2$ $x^3$ | $+\ 0$ $x^2$ | $-\ 5$ $x$ | $+\ 1$ | ||||||||||||
| $\bf{-}$ | $\bf{(}$ | $2$ $x^3$ | $+$ | $2\cdot 3$ $x^2$ | $\bf{)}$ | ||||||||||||
| $-6$ $x^2$ | $-\ 5$ $x$ | $+\ 1$ | |||||||||||||||
| ${\bf{-}}$ | ${\bf{(}}$ | $-6$ $x^2$ | $-\ 18$ $x$ | ${\bf{)}}$ | |||||||||||||
| $13$ $x$ | $+\ 1$ | ||||||||||||||||
| ${\bf{-}}$ | ${\bf{(}}$ | $13$ $x$ | $+\ 39$ | ${\bf{)}}$ | |||||||||||||
| $-38$ |
The number ‘$-38$’ represents the remainder. The last digit on this row always represents the remainder.
These numbers ‘$-6$ $18$ $-39$’ come from here. The process is explained below.
How to Do Synthetic Division: A Step-by-Step Example
Find $$\frac{2x^3 - 5x + 1}{x + 3}$$ using synthetic division.
Step 1: Check Form of Divisor; Identify $\,c\,$
Check that the divisor is of the form $\,x+c\,.$ Identify the number $\,c\,.$ Note that $\,c\,$ is the number that is added to $\,x\,.$
In the divisor $\,x+3\,,$ we have $c = 3\,.$
Step 2: Check the Dividend; Put in Zeros For Missing Terms
Check that the dividend (the numerator) is a polynomial. Write it in standard form, putting in zeroes for any missing terms.
Write the polynomial entirely in terms of addition (no subtractions—use negative coefficients instead).
Step 3: Put the Opposite of $\,c\,$ in a Half-Box; Coefficients of Dividend Next to it
Take the opposite of the number $\,c\,$ identified in step 1; it is used to identify the divisor. (By using the opposite, we do additions instead of subtractions in subsequent steps.)
Put the opposite in a ‘half-box’ as shown below, with the coefficients representing the dividend (from step 2) beside it:
| $-3$ | $2$ | $0$ | $-5$ | $1$ |
Step 4: Draw a Horizontal Line; Bring Down the First Coefficient
Draw a horizontal line below the dividend coefficients, leaving enough vertical space for an additional row of numbers.
Bring down the first coefficient, as shown below:
| $-3$ | $2$ | $0$ | $-5$ | $1$ |
| $2$ |
Step 5: Multiply; Add; Repeat As Needed
Multiply the number in the half-box by the number brought down in the prior step, writing the product beneath the next coefficient: $\,-3\cdot 2 = -6$
| $-3$ | $2$ | $0$ | $-5$ | $1$ |
| $-6$ | $18$ | $-39$ | ||
| $2$ | $-6$ | $13$ | $-38$ |
Add the numbers in the current vertical column, writing the sum below the horizontal line.
Repeat as needed:
- $-3\cdot(-6) = 18\,$
- $-5 + 18 = 13$
- $-3\cdot 13 = -39\,$
- $1 + (-39) = -38$
Step 6: Read Off the Quotient and Remainder
The digits beneath the horizontal line give the quotient and remainder.
| $-3$ | $2$ | $0$ | $-5$ | $1$ |
| $-6$ | $18$ | $-39$ | ||
| $2$ | $-6$ | $13$ | $-38$ |
All digits but the last give the quotient. Start with the power that is one less than the degree of the dividend, and walk on down.
The dividend has degree $\,3\,$; one less than this is $\,2\,.$ Thus, the quotient is $\,2x^2 -6x + 13\,.$
The last digit is the remainder.
Step 7: Summarize the Results
$$ \begin{align} &\cssId{s98}{\frac{2x^3 - 5x + 1}{x + 3}}\cr &\qquad \cssId{s99}{= \text{quotient} + \frac{\text{remainder}}{x + 3}}\cr\cr &\qquad \cssId{s100}{= 2x^2 - 6x + 13 + \frac{(-38)}{x+3}}\cr\cr &\qquad \cssId{s101}{= 2x^2 - 6x + 13 - \frac{38}{x+3}} \end{align} $$
How to do Synthetic Division: An Efficient Example
Use synthetic division to divide $\,\displaystyle x^5 + 3x^3 - 8x^2 - 24\,$ by $\,x-2\,.$ Summarize the results in two equivalent ways.
Step 1: Check Form of Divisor; Identify $\,c\,$
$x - 2 = x + (-2)$
$c = -2$
Step 2: Check the Dividend; Put in Zeros for Missing Terms
$x^5 + 3x^3 - 8x^2 - 24$
$= {\bf 1}x^5 + {\bf 0}x^4 + {\bf 3}x^3 + ({\bf -8}x^2) + {\bf 0}x + ({\bf -24})$
Step 3: Put the Opposite of $\,c\,$ in a Half-Box; Coefficients of Dividend Next to it
| $\ 2\ $ | $1$ | $0$ | $3$ | $-8$ | $0$ | $-24$ |
| $2$ | $4$ | $14$ | $12$ | $24$ | ||
| $1$ | $2$ | $7$ | $6$ | $12$ | $0$ |
Step 4: Draw a Horizontal Line; Bring Down the First Coefficient
Step 5: Multiply; Add; Repeat as Needed
$2\cdot 1 = 2\,$; $0 + 2 = 2$; $2\cdot 2 = 4\,$; $3 + 4 = 7$; $2\cdot 7 = 14\,$; $-8 + 14 = 6$; $2\cdot 6 = 12\,$; $0 + 12 = 12$; $2\cdot 12 = 24\,$; $-24 + 24 = 0$
Step 6: Read Off the Quotient and Remainder
The quotient is $\,x^4 + 2x^3 + 7x^2 + 6x + 12\,.$
The remainder is $\,0\,.$
Step 7: Summarize the Results
$$ \begin{align} &\frac{x^5 + 3x^3 - 8x^2 - 24}{x-2}\cr\cr &\qquad = x^4 + 2x^3 + 7x^2 + 6x + 12 \end{align} $$
Or, equivalently:
$$ \begin{align} &x^5 + 3x^3 - 8x^2 - 24\cr\cr &\qquad = (x^4 + 2x^3 + 7x^2 + 6x + 12)(x-2) \end{align} $$
Note: When $\,x = 0\,,$ substitution into the first equation in step 7 gives $\,\frac{-24}{-2} = 12\,,$ which is true. This gives some confidence in your work.
Substitute $\,x = 0\,$ into the second equation, and see what you get!