Reflecting Property of an Ellipse (Part 2)

(This page is Part 2. Click here for Part 1.)

Physics Principle: the Law of Reflection

Mother Nature is extremely efficient! When light (or sound) travels between two points, it always takes the fastest route. (For light, this is called Fermat's Principle.) In particular, this is true of reflected light.

If the light/sound is always traveling through the same medium (like air), then the fastest route is also the shortest route.

The well-known physics Law of Reflection states that when light/sound is reflected, the angles made with the reflecting surface must be equal.

By the Point/Line/Point Equivalence, equal angles minimizes the distance $\,d(P_1,W) + d(P_2,W)\,$ over all points $\,W\,$ on the line.

Make sure you understand what is being said here! You can certainly draw line segments that go from $\,P_1\,$ to $\,W\,$ to $\,P_2\,,$ where $\,m_1 \ne m_2\,.$ However, this wouldn't be a picture of reflected light. If it's reflected light, then the angles must be the same!

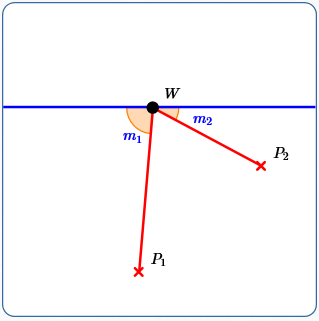
$m_1\ne m_2$
Definitely not reflected light

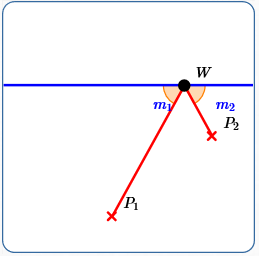
Reflected light
$m_1 = m_2$
(Minimizing the length of the red path over all points $\,W\,$ on the line)

Sum of Distances to Foci for Points Inside, Outside, and On an Ellipse

Here's the final idea that's needed, before putting everything together.

Consider an ellipse with ellipse constant $\,k\,$ and foci $\,F_1\,$ and $\,F_2\,.$ Let $\,P\,$ be a typical point in the plane containing the ellipse.

Point On the Ellipse

When $\,P\,$ is on the ellipse: $$d(F_1,P) + d(F_2,P) = k$$

This is true by the definition of an ellipse.

Point Outside the Ellipse

When $\,P\,$ is outside the ellipse: $$d(F_1,P) + d(F_2,P) \gt k$$

Point Inside the Ellipse

It's also true that:

When $\,P\,$ is inside the ellipse: $$d(F_1,P) + d(F_2,P) \lt k$$

However, this fact isn't needed to prove the ellipse reflecting property.

Playing With Points Inside/Outside/On an Ellipse

These facts are fairly intuitive: small changes in point locations should produce small changes in the distances involved.

Also, you can see these facts ‘in action’ in the exploration below: drag the point $\,P\,$ outside/on/inside the ellipse, observing the displayed sum of the distances.

If desired, move the foci and/or change the ellipse constant via the slider, and explore again!

The facts are also easy to prove, as follows.

Proof: Sum of Distances to Foci for Point Outside an Ellipse

Let $\,P\,$ be outside an ellipse with ellipse constant $\,k\,,$ as shown below.

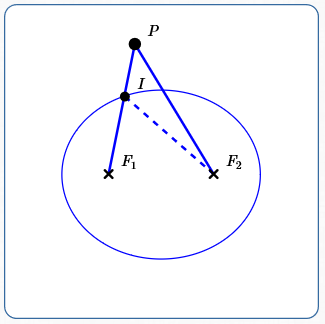
Then: traveling from $\,F_1\,$ to $\,P\,$ to $\,F_2\,$ is longer than traveling from $\,F_1\,$ to $\,I\,$ to $\,F_2\,$ (which equals $\,k\,$).

Here are the details:

Let $\,I\,$ be the point where $\,\overline{PF_1}\,$ intersects the ellipse.
Since $\,I\,$ is on the ellipse: $$d(F_1,I) + d(F_2,I) = k$$
Since the shortest distance between two points is a straight line: $$\cssId{s46}{d(I,P) + d(F_2,P) \gt d(F_2,I)}$$
Combining results: $$ \begin{align} &\cssId{s48}{d(F_1,P) + d(F_2,P)}\cr\cr &\quad\cssId{s49}{= \bigl(\,d(F_1,I) + d(I,P)\,\bigr) + d(F_2,P)}\cr &\qquad\cssId{s50}{\text{(break $\,\overline{F_1P}\,$ into two pieces)}}\cr\cr &\quad\cssId{s51}{= d(F_1,I) + \bigl(\,d(I,P) + d(F_2,P)\,\bigr)}\cr &\qquad\cssId{s52}{\text{(regroup)}}\cr\cr &\quad\cssId{s53}{> d(F_1,I) + d(F_2,I)}\cr &\qquad\cssId{s54}{\text{(use step 3 above)}}\cr\cr &\quad\cssId{s55}{= k}\cr &\qquad\cssId{s56}{\text{(use step 2 above)}} \end{align} $$

Note: The formatting

$$ \begin{align} A &= B\cr &= C\cr &\gt D\cr &= E \end{align} $$

is a shorthand for

$$ \begin{gather} A = B\cr \text{and}\cr B = C\cr \text{and}\cr C \gt D\cr \text{and}\cr D = E \end{gather} $$

from which one concludes that $\,A \gt E\,.$

Proof: Sum of Distances to Foci for Point Inside an Ellipse

Next, let $\,P\,$ be inside an ellipse with ellipse constant $\,k\,,$ as shown below.

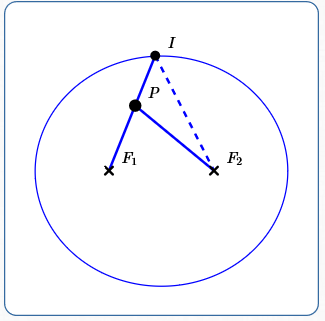
Then: traveling from $\,F_1\,$ to $\,P\,$ to $\,F_2\,$ is shorter than traveling from $\,F_1\,$ to $\,I\,$ to $\,F_2\,$ (which equals $\,k\,$).

Here are the details:

Let $\,I\,$ be the point where $\,\overrightarrow{F_1P}\,$ intersects the ellipse.
Since $\,I\,$ is on the ellipse: $$d(F_1,I) + d(F_2,I) = k$$
Since the shortest distance between two points is a straight line: $$\cssId{s65}{d(F_2,P) \lt d(P,I) + d(F_2,I)}$$
Combining results:
$$ \begin{align} &\cssId{s67}{d(F_1,P) + d(F_2,P)}\cr\cr &\quad\cssId{s68}{< d(F_1,P) + \bigl(\,d(P,I) + d(F_2,I)\,\bigr)}\cr &\qquad\cssId{s69}{\text{(use step 3 above)}}\cr\cr &\quad\cssId{s70}{= \bigl(\,d(F_1,P) + d(P,I)\,\bigr) + d(F_2,I)}\cr &\qquad\cssId{s71}{\text{(regroup)}}\cr\cr &\quad\cssId{s72}{= d(F_1,I) + d(F_2,I)}\cr &\qquad\cssId{s73}{\text{(combine two pieces to get $\,\overline{F_1I}\,$)}}\cr\cr &\quad\cssId{s74}{= k}\cr &\qquad\cssId{s75}{\text{(use step 2 above)}} \end{align} $$

Note: The formatting

$$ \begin{align} A &\lt B\cr &= C\cr &= D\cr &= E \end{align} $$

is a shorthand for

$$ \begin{gather} A \lt B\cr \text{and}\cr B = C\cr \text{and}\cr C = D\cr \text{and}\cr D = E \end{gather} $$

from which one concludes that $\,A \lt E\,.$

Putting It All Together

With all the prior facts in place, it's now easy to understand the ellipse reflecting property. It must be shown that light emitted from one focus is reflected through the other focus.

Refer to the sketch below as you read.

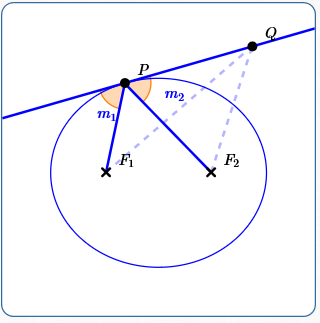
proving the reflecting property of an ellipse

Consider an ellipse with foci $\,F_1\,$ and $\,F_2\,$ and ellipse constant $\,k\,.$

Suppose that light is emitted from $\,F_1\,$ and hits the ellipse at an arbitrary point $\,P\,.$

Draw the tangent line to the ellipse at $\,P\,.$ All points on this tangent line, except $\,P\,$ itself, lie outside the ellipse. This tangent line is the ‘wall’ off of which light reflects.

As shown below, let $\,m_1\,$ denote the measure of the angle between $\,\overline{F_1P}\,$ and the tangent line.

By the Law of Reflection, reflected light must create equal angles with this tangent line.

As shown above, let $\,m_2\,$ denote the measure of the angle between $\,\overline{F_2P}\,$ and the tangent line.

It suffices to show that $\,m_1 = m_2\,.$ In other words, it suffices to show that the angle that $\,\overline{F_2P}\,$ creates with the tangent line is consistent with the behavior of reflected light.

By the ellipse property: $$d(F_1,P) + d(F_2,P) = k$$

Let $\,Q\,$ denote a point on the tangent line.

For $\,Q\ne P\,,$ $\,Q\,$ is outside the ellipse, so that: $$d(F_1,Q) + d(F_2,Q) \gt k$$

Therefore, for every point $\,Q\,$ on the tangent line:

$$ \begin{align} &\overbrace{d(F_1,P) + d(F_2,P)}^{=\ k}\cr &\quad\le \overbrace{d(F_1,Q) + d(F_2,Q)}^{\ge\ k} \end{align} $$

Therefore, point $\,P\,$ minimizes the sum $\,d(F_1,Q) + d(F_2,Q)\,$ over the entire tangent line.

By the Point/Wall/Point Equivalence, $\,m_1 = m_2\,.$ Thus, the path from $\,F_1\,$ to $\,P\,$ to $\,F_2\,$ is the path that reflected light takes, which is what we set out to show!