Getting an Ellipse by Stretching/
This lesson is optional in the Precalculus course.
This lesson assumes knowledge of Equations of Ellipses in Standard Form: Foci on the $x$-axis.
You may find yourself thinking that an ellipse looks like a ‘deformed circle’: you know, just grab the ‘ends’ and stretch or compress the circle. And—you'd be correct, as this lesson shows!
By using earlier work on horizontal and vertical stretching/shrinking of graphs, we get the equation $\,\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1\,$ easily, as follows:
Horizontal Stretch/
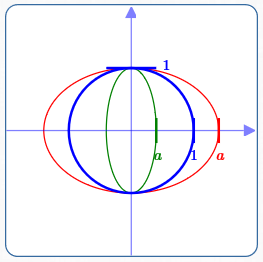
Circle of radius $\,1\,,$ in blue:
$x^2 + y^2 = 1$
Horizontal stretch, in red:
$\displaystyle\frac{x^2}{a^2} + y^2 = 1\,,$ for $\,a \gt 1$
Horizontal shrink, in green:
$\displaystyle\frac{x^2}{a^2} + y^2 = 1\,,$ for $\,0 \lt a \lt 1$
Start with the circle of radius $\,1\,,$ centered at the origin, which has equation $\,x^2 + y^2 = 1\,.$
Replace every $\,x\,$ in the circle equation by $\displaystyle\,\frac xa\,$:
$$ \begin{gather} \left(\frac xa\right)^2 + y^2 = 1\cr\cr \frac{x^2}{a^2} + y^2 = 1 \end{gather} $$This moves a point $\,(x,y)\,$ on the circle to a new point $\,(ax,y)\,$ on an ellipse. For example, the point $\,(1,0)\,$ on the circle moves to $\,(a,0)\,$ on the ellipse.
If $\,a \gt 1\,,$ it is a horizontal stretch.
If $\,0 \lt a \lt 1\,,$ it is a horizontal shrink.
Vertical Stretch/
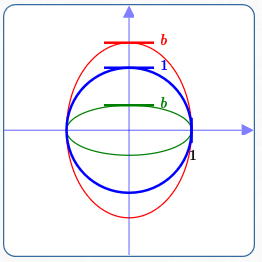
Circle of radius $\,1\,,$ in blue:
$x^2 + y^2 = 1$
Vertical stretch, in red:
$\displaystyle x^2 + \frac{y^2}{b^2} = 1\,,$ for $\,b \gt 1$
Vertical shrink, in green:
$\displaystyle x^2 + \frac{y^2}{b^2} = 1\,,$ for $\,0 \lt b \lt 1$
Similarly, replace every $\,y\,$ with $\,\frac yb\,$ in the equation $\,x^2 + y^2 = 1\,,$ giving the new equation $\,x^2 + \frac{y^2}{b^2} = 1\,.$
This moves a point $\,(x,y)\,$ on the circle to a new point $\,(x,by)\,$ on an ellipse. For example, the point $\,(0,1)\,$ on the circle moves to $\,(0,b)\,$ on the ellipse.
If $\,b \gt 1\,,$ it is a vertical stretch.
If $\,0 \lt b \lt 1\,,$ it is a vertical shrink.
Combined Horizontal/
By replacing both $\,x\,$ by $\,\frac xa\,$ and $\,y\,$ by $\,\frac yb\,,$ we get the equation $\,\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1\,.$
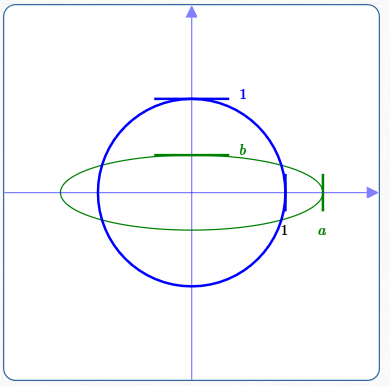
Circle of radius $\,1\,,$ in blue:
$x^2 + y^2 = 1$
Ellipse, in green:
$$\color{green}{\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1}$$
$\,a \gt 1\,,$ Horizontal stretch
$\,0 \lt b \lt 1\,,$ Vertical shrink
A Different (More General) Approach for Transformations Involving $\,y$
People who have thoroughly studied
Horizontal and Vertical Stretching/
In that earlier section, we were dealing with a very specific type of equation involving $\,x\,$ and $\,y\,$: an equation of the form $\,y = f(x)\,.$ Such an equation has $\,y\,$ all by itself on one side; the other side involves only $\,x\,.$
For equations of this special form $\,y = f(x)\,,$ it is easier to treat transformations involving $\,x\,$ and $\,y\,$ differently. We quickly review those differences next:
Transformations Involving $\,y\,$ for Equations of the Form $\,y = f(x)$
Transformations involving $\,y\,$ are intuitive—they work the way you think they should!
The language used is: ‘DO THIS to the previous $y$-value.’
Example: Start with the graph of $\,y = x^2\,.$ Multiply each $y$-value of points on the graph by $\,3\,$ (a vertical stretch). What is the equation of the resulting graph?
Answer:
$\,y = 3x^2$
Multiply the previous $y$-value by $\,3\,.$
In other words:
DO WHAT to the previous
$y$-value?
Answer: Multiply by $\,3\,.$
Transformations Involving $\,x\,$ for Equations of the Form $\,y = f(x)$
Transformations involving $\,x\,$ are not intuitive—they don't work the way you think they should!
The language used is: ‘REPLACE the previous $x$-values by ...’
Example: Start with the graph of $\,y = x^2\,.$ Multiply each $x$-value of points on the graph by $\,3\,$ (a horizontal stretch). What is the equation of the resulting graph?
Answer:
$y = (\frac{x}{3})^2$
Replace every $x$ in the original equation
by $\,\frac{x}{3}\,.$
To get $x$-values in the graph multiplied by $\,3\,,$ we must replace every $\,x\,$ in the equation by $\,\frac{x}{3}\,$ ($\,x\,$ divided by $\,3\,$). Counter-intuitive!
Transformations Involving $\,y\,$ for Equations that are not of the Form $\,y = f(x)$
Sometimes you need to apply graphical transformations to equations that can't be put in the form $\,y = f(x)\,.$
If the graph of an equation doesn't pass a vertical line test, then it can't be put in the form $\,y = f(x)\,.$
The ellipse equation $\,\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1\,$ is such an equation. Its graph doesn't pass the vertical line test. Here, it is possible to solve for $\,y\,,$ but it introduces an annoying square root and ‘plus or minus’ sign.
To apply graphical transformations to any equation in $\,x\,$ and $\,y\,$ (no matter how mixed-up the variables might be), just use the ‘replace every...’ language for both $\,x\,$ and $\,y\,.$
(Then, both cases are equally counter-intuitive!)
For example, if we want every $y$-value in a graph to be multiplied by $\,3\,,$ then replace every $\,y\,$ in the original equation by $\,y\,$ divided by $\,3\,.$
Or, if we want every $y$-value in a graph to be divided by $\,3\,,$ then replace every $\,y\,$ in the original equation by $\,y\,$ multiplied by $\,3\,.$
This more general technique certainly works in the ‘$\,y = f(x)\,$’ case, but isn't needed, as the next example illustrates:
Example
Start with the graph of $\,y = x^2\,.$ Multiply each $y$-value of points on the graph by $\,3\,$ (a vertical stretch). What is the equation of the resulting graph?
Answer: the New Way
Replace every $\,y\,$ by $\,\frac{y}{3}\,,$ giving the new equation:
$$\frac y3 = x^2$$Answer: the Old Way
This is a transformation involving $\,y\,,$ which is intuitive. Multiply the previous $y$-value by $\,3\,,$ giving:
$$y = 3x^2$$They Give the Same Result!
Of course, the equations $\,\frac y3 = x^2\,$ and $\,y = 3x^2\,$ are equivalent!
Just multiply both sides of $\,\frac y3 = x^2\,$ by $\,3\,$ to get $\,y = 3x^2\,.$
There are more details on this ‘new approach’ in a future section.