Equations of Hyperbolas in Standard Form (Part 2)

(This page is Part 2. Click here for Part 1.)

Be Careful!

The variables $\,a\,,$ $\,b\,$ and $\,c\,$ are used for both ellipses and hyperbolas, but their relationship is different!

For ellipses, $\,c^2 = a^2 \color{red}{-} b^2\,.$

For hyperbolas, $\,c^2 = a^2 \color{red}{+} b^2\,.$

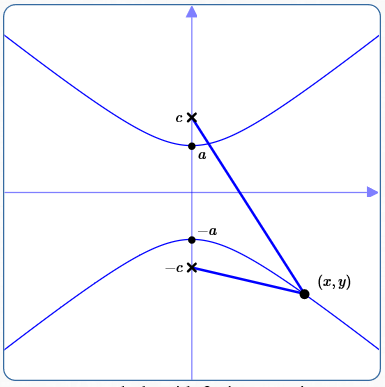
Derivation of the Equation of a Hyperbola: Center at the Origin, Foci on the $y$-axis

The derivation of the equation of a hyperbola with center at the origin and foci on the $y$-axis is nearly identical to the derivation in Part 1.

Position the Hyperbola

As shown above, position a hyperbola with center at the origin and foci (marked with ‘x’) on the $y$-axis. With this positioning, the $y$-axis is the major axis; the $x$-axis is the minor axis.

Notation ($\,c\,$ and $\,a\,$)

Define:

$c := \,$ the distance from the center (the origin) to each focus. Since $\,c\,$ is a distance, $\,c \gt 0\,.$ The coordinates of the foci are therefore $\,(0,c)\,$ and $\,(0,-c)\,.$

$a := \,$ the distance from the center to each vertex. Since $\,a\,$ is a distance, $\,a \gt 0\,$; also, $\,a \lt c\,.$ The coordinates of the vertices are therefore $\,(0,a)\,$ and $\,(0,-a)\,.$

Hyperbola Constant

The hyperbola constant is the distance between the vertices, which is $\,2a\,.$

Summary: Hyperbola Derivation Notation

Hyperbola with foci on $y$-axis and center at the origin

$c := \,$ distance from center to each focus

$a := \,$ distance from center to each vertex

Note that $\,0 \lt a \lt c\,.$

Use the Definition of Hyperbola on a Typical Point

Let $\,(x,y)\,$ be a typical point on the hyperbola. Thus, the difference of its distances to the foci is the hyperbola constant, $\,2a\,.$ That is:

$$ \begin{align} &\biggl|\bigl( \text{distance from } (x,y) \text{ to } (0,-c) \bigr)\cr &\quad - \bigl( \text{distance from } (x,y) \text{ to } (0,c) \bigr)\biggr|\cr &= 2a \end{align} $$

Use the distance formula and make obvious simplications:

$$ \begin{align} &\biggl|\sqrt{(x-0)^2 + \bigl(y-(-c)\bigr)^2}\cr &\quad - \sqrt{\bigl(x - 0\bigr)^2 + \bigl(y-c\bigr)^2}\biggr|\cr &= 2a \end{align} $$
$$ \begin{align} &\biggl|\sqrt{x^2 + (y+c)^2}\cr &\quad - \sqrt{x^2 + (y-c)^2}\biggr|\cr &= 2a \quad (\text{***}) \end{align} $$

Get Rid of the Absolute Values

Recall that for $\,k\ge 0\,,$ $\,|x| = k\,$ is equivalent to $\,x=\pm k\,.$ Use this fact to get rid of the absolute value symbols in (***):

$$ \begin{align} &\sqrt{x^2 + (y+c)^2}\cr &\quad - \sqrt{x^2 + (y-c)^2}\cr &= \pm 2a \quad (\text{****}) \end{align} $$

Don't worry too much about the bothersome ‘plus or minus’ symbol—it will disappear soon!

Apply the ‘Isolate and Undo’ Technique to (****)

We'll choose to isolate the first square root that appears (going from left to right) in (****).

$$ \begin{align} &\sqrt{x^2 + (y+c)^2}\cr &\quad = \pm 2a + \sqrt{x^2 + (y-c)^2} \end{align} $$

Isolate the first square root

$$ \begin{align} &x^2 + (y+c)^2\cr &\quad = \left( \pm 2a + \sqrt{x^2 + (y-c)^2} \right)^2 \end{align} $$

‘Undo’ the isolated square root by squaring both sides

$$ \begin{align} &x^2 + (y+c)^2\cr &\quad = (\pm 2a)^2\cr &\qquad + 2\cdot (\pm 2a)\cdot\sqrt{x^2 + (y-c)^2}\cr &\qquad + \left(\sqrt{x^2 + (y-c)^2}\right)^2 \end{align} $$

FOIL the right-hand side

$$ \begin{align} &x^2 + (y+c)^2\cr &\quad = 4a^2 \pm 4a\sqrt{x^2 + (y-c)^2}\cr &\qquad + x^2 + (y-c)^2 \end{align} $$

Simplify; note that both $\,(2a)^2\,$ and $\,(-2a)^2\,$ give $\,4a^2$

$$ \begin{align} &\color{red}{x^2} + \color{red}{y^2} + 2cy + \color{red}{c^2}\cr &\quad = 4a^2 \pm 4a\sqrt{x^2 + (y-c)^2}\cr &\qquad + \color{red}{x^2} + \color{red}{y^2} - 2cy + \color{red}{c^2} \end{align} $$

FOIL

$$ 2cy = 4a^2 \pm 4a\sqrt{x^2 + (y-c)^2} - 2cy $$

Subtract $\,\color{red}{x^2 + y^2 + c^2}\,$ from both sides

$$ \mp \color{red}{4}a\sqrt{x^2 + (y-c)^2} = \color{red}{4}a^2 - \color{red}{4}cy $$

Isolate the remaining square root term

$$ \mp a\sqrt{x^2 + (y-c)^2} = a^2 - cy $$

Divide by $\,\color{red}{4}$

$$ \left( \mp a\sqrt{x^2 + (y-c)^2}\right)^2 = (a^2 - cy)^2 $$

Square both sides

$$ a^2 \bigl(\ x^2 + (y-c)^2\ \bigr) = (a^2 - cy)^2 $$

Multiply out the left-hand side

$$ \begin{align} &a^2 \bigl(x^2 + y^2 - 2cy + c^2 \bigr)\cr &\quad = a^4 - 2a^2cy + c^2y^2 \end{align} $$

FOIL

$$ \begin{align} &a^2x^2 + a^2y^2 - \color{red}{2a^2cy} + a^2c^2\cr &\quad = a^4 - \color{red}{2a^2cy} + c^2y^2 \end{align} $$

Distributive law

$$ a^2x^2 + a^2y^2 + a^2c^2 = a^4 + c^2y^2 $$

Add $\,\color{red}{2a^2cy}\,$ to both sides

$$ a^2x^2 - c^2y^2 + a^2y^2 = a^4 - a^2c^2 $$

Re-arrange: variable terms on left, constant terms on right

$$ -a^2x^2 + c^2y^2 - a^2y^2 = a^2c^2 - a^4 $$

Multiply both sides by $\,-1$

$$ (c^2 - a^2)y^2 - a^2x^2 = a^2(c^2 - a^2)\qquad (\dagger\dagger) $$

Factor and re-arrange

Notation ($\,b\,$)

Since $\,0 \lt a \lt c\,,$ we have $\,a^2 \lt c^2\,,$ so that $\,c^2 - a^2 \gt 0\,.$

Define $\,b\,$ to be the positive number such that $\,b^2 = c^2 - a^2\,.$ Note that $\,b\,$ is strictly greater than zero.

Rewrite ($\dagger\dagger$) to Eliminate $\,c\,,$ and Simplify

Use $\,b^2 = c^2 - a^2\,$ to rewrite ($\dagger\dagger$):

$$ b^2y^2 - a^2x^2 = a^2b^2 $$

Note that $\,a \gt 0\,$ and $\,b \gt 0\,,$ so $\,ab \gt 0\,$ and hence $\,a^2b^2 \gt 0\,.$ Dividing both sides by $\,a^2b^2\,$ gives:

$$ \begin{gather} \frac{b^2y^2}{a^2b^2} - \frac{a^2x^2}{a^2b^2} = \frac{a^2b^2}{a^2b^2}\cr\cr \frac{y^2}{a^2} - \frac{x^2}{b^2} = 1\cr\cr \end{gather} $$

Summary

The equation of a hyperbola with center at the origin and foci along the $y$-axis is

$$ \frac{y^2}{a^2} - \frac{x^2}{b^2} = 1 $$

where $\,b^2 := c^2 - a^2\,.$

The foci are determined by solving the equation $\,c^2 = a^2 + b^2\,$ for $\,c\,.$ The coordinates of the foci are $\,(0,-c)\,$ and $\,(0,c)\,.$

Summary:  Equations of Hyperbolas with Center at the Origin and Foci on the $x$-axis or $y$-axis

In Both Cases:

$0 \lt a \lt c$

With the equations in standard form, the number $\,a^2\,$ is the denominator of the positive term.

The hyperbola constant is $\,2a\,.$

The foci are determined by solving the equation $\,c^2 = a^2 + b^2\,$ for $\,c\,.$

Be Careful!

The variables $\,a\,,$ $\,b\,$ and $\,c\,$ are used for both ellipses and hyperbolas, but their relationship is different!

For ellipses, $\,c^2 = a^2 \color{red}{-} b^2\,.$

For hyperbolas, $\,c^2 = a^2 \color{red}{+} b^2\,.$

Foci on the $x$-axis

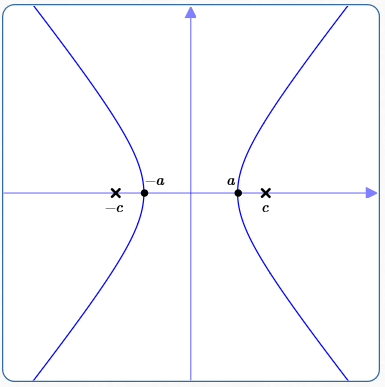
Equation of Hyperbola:

$$\cssId{s23}{\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1}$$

When the foci are on the $\color{red}{x}$-axis, the $\,\color{red}{x^2}$-term is positive.

Coordinates of foci: $\,(-c,0)\,$ and $\,(c,0)$

Foci on the $y$-axis

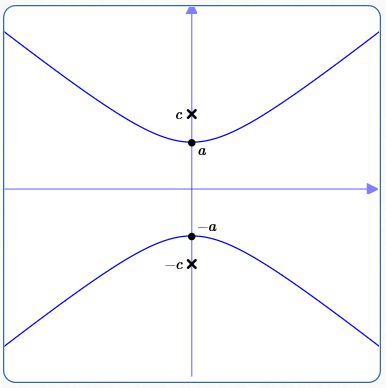
Equation of Hyperbola:

$$\cssId{s30}{\frac{y^2}{a^2} - \frac{x^2}{b^2} = 1}$$

When the foci are on the $\color{red}{y}$-axis, the $\,\color{red}{y^2}$-term is positive.

Coordinates of foci: $\,(0,-c)\,$ and $\,(0,c)$

Tips

The key to recognizing the equation of a hyperbola with center at the origin and foci on either the $x$-axis or $y$-axis is this:

• It has only $\,x^2\,,$ $\,y^2\,,$ and constant terms.
• When the $\,x^2\,$ and $\,y^2\,$ terms are on the same side of the equation, then they must have different signs.

In both equations, the vertices are easy to find. Since the vertices and foci are both on the same axis (the major axis), this is a good way to minimize memorization and let the equation ‘tell you’ where the foci lie:

• Set $\,y = 0\,$ in the equation $\,\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1\,$ to get $\,x = \pm a\,.$ The vertices are on the $x$-axis, hence so are the foci: the major axis is the $x$-axis.
• Set $\,x = 0\,$ in the equation $\,\frac{y^2}{a^2} - \frac{x^2}{b^2} = 1\,$ to get $\,y = \pm a\,.$ The vertices are on the $y$-axis, hence so are the foci: the major axis is the $y$-axis.

To find the foci: With the equations in standard form, $\,c^2\,$ is always the sum of the two denominators:

Example: Finding the Equation of a Hyperbola

Find the Equation of the Following Hyperbola:

• Center at the origin
• Major axis is the $y$-axis, with vertices at $\,\pm 5$
• Containing the point $\,(3,5\sqrt{2})$

Also, find the coordinates of the foci.

Solution

Since the major axis is along the $y$-axis, the form of the equation is:

$\,a = 5\,$

Since $\,(3,5\sqrt{2})\,$ is on the graph:

The equation is:

Foci:

so $\,c = \sqrt{34}\,.$

Coordinates of foci:

(Note that $\,5 \lt \sqrt{34}\,,$ so the foci are ‘inside’ the hyperbola.)