Identifying Conics by the Discriminant (Part 2)

(This page is Part 2. Click here for Part 1.)

Important Notes

Here are additional things you should think about as you study this lesson:

The General Conic Equation is an Equation in Two Variables

Equation ($\,\dagger\,$) is an equation in two variables ($\,x\,$ and $\,y\,$).

The graph of an equation in two variables is the set of all points $\,(x,y)\,$ that make the equation true.

To ‘satisfy the equation’ means to ‘make the equation true’. (Memory device: Being true is a satisfying condition!) If a particular point satisfies the equation, then it's on the graph. If a particular point doesn't satisfy the equation, then it's not on the graph.

Example of a Point Satisfying a General Conic Equation

For example, consider the equation: $$x^2 + xy + y^2 + x + y = 0$$

The point $\,(0,-1)\,$ satisfies this equation, and hence is on the graph of this equation. Why? Substitution of $\,x = 0\,$ and $\,y = -1\,$ into the equation results in a true statement:

$$ \begin{align} &0^2 + (0)(-1) + (-1)^2 + 0 + (-1)\cr &\quad\overset{\text{Yes, it does!}}{=} 0 \end{align} $$

Most Conic Equations Can't be Written in the Form $\,y = f(x)$

Some equations in two variables can be written in the form $\,y = f(x)\,$ (read as: ‘$\,y\,$ equals $\,f\,$ of $\,x\,$’): that is, $\,y\,$ all by itself on one side, with stuff involving only $\,x\,$ (no $\,y\,$) on the other side.

Indeed, this is likely your most common mathematical experience so far: things like $\,y = x^2\,,$ $\,y = \frac{\sqrt{x+1}}{2x-1}\,,$ and $\,y = \sin x + \cos(2x)\,.$

Whenever an equation can be written in the form $\,y = f(x)\,,$ then you're dealing with the graph of a function, which passes a vertical line test. Passing the ‘vertical line test’ means that each (allowable) value of $\,x\,$ has precisely one corresponding value of $\,y\,.$

Most conics don't pass a vertical line test, so they can't be written in the form $\,y = f(x)\,.$ For example, think about the graphs of ellipses—they fail the vertical line test. (Well, except for a ‘point circle’!)

Some Conics Can be Written in the Form $\,y = f(x)$

Here are examples of conics that can be written in the form $\,y = f(x)\,$:

If $\,B = C = 0\,$ and $\,E\ne 0\,,$ then the general conic equation can be rewritten as

$$\,y = \frac{-Ax^2 - Dx - F}{E}$$

(You do the algebra!) These are all parabolas with their axis of symmetry parallel to the $y$-axis.
The equation $\,x^2 + 2xy + y^2 = 0\,$ is equivalent to the line $\,y = -x\,,$ as follows:

$$ \begin{gather} x^2 + 2xy + y^2 = 0\cr (x+y)^2 = 0\cr x + y = 0\cr y = -x \end{gather} $$

This is a degenerate parabola.

‘Extreme’ Solution Sets: The Entire Plane; Nothing

When we defined the general conic equation

$$Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0$$

there were no restrictions placed on the parameters $\,A\,,$ $\,B\,,$ $\,C\,,$ $\,D\,,$ $\,E\,,$ and $\,F\,$ (except that they're real numbers).

Let's take a look at a couple ‘extreme’ cases:

Suppose $\,A = B = C = D = E = F = 0\,,$ so the equation becomes:

$$0x^2 + 0xy + 0y^2 + 0x + 0y + 0 = 0$$

or, more simply:

$$0 = 0$$

What points $\,(x,y)\,$ make this equation true?

Answer: All of them! The graph of this equation is the entire $xy$-plane.
Suppose $\,A = B = C = D = E = 0\,$ and $\,F \ne 0\,,$ so the equation becomes:

$$0x^2 + 0xy + 0y^2 + 0x + 0y + F = 0$$

or, more simply:

$$F = 0$$

Since a nonzero value of $\,F\,$ is not equal to zero, this equation is never true.

There are no points $\,(x,y)\,$ that make the equation true. The graph of this equation is—nothing.

How Can an Entire Plane—or Nothing—Arise as the Intersection of an Infinite Double Cone and a Plane?

When you think about slicing an infinite double cone with a plane, it seems that you'll always get something in the intersection! How is it possible to get an entire plane? Or nothing at all?

To get these two ‘extreme’ cases of ‘conics’ (the entire plane, or nothing), we must allow for limiting cases when constructing the infinite double cone.

Watch this conic video from about 8 seconds to 25 seconds. It shows how an infinite double cone can be generated. (They call it a ‘double right circular cone’.)

Here's what's the video shows:

Start with a point (call it $\,P\,$) on a vertical line.
Pass a second line through $\,P\,.$ This second line is called the generator line.
The generator line rotates about $\,P\,$ to create the infinite double cone.

If the generator line is horizontal, then when it rotates, you get a plane. So, a plane is a limiting case of an infinite double cone.

When you intersect a plane with itself, you get an entire plane. This is the limiting case needed to correspond to the equation ‘$\,0 = 0\,$’.

If the generator line is vertical (so that it coincides with the original vertical line), then the ‘infinite double cone’ degenerates to a single vertical line.

There are lots of vertical planes that won't intersect a given vertical line. This is a limiting case that corresponds to the equation ‘$\,F = 0\,$’, with $\,F\ne 0\,.$

Of course, whenever the generator line is either horizontal or vertical, then you can't get any ‘normal’ ellipses, parabolas, or hyperbolas by intersecting these ‘limiting cases’ of an infinite double cone with a plane.

How Can a Pair of Parallel Lines Arise as the Intersection of an Infinite Double Cone and a Plane?

Short answer—it can't. At least, not from intersecting with a ‘normal’ infinite double cone.

Again, we need a ‘limiting case’ of an infinite double cone; and, we can't get the required limiting case using the cone-generating method from this conic video.

The limiting case we need is an infinite cylinder. (Think of an ‘infinite cylinder’ as an infinite empty paper towel roll.)

Just intersect such a cylinder (see below) with a vertical plane to get a pair of parallel lines.

Here's how to generate an infinite double cone, in order to get an infinite cylinder as a limiting case:

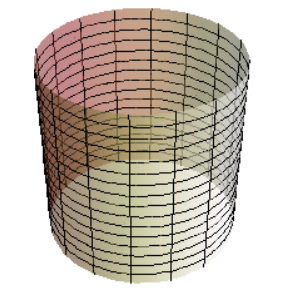
Draw a circle in a horizontal plane.
Draw a vertical line through the center of the circle.
Choose a point (the apex) on this vertical line.
Draw all possible lines connecting the apex to points on the circle.

At this point, you've got a familiar infinite double cone. Now, to get the required limiting case:

Move the apex farther and farther from the circle.
Notice that the lines connecting the apex to the circle get steeper and steeper.
As the apex ‘moves to infinity’, the lines connecting the apex to the circle approach vertical lines. These vertical lines are the sides of the infinite cylinder. This is the desired limiting case.

This ‘infinite cylinder’ goes on forever, both up and down.

This lesson is part of a Precalculus course—it is intended to prepare you for Calculus. The central idea in Calculus is a limit. These discussions of ‘limiting cases’ is a good preview of an essential Calculus idea!