Partial Fraction Expansion: Irreducible Quadratic Factors
Partial Fraction Expansion: Irreducible Quadratic Factors
Partial Fraction Expansion (PFE) renames a fraction of polynomials (i.e., a rational function), using smaller, simpler ‘pieces’.
This is the third of three sections covering PFE:
The first section introduces PFE, reviews all needed concepts, and presents a simple example (distinct linear factors).
The second section gives the complete ‘how-to’ of PFE and a detailed example (repeated linear factor).
This current section presents two detailed examples, both of which illustrate how to handle irreducible quadratic factors:
- PFE with an Initial Long Division, Factoring a Difference of Cubes, and Distinct Irreducible Quadratic Factor
- PFE with a Repeated Irreducible Quadratic Factor
The steps indicated in the examples below follow the summary of the previous section.
Example: PFE with an Initial Long Division, Factoring a Difference of Cubes, and Distinct Irreducible Quadratic Factor
Step 1 (Check Degree of Numerator)
The degree of the numerator ($\,4\,$) is not less than the degree of the denominator ($\,3\,$). Therefore, an initial long division is required, which yields:
In Steps 2–4 below, PFE is applied to the remainder term, $\,\color{green}{\frac{4x^2-3x+2}{x^3-1}}\,.$ In Step 5, we'll need to be sure not to forget the $\,\color{red}{2x}\,$!
Step 2 (Factor Denominator)
The denominator, $\,x^3 - 1\,,$ must be factored into linear factors and irreducible quadratics. The difference of cubes formula comes to the rescue:
$$ \begin{gather} \cssId{s21}{A^3 - B^3} \cssId{s22}{\, = (A - B)(A^2 + AB + B^2)}\cr \cssId{s23}{\text{(The difference of cubes formula)}}\cr\cr \cssId{s24}{x^3 - 1^3} \cssId{s25}{\, = (x - 1)(x^2 + x\cdot 1 + 1^2)}\cr \cssId{s26}{\text{(Apply the formula with $\,A = x\,$ and $\,B = 1\,$)}}\cr\cr \cssId{s27}{x^3 - 1} \cssId{s28}{\, = (x-1)(x^2 + x + 1)}\cr \cssId{s29}{\text{(Simplify)}} \end{gather} $$The factor $\,x-1\,$ is a distinct linear factor. The factor $\,x^2 + x + 1\,$ is a distinct irreducible quadratic factor, since its discriminant is negative:
Step 3 (Form of PFE, With Unknown Constants)
The distinct linear factor, $\,x-1\,,$ gives rise to a single term in the PFE, with a single unknown: say, $\,\frac{A}{x-1}\,.$
The distinct irreducible quadratic factor, $\,x^2 + x +1\,,$ gives rise to a single term in the PFE, with two unknowns: say, $\,\frac{Bx+C}{x^2+x+1}\,.$
Of course, names other than $\,A\,,$ $\,B\,,$ and $\,C\,$ could be used for the unknown constants.
The form of the PFE for $\,\frac{4x^2-3x + 2}{x^3-1}\,$ is therefore:
Step 4 (Clear Fractions; Solve For Unknown Constants)
Clear fractions in ($\,\dagger\,$) by multiplying both sides of the equation by $\,(x-1)(x^2+x+1)\,.$ This gives:
It's always easy to solve for an unknown corresponding to a distinct linear factor. Always get these easy unknowns first!
In this example, the distinct linear factor $\,x-1\,$ corresponds to the term $\,\frac{A}{x-1}\,$ with unknown $\,A\,.$
So, $\,A\,$ is easy to find: let $\,x = 1\,$ in ($\,\ddagger\,$), since this makes $\,x-1\,$ equal to zero:
$$\begin{gather} \cssId{s53}{4\cdot 1^2 - 3\cdot 1 + 2 = A(1^2 + 1 + 1) + 0}\cr\cr \cssId{s54}{3 = A(3)}\cr\cr \cssId{s55}{A = 1} \end{gather} $$It now remains to solve for $\,B\,$ and $\,C\,.$
In what follows, it's important that when you look at $\,(Bx+C)(x-1)\,,$ you actually ‘see’ (in your mind's eye) the multiplied-out version:
(If necessary, multiply it out on paper.)
Thus, $\,B\,$ appears in the coefficients of both $\,x^2\,$ and $\,x\,$ terms. Also, $\,C\,$ appears in the coefficient of an $\,x\,$ term, and in a constant term.
There are choices for how to solve for $\,B\,$ and $\,C\,,$ and some are much better than others!
A few different approaches are shown below—there are many more. It's your job to discover the easy ways! Definitely try to avoid approaches that require solving a system of equations, because these are more error-prone.
The equation that the unknowns ($\,A\,,$ $\,B\,$ and $\,C\,$) must satisfy is repeated here for your convenience:
Here's the same equation with the right-hand side in standard form, so it's easier to compare the coefficients of each term type. In practice, however, try to ‘see’ all this from ($\,\ddagger\,$), without multiplying it out.
Recall that it has already been determined that $\,A = 1\,.$
First Approach (Good)
Equate $\,x^2\,$ coefficients in ($\,\ddagger\,$) to solve for $\,B\,$:
$$ \begin{gather} \cssId{s75}{4 = A + B}\cr \cssId{s76}{4 = 1 + B}\cr \cssId{s77}{\color{green}{B = 3}} \end{gather} $$Equate constant terms in ($\,\ddagger\,$) to solve for $\,C\,$:
$$ \begin{gather} \cssId{s79}{2 = A - C}\cr \cssId{s80}{2 = 1 - C}\cr \cssId{s81}{\color{red}{C = -1}} \end{gather} $$Second Approach (Okay)
Equate constant terms in ($\,\ddagger\,$) to solve for $\,C\,$:
$$ \begin{gather} \cssId{s84}{2 = A - C}\cr \cssId{s85}{2 = 1 - C}\cr \cssId{s86}{\color{red}{C = -1}} \end{gather} $$Equate $\,x\,$ coefficients in ($\,\ddagger\,$) to solve for $\,B\,$:
$$ \begin{gather} \cssId{s88}{-3 = A + C - B}\cr \cssId{s89}{-3 = 1 - 1 - B}\cr \cssId{s90}{-3 = -B}\cr \cssId{s91}{\color{green}{B = 3}} \end{gather} $$Third Approach (Good)
Let $\,x = 0\,$ in ($\,\ddagger\,$):
$$\begin{gather} \cssId{s94}{2 = A - C}\cr \cssId{s95}{2 = 1 - C}\cr \cssId{s96}{\color{red}{C = -1}} \end{gather} $$Equate $\,x^2\,$ coefficients in ($\,\ddagger\,$) to solve for $\,B\,$:
$$ \begin{gather} \cssId{s98}{4 = A + B}\cr \cssId{s99}{4 = 1 + B}\cr \cssId{s100}{\color{green}{B = 3}} \end{gather} $$Fourth Approach (Horrible)
Equate $\,x\,$ coefficients in ($\,\ddagger\,$):
$$ \begin{gather} \cssId{s103}{-3 = A + C - B}\cr \cssId{s104}{-3 = 1 + C - B}\cr \cssId{s105}{-4 = C - B} \end{gather} $$Let $\,x = 2\,$ (arbitrarily chosen) in ($\,\ddagger\,$):
Solve the system of equations:
$$ \begin{gather} \cssId{s112}{-4 = C - B}\cr \cssId{s113}{5 = 2B + C} \end{gather} $$Using substitution, the first equation gives $\,C = -4 + B\,.$
Substitution into the second equation gives $\,5 = 2B - 4 + B\,.$ Solving for $\,B\,$ gives $\,9 = 3B\,,$ so $\,\color{green}{B = 3}\,.$
Then, the first equation gives $\,-4 = C - 3\,,$ so $\,\color{red}{C = -1}\,.$
Of course, all correct approaches will lead to the same results. (The author prefers the first approach.)
Thus, we have:
$$ \cssId{s121}{\frac{4x^2-3x+2}{x^3-1} = \frac{1}{x-1} + \frac{3x-1}{x^2 + x + 1}} $$Step 5 (Summarize Results; Spot-Check)
Combine the results from Step 1 and Step 4 to get:
Spot-check with $\,x = 0\,$ to gain confidence in the result:
$$ \begin{gather} \cssId{s126}{\frac{2}{-1} \overset{?}{=} \frac{1}{-1} + \frac{-1}{1}}\cr\cr \cssId{s127}{-2 = -2}\qquad \cssId{s128}{\text{Hooray!}} \end{gather} $$Example: PFE With a Repeated Irreducible Quadratic Factor
(The following solution is much more compact than the prior example.)
Step 1 (Check Degree of Numerator)
The degree of the numerator ($\,2\,$) is less than the degree of the denominator ($\,4\,$). Check!
Step 2 (Factor Denominator)
The denominator is a ‘fake quadratic’ (also called a ‘pseudo-quadratic’):
The quadratic $\,x^2 + 3\,$ is irreducible. Why? Use any of the following equivalent characterizations:
-
The discriminant is negative:
$$ \begin{align} b^2 - 4ac &= 0^2 - 4(1)(3)\cr &= -12\cr &\lt 0 \end{align} $$
- There are no real number solutions to $\,x^2 + 3 = 0$
- The graph of $\,y = x^2 + 3\,$ never crosses the $x$-axis
Thus, $\,(x^2 + 3)^2\,$ is a repeated irreducible quadratic factor.
Step 3 (Form of PFE, with Unknown Constants)
The repeated irreducible quadratic factor, $\,(x^2 + 3)^\color{red}{2}\,,$ gives rise to two terms in the PFE, each with two unknowns:
Step 4 (Clear Fractions; Solve for Unknown Constants)
Clear fractions in ($\,\dagger\,$) to get:
$$ \cssId{s152}{3x^2 - 5 = (Ax + B)(x^2 + 3) + Cx + D} \qquad \cssId{s153}{(\ddagger)} $$Equate $\,x^3\,$ coefficients in ($\,\ddagger\,$) to get $\,A = 0\,.$
Equate $\,x^2\,$ coefficients in ($\,\ddagger\,$) to get $\,B = 3\,.$
Equate $\,x\,$ coefficients in ($\,\ddagger\,$) to get:
$$\begin{gather} \cssId{s157}{0 = 3A + C}\cr \cssId{s158}{0 = 3(0) + C}\cr \cssId{s159}{C = 0} \end{gather} $$Equate constants in ($\,\ddagger\,$) to get:
$$\begin{gather} \cssId{s161}{-5 = 3B + D}\cr \cssId{s162}{-5 = 3(3) + D}\cr \cssId{s163}{D = -14} \end{gather} $$Step 5 (Summarize Results; Spot-Check)
Thus:
Spot-check with $\,x = 0\,$ to gain confidence in the result:
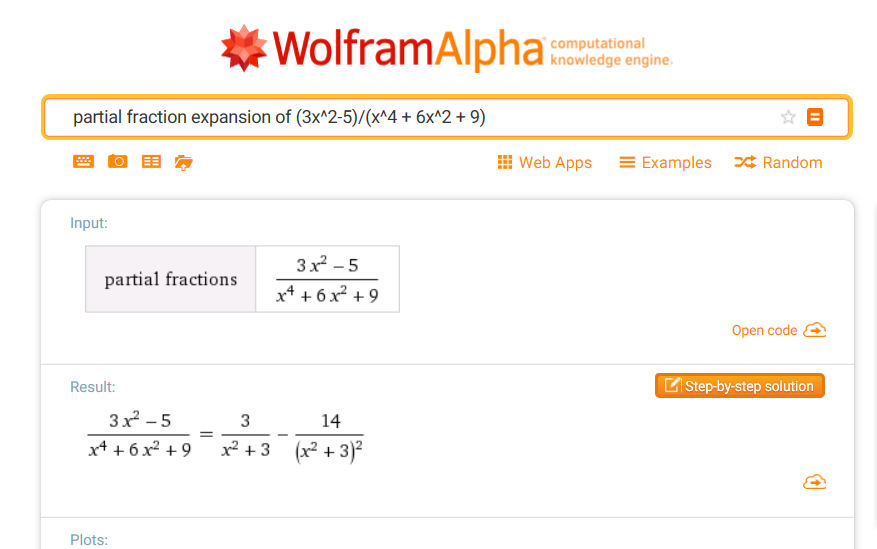
$$ \begin{gather} \cssId{s168}{\frac{-5}{9} \overset{?}{=} \frac{3}{3} - \frac{14}{9}}\cr\cr \cssId{s169}{-\frac 59 = -\frac 59}\cr\cr \cssId{s170}{\text{Hooray!}} \end{gather} $$Or, zip up to WolframAlpha for the ultimate confidence booster: