Equivalence Relations
Suppose students in a class are getting together in groups to do an activity. The teacher wants to make sure of two things:
- no student is in more than one group (i.e., the groups don't overlap), and
- every student is accounted for (i.e., all the groups, together, make up the entire class).
From a mathematical viewpoint, what has been created is a partition of the class:
More precisely, ‘make up all of $\,S\,$’ means that the union of the subsets is $\,S\,.$
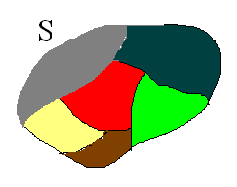A partition of a set $\,S\,$
Examples
The sets $\,\{1,2,3\}\,$ and $\,\{4,5\}\,$ form a partition of $\,S\,$: they don't overlap, and, together, they make up all of $\,S\,.$
The sets $\,\{1,5\}\,$ and $\,\{2,3,4\}\,$ form a different partition of $\,S\,.$
The sets $\,\{1\}\,$ and $\,\{3\}\,$ and $\,\{2,4,5\}\,$ form a different partition of $\,S\,.$
The sets $\,\{1,2\}\,$ and $\,\{3,4\}\,$ do not form a partition of $\,S\,$; together, they don't make up all of $\,S\,.$
The sets $\,\{1,2,3\}\,$ and $\,\{3,4,5\}\,$ do not form a partition of $\,S\,$; they overlap—the number $\,3\,$ is in more than one of the subsets.
The sets $\,\{1,2\}\,$ and $\,\{2,3\}\,$ and $\,\{4,5\}\,$ do not form a partition of $\,S\,$; they overlap—the number $\,2\,$ is in more than one of the subsets.
Being ‘Related To Each Other’ In a Set
One of the most important ways in math to create a partition of a set is by using an equivalence relation, which is the subject of this section.
Given a set $\,S\,,$ we first need a way to talk about members of the set being related to each other. The symbol ‘$\,\sim\,$’ is used for ‘is related to’. The sentence ‘$\,x\sim y\,$’ is read as ‘$\,x\,$ is related to $\,y\,$’.
The concept is best illustrated with some examples:
Same-Sex Relation
Let $\,S\,$ be the set of all people, and let $\,x\,$ and $\,y\,$ be members of $\,S\,.$ Define:
$\,x\sim y\,$
if and only if
$\,x\,$ and $\,y\,$ have the same sex
Suppose that Carol and Julia are female; Rick and Karl are male.
| TRUE SENTENCE | READ AS: | WHY TRUE? |
| Carol $\,\sim \,$ Julia | Carol is related to Julia | both Carol and Julia are female |
| Carol $\,\not\sim\,$ Karl | Carol is not related to Karl | Carol and Karl do not have the same sex |
| Rick $\,\sim \,$ Karl | Rick is related to Karl | both Rick and Karl are male |
Same-Remainder Relation
Let $\,S=\{0,1,2,3,\ldots\}\,.$
For $\,x\,$ and $\,y\,$ in $\,S\,,$ define:
$x\sim y\,$
if and only if
$\,x\,$ and $\,y\,$ have the same remainder
upon division by $\,3\,$
| TRUE SENTENCE | READ AS: | WHY TRUE? |
| $\,5\sim 8\,$ | $\,5\,$ is related to $\,8\,$ |
When $\,5\,$ is divided by $\,3\,,$
the remainder is
$\,2\,$:
$$\cssId{s69}{5 = 1\cdot 3 \color{red}{+ 2}}$$
When $\,8\,$ is divided by $\,3\,,$ the remainder is $\,2\,$: $$\cssId{s71}{8 = 2\cdot 3 \color{red}{+ 2}}$$ Thus, both have the same remainder ($\,2\,$) when divided by $\,3\,.$ |
| $\,3\sim 12\,$ | $\,3\,$ is related to $\,12\,$ |
When $\,3\,$ is divided by $\,3\,,$
the remainder is
$\,0\,$:
$$\cssId{s76}{3 = 1\cdot 3 + 0}$$
When $\,12\,$ is divided by $\,3\,,$ the remainder is $\,0\,$: $$\cssId{s78}{12 = 4\cdot 3 + 0}$$ Thus, both have the same remainder ($\,0\,$) when divided by $\,3\,.$ |
| $\,1\not\sim 11\,$ | $\,1\,$ is not related to $\,11\,$ |
When $\,1\,$ is divided by $\,3\,,$
the remainder is
$\,1\,$:
$$\cssId{s83}{1 = 0\cdot 3 + 1}$$
When $\,11\,$ is divided by $\,3\,,$ the remainder is $\,2\,$: $$\cssId{s85}{11 = 3\cdot 3 + 2}$$ Thus, $\,1\,$ and $\,11\,$ have different remainders when divided by $\,3\,.$ |
Equivalent-Fraction Relation
Let $\,S\,$ be the set of all ordered pairs of positive integers.
For $\,(a,b)\,$ and $\,(c,d)\,$ in $\,S\,,$ define:
$\,(a,b) \sim (c,d) \,$
if and only if
$\,ad=bc\,$
| TRUE SENTENCE | READ AS: | WHY TRUE? |
| $\,(1,3)\sim (2,6)\,$ | $\,(1,3)\,$ is related to $\,(2,6)\,$ | $\,1\cdot 6 = 3\cdot 2\,$ |
| $\,(2,5)\sim (4,10)\,$ | $\,(2,5)\,$ is related to $\,(4,10)\,$ | $\,2\cdot 10 = 5\cdot 4\,$ |
| $\,(1,3)\not\sim (2,5)\,$ | $\,(1,3)\,$ is not related to $\,(2,5)\,$ | $\,1\cdot 5\neq 3\cdot 2\,$ |
(This concept is very familiar to you; it's just being cast into an unfamiliar setting. Hint—think about fractions!)
Equivalence Relations
Now, we are in a position to define an equivalence relation:
Then, $\,\sim \,$ is an equivalence relation on $\,S\,$ if and only if the following properties are satisfied for all members $\,x\,,$ $\,y\,$ and $\,z\,$ in $\,S\,$:
-
REFLEXIVE property:
$\,x\sim x\,$
(every member is related to itself)
-
SYMMETRY property:
if $\,x\sim y\,,$
then $\,y\sim x\,$
(if one member is related to another, then the other is related to the one)
-
TRANSITIVE property:
if $\,x\sim y\,$ and $\,y\sim z\,,$
then $\,x\sim z\,$
(if one is related to another, and this other is related to a third, then the first is related to the third)
Example (An Equivalence Relation on the Set of All People)
(1) Let $\,S\,$ be the set of all people, and let $\,x\,$ and $\,y\,$ be members of $\,S\,.$ Define:
$\,x\sim y\,$
if and only if
$\,x\,$ and $\,y\,$ have the same sex
Then, $\,\sim \,$ is an equivalence relation on $\,S\,,$ as follows:
- Reflexivity: every person has the same sex as his/her self
- Symmetry: if a person has the same sex as another person, then the other person has the same sex as the first
- Transitivity: if person #1 has the same sex as person #2, and person #2 has the same sex as person #3, then person #1 has the same sex as person #3
Example (An Equivalence Relation on the Set of All Nonnegative Integers)
(2) Let $\,S=\{0,1,2,3,\ldots\}\,.$
For $\,x\,$ and $\,y\,$ in $\,S\,,$ define:
$\,x\sim y\,$
if and only if
$\,x\,$ and $\,y\,$
have the same remainder upon division by $\,3\,$
Then, $\,\sim \,$ is an equivalence relation on $\,S\,,$ as follows:
- Reflexivity: every number has the same remainder upon division by $\,3\,$ as itself
- Symmetry: if a number has the same remainder upon division by $\,3\,$ as another, then the other has the same remainder upon division by $\,3\,$ as the first
- Transitivity: if a number has the same remainder upon division by $\,3\,$ as another, and this other has the same remainder upon division by $\,3\,$ as a third, then the first number has the same remainder upon division by $\,3\,$ as the third
Example (NOT An Equivalence Relation)
(3) Let $\,S=\{0,1,2,3,\ldots\}\,.$
For $\,x\,$ and $\,y\,$ in $\,S\,,$ define:
$\,x\sim y\,$
if and only if
$\,x\lt y\,$
Then, $\,\sim \,$ is not an equivalence relation on $\,S\,.$ It fails both reflexivity (since $\,x\,$ is not less than $\,x\,$) and symmetry (if $\,x\,$ is less than $\,y\,,$ then $\,y\,$ is not less than $\,x\,$).
Equivalence Classes
Once you select a member of a set which has an equivalence relation on it, you often want to study all the members which are related to it. This leads us to:
Let $\,\sim \,$ be an equivalence relation on a set $\,S\,.$ Let $\,x\,$ be a member of $\,S\,.$
The equivalence class determined by $\,x\,$ is the set of all members of $\,S\,$ that are related to $\,x\,.$
Here is one key reason why equivalence relations are so important:
The equivalence classes of a set always form a PARTITION of the set.
For Example (1) above, there are only two equivalence classes: males and females.
For Example (2) above, there are three equivalence classes:
-
$\,\{0,3,6,\ldots\}\,$
(numbers that are divisible by $\,3\,$; that is, the remainder is $\,0\,$)
-
$\,\{1,4,7,\ldots\}\,$
(numbers that leave a remainder of $\,1\,$ upon division by $\,3\,$)
-
$\,\{2,5,8,\ldots\}\,$
(numbers that leave a remainder of $\,2\,$ upon division by $\,3\,$)
As a final example, congruence is an equivalence relation on the set of all geometric figures. Let $\,G_1\,,$ $\,G_2\,,$ and $\,G_3\,$ be geometric figures. Then:
- Reflexivity: $\,G_1 \cong G_1$ (every geometric figure is congruent to itself)
- Symmetry: if $\,G_1\cong G_2\,$ then $\,G_2\cong G_1$
- Transitivity: if $\,G_1\cong G_2\,$ and $\,G_2\cong G_3\,,$ then $\,G_1\cong G_3$