Introduction to Area and Perimeter

Simple Closed Plane Curves

Take a piece of paper and a pencil. Put your pencil on the paper and draw anything you want, with the following conditions:

• you must return to your starting point
• you are not allowed to cross over anything you have drawn

The resulting curve is called a simple closed plane curve.

• It is a plane curve because it lies in a plane.
• It is closed because it starts and ends at the same place.
• It is simple because it never crosses itself.

a simple closed plane curve

a simple plane curve, that is not closed

a closed plane curve, that is not simple

a plane curve that is not simple and not closed

not a plane curve
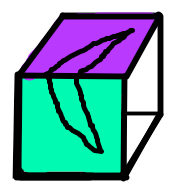(it is drawn on both the front face and the top face)

Every simple closed plane curve has both an inside (the region enclosed by the curve) and an outside (the region not enclosed by the curve). Although this seems like an obvious statement, it is actually quite difficult to prove. Explore the ‘Jordan Curve Theorem’ if you're interested.

When you are asked for the ‘area’ of a simple closed plane curve, this means the area inside the curve. For example, the area of a rectangle is the area inside the rectangle, and the area of a triangle is the area inside the triangle.

Whereas area measures the space ‘inside’ a figure, we can also ask about the distance ‘around’ a figure:

Quite a mouthful! Probably more than you want to hear right now! The definition looks simpler if we specialize it to polygons:

Note that your teacher might ask you to ‘trace a perimeter’—that is, run your finger (or pencil) along a curve. Or, your teacher might ask you to ‘shade an area’—that is, shade the region inside a simple closed plane curve.

Units for Area and Perimeter

Perimeter is measured using units of length. Consequently, these are all valid units for perimeter, with their common abbreviations:

• millimeter  (mm)
• centimeter  (cm)
• meter  (m)
• kilometer  (km)
• inch  (in)
• foot  (ft)
• yard  (yd)
• mile  (mi)

Every unit of length has a corresponding unit of area, created as follows:

• Let ‘$\,1\text{ blah}\,$’ be a unit of length (see below).
• Create a square, where each side has length $\,1\text{ blah}\,.$
• The resulting square has area ‘$\,1\,$ square blah’, which is abbreviated as ‘$\,1{\text{ blah}}^2\,$’.

$\,\text{length} = 1\text{ blah}\,$
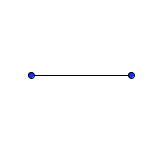a unit of length

$ \cssId{s66}{\text{area} = 1 \text{ square blah}} \cssId{s67}{= 1{\text{ blah}}^2} $
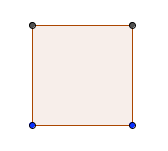a unit of area

Here are some valid units for area, with abbreviations:

• square millimeter  ($\,{\text{mm}}^2\,$)
• square centimeter  ($\,{\text{cm}}^2\,$)
• square meter  ($\,{\text{m}}^2\,$)
• square kilometer  ($\,{\text{km}}^2\,$)
• square inch  ($\,{\text{in}}^2\,$)
• square foot  ($\,{\text{ft}}^2\,$)
• square yard  ($\,{\text{yd}}^2\,$)
• square mile  ($\,{\text{mi}}^2\,$)

Here are some basic formulas:

Area of a Rectangle

A rectangle with length $\,\ell \,$ and width $\,w\,$ has area $\,A\,$ given by $\,A=\ell w\,.$

Area of a Square

A square with sides of length $\,\ell \,$ has area $\,A\,$ given by $\,A=\ell^2\,.$

Perimeter of a Rectangle

A rectangle with length $\,\ell \,$ and width $\,w\,$ has perimeter $\,P\,$ given by $\,P=2\ell + 2w\,.$

Perimeter of a Square

A square with sides of length $\,\ell \,$ has perimeter $\,P\,$ given by $\,P=4\ell\,.$