Beginning Terminology: Points, Lines, and Planes
The word ‘geometry’ derives from the Greek words for ‘earth’ (geo) and ‘to measure’ (metron).
A construction is a geometric drawing for which only a compass and a straightedge may be used. You will study many different constructions in Geometry, many of which are beautifully illustrated here:
Zef Damen Constructions with Ruler and Compass
a compass:
for making circles;
for transferring the distance
between two existing points
ruler/straightedge:
used for drawing a line between two existing points;
no distance markings will be used;
no measurements are allowed
A conjecture is an educated guess.
Using specific observations and examples to arrive at a conjecture is called inductive reasoning. For example, you might make the conjecture that for all real numbers $\,x\,$ and $\,y\,,$ the distance between them is given by the formula $\,y-x\,.$
A counterexample is a specific example that shows that a conjecture is not always true. For example, here is a counterexample to the previous conjecture:
Let $\,y=5\,$ and $\,x=7\,.$ Then, $\,y-x=5-7=-2\,,$ which is not the distance between them.
Deductive reasoning uses logic, and statements that are already accepted to be true, to reach conclusions. The methods of mathematical proof are based on deductive reasoning.
Point, line, and plane are three undefined terms to get us started in the study of geometry—we will just agree on their meaning.
A point represents an exact location. It is represented with a dot. Capital letters, like $\,P\,,$ are frequently used to denote points.
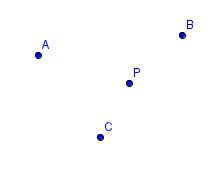
Space is the set of all points.
A geometric figure is a subset of space.
That is, a geometric figure is any collection of points. Of course, there are certain important geometric figures (like triangles and circles) that will be studied throughout the course.
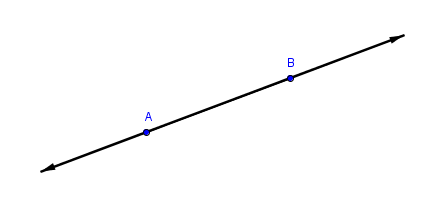
A line has length only; it has no width or thickness; it extends forever in both directions. A line will be denoted using a lowercase script letter, like $\,\ell \,.$
If $\,A\,$ and $\,B\,$ are two distinct points, then they determine a unique line which will be denoted by $\,\overleftrightarrow{AB}\,$ or $\,\overleftrightarrow{BA}\,.$
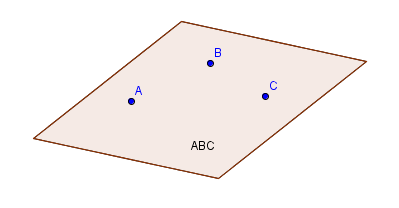
A plane is a flat surface that extends infinitely in all directions; it has length and width only; it has no thickness. A plane will be denoted using an uppercase script letter, like $\,\mathcal{P}\,.$
If $\,A\,,$ $\,B\,,$ and $\,C\,$ are three distinct noncollinear points (see below), then they determine a unique plane which will be denoted by $\,ABC\,.$
Note: In the following definitions, the prefix ‘co’ means ‘same’.
Collinear points: three or more points lying on the same line
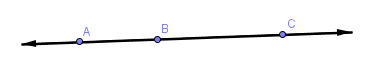
Noncollinear points: points not lying on the same line
Coplanar points: points lying in the same plane
Noncoplanar points: points not lying in the same plane
Coplanar can also refer to other geometric figures. For example, two lines are coplanar if and only if they lie in the same plane.
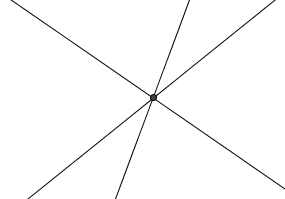
Three or more lines are concurrent if they share a unique common point.
