On this worksheet, you are only given hints to various GeoGebra operations. You will need to figure out how to do some things yourself!

GeoGebra Worksheet:
BISECTING AN ANGLE

GeoGebra an be used to ‘simulate’ a hand construction, by using only the circle and segment tools. This worksheet shows you how.

For comparison purposes, you may also want to bisect an angle using a hand construction:
hand construction: bisecting an angle

COPYING A LINE SEGMENT

Uncheck VIEW-AXES.
Select OPTIONS-LABELING-NEW POINTS ONLY, so that only new points will be labeled.
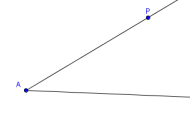
Use the ray tool to create an angle to bisect.
The vertex should be labeled $\,A\,.$
The point on the upper side should be renamed $\,P\,$; this point will be used later to change the original angle.
Hide the point on the lower side.
You should be looking at something like this:
Pick an appropriate radius (say, $\,3\,$) and use the ‘Circle with center and radius’ tool to construct a circle with center $\,A\,.$
Mark the intersections points $\,B\,$ and $\,C\,,$ as shown below.
(Note: The easiest way to get an intersection point is just to click on it!)
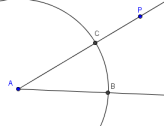
Pick an appropriate radius (say, $\,1.5\,$) and use the ‘Circle with center and radius’ tool to construct two circles, with centers $\,B\,$ and $\,C\,,$ each with this chosen radius.
Mark the (outer) intersection point $\,D\,,$ as shown below:
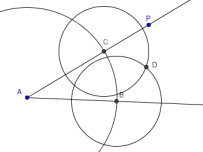
Use the ‘Input:’ field to measure two angles:
mofang1 = angle[D,A,C]
mofang2 = angle[B,A,D]
Note: Angles are measured positive counter-clockwise.
Put in the ray through $\,A\,$ and $\,D\,.$
Clean things up, hiding all auxiliary objects.
Put in the dynamic text shown below:

When you're done with this worksheet,
move on to:
Introduction to the Two-Column Proof