Differentiation Formula Practice

In this lesson, as needed, functions are assumed to be differentiable and to have all required properties.

For example:

Any function in a denominator is assumed to be nonzero.
Any function inside a logarithm is assumed to be positive.
And so on!

This lesson gives practice with all the following differentiation rules:

Slide Constants Out

You can ‘slide constants out’ of the differentiation process:

$$\frac{d}{dx}\bigl( kf(x)\bigr) = k\,\frac{d}{dx} f(x)$$

Or, using prime notation for the derivative on the right side:

$$\frac{d}{dx}\bigl( kf(x)\bigr) = k\,f'(x)$$

Derivative of a Sum

The derivative of a sum is the sum of the derivatives:

$$\frac{d}{dx} \bigl( f(x) + g(x) \bigr) = \frac{d}{dx} f(x) + \frac{d}{dx} g(x)$$

Since subtraction is just adding the opposite, this also works for differences.

Above, Leibniz notation is used on both sides of the equation. The equation can also be written using prime notation on the right:

$$\frac{d}{dx} \bigl( f(x) + g(x) \bigr) = f'(x) + g'(x)$$

Derivative of a Product

The derivative of a product is not the product of the derivatives!

The Product Rule is:

$$\frac{d}{dx}\bigl( f(x)g(x)\bigr) = f(x)g'(x) + g(x)f'(x)$$

Verbalize: the derivative of a product is the first, times the derivative of the second, plus the second, times the derivative of the first.

Some people memorize the formula in a different way (where the order of the factors is preserved):

$$\frac{d}{dx}\bigl( f(x)g(x)\bigr) = f'(x)g(x) + f(x)g'(x)$$

Verbalize: the derivative of a product is the derivative of the first, times the second, plus the first, times the derivative of the second.

Derivative of a Quotient

The derivative of a quotient is not the quotient of the derivatives!

The Quotient Rule is:

$$\frac{d}{dx}\left( \frac{f(x)}{g(x)}\right) = \frac{g(x)f'(x) - f(x)g'(x)}{(g(x))^2}$$

Verbalize: the derivative of a quotient is the bottom, times the derivative of the top, minus the top, times the derivative of the bottom, all over the bottom squared.

Some people memorize the formula in a different way:

$$\frac{d}{dx}\left( \frac{f(x)}{g(x)}\right) = \frac{f'(x)g(x) - f(x)g'(x)}{(g(x))^2}$$

Verbalize: the derivative of a quotient is the derivative of the top, times the bottom, minus the top, times the derivative of the bottom, all over the bottom squared.

Derivative of a Composite Function

In the composite function $\,f\bigl(g(x)\bigr)\,,$ we can call $\,f\,$ the ‘outer function’ and $\,g\,$ the ‘inner function’.

Note the order of operations indicated by $\,f\bigl(g(x)\bigr)\,$: $\,g\,$ acts on $\,x\,$ first; then $\,f\,$ acts on $\,g(x)\,.$

The Chain Rule tells how to differentiate composite functions:

$$\frac{d}{dx} f\bigl(g(x)\bigr) = f'\bigl(g(x)\bigr)\cdot g'(x)$$

There are two factors in the expression $\,f'\bigl(g(x)\bigr)\cdot g'(x)\,.$ The first factor is $\,f'\bigl(g(x)\bigr)\,,$ and the second factor is $\,g'(x)\,.$

So, we can verbalize the Chain Rule: the derivative of a composite function is the outer function's derivative, evaluated at the inner function, times the derivative of the inner function.

The expression $\,f'\bigl(g(x)\bigr)\,$ is read aloud as ‘$\,f\,$ prime of $\,g\,$ of $\,x\,$’.

The chain rule is used to extend each ‘basic rule’ below to the ‘general rule’.

Notice the pattern to extend from the Basic Rule to the General Rule: replace every $\,x\,$ in the Basic Rule with $\,f(x)\,,$ and then multiply by $\,f'(x)\,.$

How to Differentiate Power Functions

Power functions have a variable base, and a constant in the exponent. The Power Rules tell how to differentiate power functions.

The Basic Rule is called the Simple Power Rule:

$$\frac{d}{dx} x^n = nx^{n-1}$$

The General Rule is called the General Power Rule:

$$\frac{d}{dx} \bigl(f(x)\bigr)^n = n\bigl(f(x)\bigr)^{n-1}f'(x)$$

How to Differentiate the Natural Exponential Function

Exponential functions have a constant base; the variable is in the exponent.

The base of the natural exponential function is the irrational number $\,\text{e}\,$: $f(x) = \text{e}^x$

Basic Rule:

$$\frac{d}{dx} {\text{e}}^x = {\text{e}}^x$$

For this special function (the exponential function with base $\,\text{e}\,$), its derivative is itself! That is, the $y$-value of a point on the graph of $y = {\text{e}}^x$ is the same as the slope of the tangent line at the point!

General rule:

$$\frac{d}{dx} {\text{e}}^{f(x)} = {\text{e}}^{f(x)}\cdot f'(x)$$

How to Differentiate Exponential Functions with Any Allowable Base

Exponential functions have a constant base; the variable is in the exponent.

The variable $\,a\,$ is often used as the base of a general exponential function: $f(x) = a^x$

The allowable bases for exponential functions are $\,a \gt 0\,,$ $\,a\ne 1\,.$

Basic Rule:

$$\frac{d}{dx} a^x = a^x\,\ln a$$

General Rule:

$$\frac{d}{dx} a^{f(x)} = a^{f(x)}(\ln a)\cdot f'(x)$$

Note that $\,\ln\text{e} = 1\,,$ so the constant ‘$\,\ln a\,$’ disappears when the base of the exponential function is the irrational number $\,\text{e}\,.$

How to Differentiate the Natural Logarithmic Function

The natural logarithmic function has base $\,\text{e}\,$:

$$f(x) = \ln x = \log_{\text{e}} x$$

Basic Rule:

$$\frac{d}{dx} \ln{x} = \frac{1}{x}$$

General Rule:

$$\frac{d}{dx} \ln f(x) = \frac{1}{f(x)}\cdot f'(x)$$

The derivatives of logarithmic functions involve the reciprocal of the input.

How to Differentiate Logarithmic Functions with Any Allowable Base

The variable $\,a\,$ is often used as the base of a general logarithmic function: $f(x) = \log_a x$

The allowable bases for logarithmic functions are $\,a \gt 0\,,$ $\,a\ne 1\,.$

Basic Rule:

$$\frac{d}{dx} \log_a{x} = \frac{1}{x\ln a}$$

General Rule:

$$\frac{d}{dx} \log_a f(x) = \frac{1}{f(x)\ln a}\cdot f'(x)$$

Note that $\,\ln\text{e} = 1\,,$ so the constant ‘$\,\ln a\,$’ disappears when the base of the logarithmic function is the irrational number $\,\text{e}\,.$

How to Differentiate the Trigonometric Functions Sine and Cosine

Basic Rules:

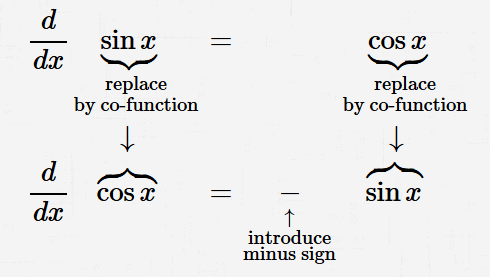
$$ \begin{gather} \frac{d}{dx} \sin x = \cos x\cr\cr \frac{d}{dx} \cos x = -\sin x \end{gather} $$

General Rules:

$$ \begin{gather} \frac{d}{dx} \sin f(x) = \bigl(\cos f(x)\bigr)\cdot f'(x)\cr\cr \frac{d}{dx} \cos f(x) = \bigl(-\sin f(x)\bigr)\cdot f'(x) \end{gather} $$

Sine and cosine are ‘cofunctions’.

Note the pattern to find the derivative of a cofunction: replace each function in the derivative formula by its cofunction, and introduce a minus sign.

How to Differentiate the Trigonometric Functions Tangent and Cotangent

Basic Rules:

$$ \begin{gather} \frac{d}{dx} \tan x = \sec^2 x\cr\cr \frac{d}{dx} \cot x = -\csc^2 x \end{gather} $$

General Rules:

$$ \begin{gather} \frac{d}{dx} \tan f(x) = \bigl(\sec^2 f(x)\bigr)\cdot f'(x)\cr\cr \frac{d}{dx} \cot f(x) = \bigl(-\csc^2 f(x)\bigr)\cdot f'(x) \end{gather} $$

Tangent and cotangent are ‘cofunctions’.

Note the pattern to find the derivative of a cofunction: replace each function in the derivative formula by its cofunction, and introduce a minus sign.

How to Differentiate the Trigonometric Functions Secant and Cosecant

Basic Rules:

$$ \begin{gather} \frac{d}{dx} \sec x = \sec x\,\tan x\cr\cr \frac{d}{dx} \csc x = -\csc x\,\cot x \end{gather} $$

General Rules:

$$ \begin{gather} \frac{d}{dx} \sec f(x) = \bigl(\sec f(x)\,\tan f(x)\bigr)\cdot f'(x)\cr\cr \frac{d}{dx} \csc f(x) = \bigl(-\csc f(x)\,\cot f(x)\bigr)\cdot f'(x) \end{gather} $$

Secant and cosecant are ‘cofunctions’.

Note the pattern to find the derivative of a cofunction: replace each function in the derivative formula by its cofunction, and introduce a minus sign.

How to Differentiate the Inverse Trigonometric Functions

Basic Rules:

$$ \begin{gather} \frac{d}{dx} \arcsin x = \frac{1}{\sqrt{1-x^2}}\cr\cr \frac{d}{dx} \arccos x = \frac{-1}{\sqrt{1-x^2}}\cr\cr \frac{d}{dx} \arctan x = \frac{1}{1+x^2} \end{gather} $$

General Rules:

$$ \begin{gather} \frac{d}{dx} \arcsin f(x) = \frac{1}{\sqrt{1-(f(x))^2}}\cdot f'(x)\cr\cr \frac{d}{dx} \arccos f(x) = \frac{-1}{\sqrt{1-(f(x))^2}}\cdot f'(x)\cr\cr \frac{d}{dx} \arctan f(x) = \frac{1}{1+(f(x))^2}\cdot f'(x) \end{gather} $$

There is alternative notation for the inverse trigonometric functions:

$$ \begin{gather} \arcsin(x) = \sin^{-1}(x)\cr\cr \arccos(x) = \cos^{-1}(x)\cr\cr \arctan(x) = \tan^{-1}(x) \end{gather} $$

Concept Practice

In these exercises, as needed, functions are assumed to be differentiable and to have all required properties.