 Measures of Spread (Part 1)
Measures of Spread (Part 1)
(This page is Part 1. Click here for Part 2.)
You may want to review:
Mean and median are measures of central tendency; that is, they each provide a single number that attempts to describe the center of a collection of data.
However, data can be ‘spread out’ around its ‘center’ in very different ways!
This section explores the three most common measures of spread: range, variance, and standard deviation.
The following data sets all have mean equal to $\,1\,$:
$$ \begin{gather} \cssId{s10}{1,\ \ 1,\ \ 1,\ \ 1,\ \ 1}\cr \cr \cssId{s11}{-1,\ \ 0,\ \ 1,\ \ 2,\ \ 3}\cr \cr \cssId{s12}{-1,\ \ -1,\ \ 1,\ \ 3,\ \ 3} \end{gather} $$These three data sets are pictured below (as pebbles of equal weight on a number line). Notice that each has its balancing point (mean) at $\,1\,,$ but the data is spread about this mean in very different ways:
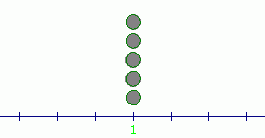
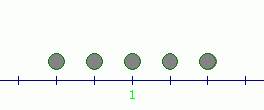
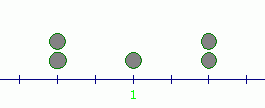
Clearly, the mean does not capture any information about the spread or variability of data about the mean.
First, we discuss the simplest measure of spread—the range.
Let $\ x_{\text{max}}\ $ and $\ x_{\text{min}}\ $ denote the greatest and least numbers in a (finite) data set, respectively.
The range of the data set is the difference: $$ \cssId{s23}{ x_{\text{max}} - x_{\text{min}}} $$
Thus, the range is the difference between the greatest and least numbers in the data set. Since $\, x_{\text{max}}\, $ is always greater than or equal to $\, x_{\text{min}}\,,$ it follows that the range is always greater than or equal to zero.
Examples
Since computation of the range uses only two members from a data set, it is necessarily incomplete in the information that it provides. However, the range is extremely easy to compute.
Another reasonable way to measure the spread takes into account how far each data element is from the mean:
Suppose a data set has mean $\,\bar{x}\,,$ and let $\,x_i\,$ denote an element in this data set.
The deviation of $\,x_i\,$ from the mean is given by the formula:
$$ \cssId{s44}{x_i - \bar{x}} $$From this definition, it is apparent that:
- if a data element is greater than the mean, then its deviation from the mean is positive
- if a data element is less than the mean, then its deviation from the mean is negative
- if a data element is equal to the mean, then its deviation from the mean is zero
Merely summing the deviations from the mean is useless as a measure of spread because the sum of all the deviations is always equal to zero, as the following calculation shows:
$$ \begin{align} &\cssId{s52}{\sum_{i=1}^n\ (x_i - \bar{x})}\cr\cr &\quad\cssId{s53}{=\ (x_1 - \bar{x}) + (x_2 - \bar{x}) + \cdots + (x_n - \bar{x})}\cr\cr &\quad\cssId{s54}{=\ (x_1 + x_2 + \cdots + x_n) - n\bar{x}}\cr\cr &\quad\cssId{s55}{=\ n\cdot \frac{x_1 + x_2 + \cdots + x_n}{n} - n\bar{x}}\cr &\qquad\cssId{s56}{(\text{multiply first part by 1})}\cr\cr &\quad\cssId{s57}{=\ n\bar{x} - n\bar{x}}\cr\cr &\quad\cssId{s58}{=\ 0} \end{align} $$