Loans and Investments (Part 2)

(This page is Part 2. Click here for Part 1.)

Saving for the Future

You are saving for the future. Your initial deposit is $\,\$4100\,.$ Interest is being earned at an annual rate of $\,5\%\,,$ compounded monthly. You will contribute an additional $\,\$120\,$ each month.

(a)  Find the interest earned in the first month.
(b)  Write a recursive formula where $\,u_n\,$ gives the amount saved (principal plus interest) after $\,n\,$ months.
(c)  Then, find the amount saved (principal plus interest) after $\,7\,$ years.
(d)  Find the total amount of money you contributed (principal only) during these $\,7\,$ years.
(e)  Find the total interest earned during these $\,7\,$ years.

Solution

(a) Find the interest earned in the first month

The interest earned in the first month is: $$\cssId{sb18}{(\$4{,}100)(\frac{0.05}{12}) = \$17.08}$$

(b) Write a recursive formula where $\,u_n\,$ gives the amount saved (principal plus interest) after $\,n\,$ months

The recursive formula is: $$ \begin{align} &\cssId{sb21}{u_0 = 4100}\cr &\cssId{sb22}{u_n = (1 + \frac{0.05}{12})u_{n-1} + 120\,,\ \ \text{ for } n \ge 1} \end{align} $$

(c) Find the amount saved (principal plus interest) after $\,7\,$ years

Note that $\,7\,$ years is $\,7(12) = 84\,$ months.

From the calculator, or from the form below: $$\cssId{sb26}{u_{84} = 17853.39}$$

Thus, you have saved (principal plus interest) $\,\$17{,}853.39\,$ after $\,7\,$ years.

The form below computes the amount saved (principal plus interest) after $\,n\,$ equal monthly payments:

• Your initial deposit is $\,u_0\,$ (in dollars).

  That is, $\,u_0\,$ is the amount saved at time zero (the start of your savings program).

• Interest is being earned at an annual rate of $\,i\%\,,$ compounded monthly.

  For example, if the interest rate is $\,5\%\,,$ then $\,i = 5\,.$ That is, $\,i\,$ does not include the percent sign.

• You are contributing an additional $\,\$C\,$ each month.

  For example, if you contribute $\,\$120\,,$ then $\,C = 120\,.$ That is, $\,C\,$ does not include the dollar sign.

• $\,u_n\,$ is the amount saved (principal plus interest) after $\,n\,$ monthly contributions:

  $$ \begin{align} \cssId{sb38}{u(n)}\cr &\cssId{sb39}{= u_n}\cr &\cssId{sb40}{= {\textstyle\bigl(1 + \frac{i/100}{12}\bigr)u_{n-1} + C}\ \text{ for }\ n = 1,2,3,\ldots} \end{align} $$

(d) Find the total amount of money you contributed (principal only) during these $\,7\,$ years

The total amount of money you contributed (principal only) during these $\,7\,$ years is: $$\cssId{sb59}{\$4100 + 7(12)(\$120) = \$14{,}180.00}$$

(e) Find the total interest earned during these $\,7\,$ years

The total interest earned during these $\,7\,$ years is: $$\cssId{sb62}{\$17{,}853.39 - \$14{,}180.00 = \$3,673.39}$$

Using WolframAlpha to Work with Recursive Sequences

Find $\,u_n\,$ for $\,n = 3\cdot 52\,,$ if: $$ \begin{align} &\cssId{sb65}{u_0 = 10,000}\cr &\cssId{sb66}{u_n = (1 + \frac{0.075}{52})u_{n-1} - 20\,,\ \ \text{ for }\ n \ge 1} \end{align} $$

Step 1

Put the information into WolframAlpha:

u(0) = 10000, u(n) = (1 + 0.075/52)*u(n-1) - 20

Step 2

WolframAlpha verifies your input as:

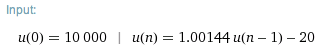
As part of your answer, you get this recurrence equation solution, which is a nonrecursive description of the sequence:

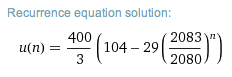
Step 3

If you click on the recurrence equation solution, then WolframAlpha puts it in the input box for you. This is much safer than typing it in yourself!

Step 4

Change the value of $\,n\,$ to the desired value. If the value of $\,n\,$ involves computations, then (to ensure correct order of operations) put it inside parentheses, as shown here:

Step 5

Scroll down to the decimal approximation:

So, if you borrow $\,\$10,000\,$ at a $\,7.5\%\,$ annual interest rate and pay back $\,\$20\,$ per week, then after $\,3\,$ years you will still owe $\,\$9025.14\,.$