Basic Models You Must Know (Part 2)

(This page is Part 2. Click here for Part 1.)

Details on Each of the Basic Models

Each function is now discussed in detail, indicating important properties that you must know. Read the discussion of the identity function carefully; it introduces notation that is not repeated for the subsequent basic models.

The Identity Function, $f(x)=x$

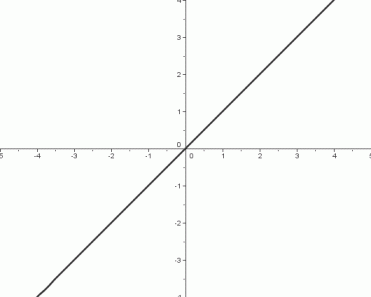
• The identity function takes an input, does nothing to it, and gives back the same thing as its output. That is, the identity function preserves the identity of its input—hence its name is appropriate.
• The domain of the identity function is the set of real numbers:  $\,\text{dom}(f) = \mathbb{R}$
• The range of the identity function is the set of real numbers:  $\,\text{ran}(f) = \mathbb{R}$

End Behavior of the Graph

as $\,x \rightarrow \infty\,,$ $\,y\rightarrow\infty$

Read this aloud as: as $\,x\,$ goes to infinity, $\,y\,$ goes to infinity. This is the right-hand end behavior: as we move farther and farther to the right on the graph, the $\,y$-values of the points are increasing, without bound.

as $\,x\rightarrow -\infty\,,$ $\,y\rightarrow -\infty$

Read this aloud as: as $\,x\,$ goes to negative infinity, $\,y\,$ goes to negative infinity. This is the left-hand end behavior: as we move farther and farther to the left on the graph, the $\,y\,$-values of the points are decreasing, without bound.

There is a convention regarding graphs that you must know. If no endpoints are clearly indicated on the graph (using solid or hollow dots, as in the domain/range discussion in Part 1), then the behavior exhibited at the boundaries of the graph is assumed to continue forever and ever.

The Squaring Function, $\,f(x)=x^2$

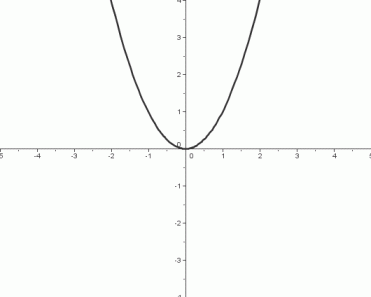
• The squaring function takes an input and squares it (i.e., multiplies it by itself).
• The domain of the squaring function is the set of real numbers:  $\,\text{dom}(f) = \mathbb{R}$
• The range of the squaring function is the set of nonnegative real numbers:  $\,\text{ran}(f) = [0,\infty)$

End Behavior of the Graph

Right-hand end behavior:
as $\,x \rightarrow \infty\,,$ $\,y\rightarrow\infty$

Left-hand end behavior:
as $\,x\rightarrow -\infty\,,$ $\,y\rightarrow \infty$

Important Feature of the Graph

There is a horizontal tangent line at the point $\,(0,0)\,.$ That is, if you imagine yourself walking along the graph, going from left to right, then at the instant you are passing through the point $\,(0,0)\,,$ you will be traveling horizontally.

The Cubing Function, $\,f(x)=x^3$

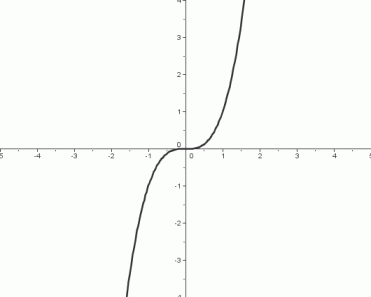
• The cubing function takes an input and cubes it (i.e., raises it to the third power).
• The domain of the cubing function is the set of real numbers:   $\,\text{dom}(f) = \mathbb{R}$
• The range of the cubing function is the set of real numbers:   $\,\text{ran}(f) = \mathbb{R}$

End Behavior of the Graph

Right-hand end behavior:
as $\,x \rightarrow \infty\,,$ $\,y\rightarrow\infty$

Left-hand end behavior:
as $\,x\rightarrow -\infty\,,$ $\,y\rightarrow -\infty$

Important Feature of the Graph

There is a horizontal tangent line at the point $\,(0,0)\,.$ That is, if you imagine yourself walking along the graph, going from left to right, then at the instant you are passing through the point $\,(0,0)\,,$ you will be traveling horizontally.

The Square Root Function, $\,f(x)=\sqrt{x}$

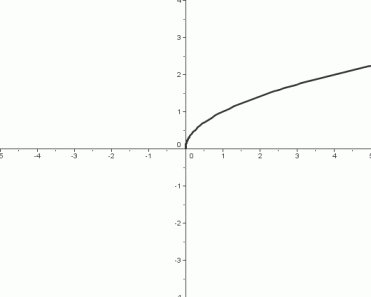
• The square root function takes the square root of an input.
• The domain of the square root function is the set of nonnegative real numbers:   $\,\text{dom}(f) = [0,\infty)$
• The range of the square root function is the set of nonnegative real numbers:   $\,\text{ran}(f) = [0,\infty)$

End Behavior of the Graph

Right-hand end behavior:
as $\,x \rightarrow \infty\,,$ $\,y\rightarrow\infty$

Important Feature of the Graph

There is a vertical tangent line at the point $\,(0,0)\,.$ That is, if you imagine yourself walking along the graph, going from left to right, then at the instant you start off at the point $\,(0,0)\,,$ you will be traveling vertically.

The Absolute Value Function, $\,f(x)=|x|$

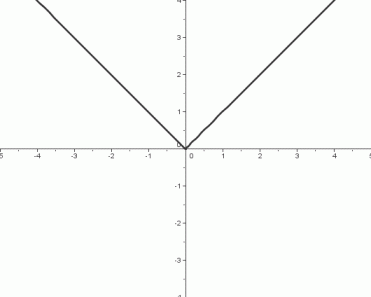
• The absolute value function takes the absolute value of an input. If an input is positive or zero, then it is not changed. If an input is negative, then the function returns its opposite.
• The domain of the absolute value function is the set of real numbers:   $\,\text{dom}(f) = \Bbb R$
• The range of the absolute value function is the set of nonnegative real numbers:   $\,\text{ran}(f) = [0,\infty)$

End Behavior of the Graph

Right-hand end behavior:
as $\,x \rightarrow \infty\,,$ $\,y\rightarrow\infty$

Left-hand end behavior:
as $\,x \rightarrow -\infty\,,$ $\,y\rightarrow\infty$

Important Feature of the Graph

There is a ‘kink’ (i.e., a sharp change in direction) at the point $\,(0,0)\,.$ That is, if you imagine yourself walking along the graph, going from left to right, then at the instant you are passing through the point $\,(0,0)\,,$ you will abruptly change direction.

The Reciprocal Function, $\,\displaystyle f(x)=\frac{1}{x}$

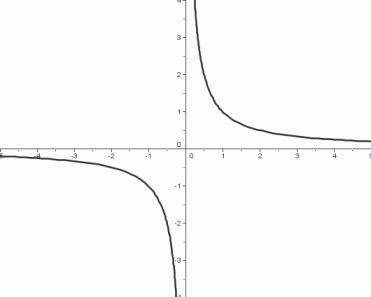
• The reciprocal function takes the reciprocal (i.e., multiplicative inverse) of an input.
• The domain of the reciprocal function is the set of nonzero real numbers: $$\cssId{s102}{\text{dom}(f) = (-\infty,0) \cup (0,\infty)}$$ The symbol ‘$\,\cup\,$’ is the ‘union’ symbol, and is discussed in detail in the section Advanced Set Concepts. For now, it is sufficient to know that ‘$\,\cup\,$’ is used to put two sets together.
• The range of the reciprocal function is the set of nonzero real numbers: $$\cssId{s109}{\text{ran}(f) = (-\infty,0) \cup (0,\infty)}$$

End Behavior of the Graph

Right-hand end behavior:
as $\,x \rightarrow \infty\,,$ $\,y\rightarrow 0$

Left-hand end behavior:
as $\,x \rightarrow -\infty\,,$ $\,y\rightarrow 0$

Behavior Near Zero

Right-hand behavior near zero:
as $\,x \rightarrow 0^{+}\,,$ $y\rightarrow\infty$

The sentence ‘$\ x\rightarrow 0^{+}\ $’ is read aloud as:

$\,x\,$ approaches zero from the right-hand side

This means that the inputs are getting arbitrarily close to zero, coming in from the positive ($\,+\,$) side.

Left-hand behavior near zero:
as $\,x \rightarrow 0^{-}\,,$ $y\rightarrow -\infty$

The sentence ‘$\ x\rightarrow 0^{-}\ $’ is read aloud as:

$\,x\,$ approaches zero from the left-hand side

This means that the inputs are getting arbitrarily close to zero, coming in from the negative ($\,-\,$) side.

Constant Functions, $\,f(x)=k\,,$ for $\,k\in\mathbb{R}$

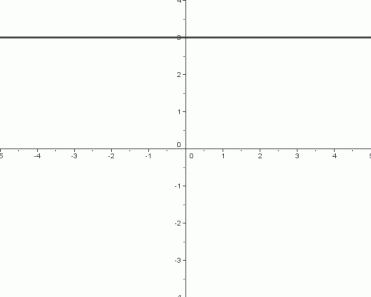
The graph shows the constant function $\,f(x)=3\,.$

• A constant function takes an input, and returns a specific real number—a constant. In the graph above, the function always returns the number $\,3\,.$ Constant functions are extremely boring—they ignore the input, and always return the same output.
• The domain of every constant function is the set of real numbers:   $\text{dom}(f) = \mathbb{R}$
• The range of a constant function is a set containing only one number.   For the constant function shown above: $\text{ran}(f) = \{3\}$

Important Feature of the Graph

Every constant function graphs as a horizontal line.