 Arithmetic with Complex Numbers
Arithmetic with Complex Numbers
You may want to review: Complex Numbers
Whenever you get a new mathematical object (like complex numbers), you need to develop tools to work with the new object.
In this section, you'll learn how to do basic arithmetic and common tasks with complex numbers:
- Square Roots of Negative Numbers
- Powers of $\,i\,$
- Adding and Subtracting Complex Numbers
- Multiplying Complex Numbers
- Finding All Complex Number Solutions for Simple Quadratic Equations
Remember the key fact:
$\,i:=\sqrt{-1}\,,$ so that $\,i^2=-1$
Square Roots of Negative Numbers
Complex numbers allow us to compute the square root of negative numbers, like $\,\sqrt{-4}\,.$
Notice that: $$(2i)(2i) = 4i^2 = 4(-1) = -4$$
Thus, $\,2i\,$ is a (complex) number which, when squared, gives $\,-4\,.$
We write: $$\sqrt{-4}=2i$$
Let $\,p\,$ be a positive real number, so that $\,-p\,$ is a negative real number.
Then: $$ \cssId{s21}{\sqrt{\strut -p} = i\,\sqrt{\strut p}} $$
Some of my students like to think of it this way: You can slide a minus sign out of a square root, and in the process, it turns into the imaginary number $\,i\,$!
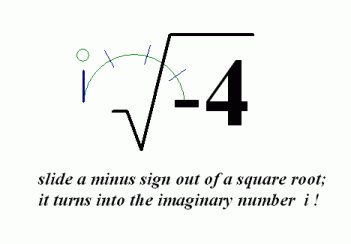
Here are some examples:
-
$\sqrt{-4} = i\sqrt{4} = i2 = 2i\,$
It is conventional to write $\,2i\,,$ not $\,i2\,.$ When there's no possible misinterpretation (see below), write a real number multiplier before the $\,i\,.$
-
$\sqrt{-5} = i\sqrt{5}$
In this situation, it's actually better to leave the $\,\sqrt{5}\,$ after the $\,i\,.$ Why? If you pull the $\,\sqrt{5}\,$ to the front, it can lead to a misinterpretation, as follows:
The numbers $\,\sqrt{5}i\,$ and $\,\sqrt{5i}\,$ are different numbers—look carefully!
In $\ \sqrt{5}i\ ,$ the $\,i\,$ is outside the square root.
In $\ \sqrt{5i}\ ,$ the $\,i\,$ is inside the square root.
Unless you look carefully, however, you might mistake one of these for the other. By writing $\,i\sqrt{5}\,,$ you eliminate any possible confusion.
Two Different Questions; Two Different Answers
Recall these two different questions, with two different answers:
-
What is $\,\sqrt{4}\,$?
Answer: By definition, $\,\sqrt{4} = 2\,.$ The number $\ \sqrt{4}\ $ is the nonnegative number which, when squared, gives $\,4\,.$
-
What are the solutions to the equation $\,x^2 = 4\,$?
Answer: $\,x=\pm 2\,.$ There are two different real numbers which, when squared, give $\,4\,.$
Similarly, there are two different questions involving complex numbers, with two different answers:
-
What is $\,\sqrt{-4}\,$?
Answer: $\sqrt{-4} = 2i\,$
-
What are the (complex) solutions to the equation $\,x^2 = -4\,$?
Answer: $\,x=\pm \sqrt{-4} = \pm 2i\,.$ There are two different complex numbers which, when squared, give $\,-4\,.$
Verifying the second solution: $$\cssId{s56}{(-2i)(-2i) = 4i^2 = 4(-1) = -4}$$
Powers of $\,i\,$
Let's look at powers of $\,i\,$:
| $i^1 = \LARGE \color{green} i$ | $i^2 = \LARGE \color{red} {-1}$ | $i^3 = \LARGE \color{blue} {-i}$ | $i^4 = \LARGE \color{purple} {1}$ |
| $i^5 = \LARGE \color{green} i$ | $i^6 = \LARGE \color{red} {-1}$ | $i^7 = \LARGE \color{blue} {-i}$ | $i^8 = \LARGE \color{purple} {1}$ |
Notice that the same four values occur over and over again: $\,i\,,$ $\,-1\,,$ $\,-i\,,$ and $\,1\,.$ Multiplying by $\,i\,$ causes a $\,90^{\circ}\,$ counter-clockwise rotation (about the origin) in the complex plane!
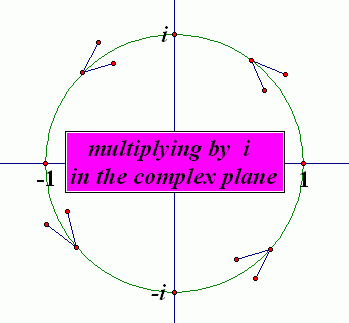
This makes it easy to compute the value of $\,i\,$ raised to any (whole number) power: just write the power as a multiple of four plus remainder, and notice that the remainder determines the final value, as illustrated below:
| $i^{2959}$ | original expression |
| $\ \ = i^{4(739)+3}$ |
How many piles of size $\,4\,$ can we get from $\,2959\,$? First compute $\,2959/4 = 739.75\,$; you get $\,739\,$ piles, with some left over. Take away these $\,739\,$ piles of $\,4\,$ to see what remains: $\,2959 - 4(739) = 3\,,$ so the remainder is $\,3\,.$ Thus, $\,2959 = 4(739) + 3\,.$ This is the name for $\,2959\,$ that we need! |
| $\ \ = i^{4(739)}\cdot i^3$ | Use an exponent law: $\,x^{m+n} = x^nx^m\,$ |
| $\ \ = (i^4)^{739}\cdot i^3$ | Use an exponent law: $\,x^{mn} = (x^m)^n\,$ |
| $\ \ = 1^{739}\cdot i^3$ | since $\,i^4 = 1$ |
| $\ \ = i^3$ | Use the special properties of $\,1\,$; note that the only number in the exponent is the remainder term! |
| $\ \ = -i$ | It's a lot easier to compute $\,i\,$ to the third power, rather than the $\,2959^{\text{th}}\,$ power! Ah, the power of renaming! |
(A careful reader may be concerned about using the laws of exponents with non-real numbers; rest assured that their use here is fine.)
Adding and Subtracting Complex Numbers
Adding and subtracting complex numbers is easy: just work with the real and imaginary parts separately.
Here are some examples, where real terms are colored red and imaginary terms are colored blue:
$$ \begin{align} &\cssId{s103}{(\color{red}{3}\color{blue}{+ 4i}) + (\color{red}{-7}\color{blue}{+ 5i})}\cr &\quad \cssId{s104}{=\ \ \color{red}{3-7} \color{blue}{+ 4i + 5i}}\cr &\quad \cssId{s105}{=\ \ \color{red}{-4} \color{blue}{+ 9i}}\cr\cr &\cssId{s106}{\color{blue}{i} \color{red}{- 3} \color{blue}{+ 2i - 5i} \color{red}{+ 6}}\cr &\quad \cssId{s107}{=\ \ \color{red}{-3 + 6} \color{blue}{+ i + 2i - 5i}}\cr &\quad \cssId{s108}{=\ \ \color{red}{3} \color{blue}{- 2i}} \end{align} $$When doing problems like this, it might be easiest to make two passes through the expression: on the first pass, combine all the real parts; on the second pass, combine all the imaginary parts.
Notice how the distributive law is used in the next example:
$$ \begin{align} &\cssId{s113}{(2+3i) - (1-4i)}\cr &\quad \cssId{s114}{=\ \ 2+3i - 1 + 4i}\cr &\quad \cssId{s115}{=\ \ 1 + 7i} \end{align} $$Precisely, we have:
Let $\,a\,,$ $\,b\,,$ $\,c\,,$ and $\,d\,$ be real numbers, and let $\,i:=\sqrt{-1}\,.$
Then,
$$ \begin{align} &\cssId{s121}{(a+bi)\, + \, (c+di)}\cr &\qquad \cssId{s122}{=\ (a+c) + (b+d)i}\cr\cr &\cssId{s123}{(a+bi)\, - \, (c+di)}\cr &\qquad \cssId{s124}{=\ (a-c) + (b-d)i} \end{align} $$Multiplying Complex Numbers
Multiplying complex numbers is also easy: just use FOIL! For example,
| $(3-4i)(2+5i)$ | original expression |
| $\ \ = 6 + 15i - 8i -20i^2$ | FOIL |
| $\ \ = 6 + 7i - 20(-1)$ | combine like terms; $\,i^2 = -1\,$ |
| $\ \ = 26 + 7i$ | simplify |
Since you'll just think of using FOIL, you certainly won't memorize the following result. It is included here only for completeness:
Let $\,a\,,$ $\,b\,,$ $\,c\,,$ and $\,d\,$ be real numbers, and let $\,i:=\sqrt{-1}\,.$
Then:
$$ \begin{align} &\cssId{s144}{(a+bi)(c+di)}\cr &\qquad \cssId{s145}{=\ (ac-bd) + (ad+bc)i} \end{align} $$