1.5 Using Identified Periodic Components for Prediction
The next example raises a question that is of fundamental importance whenever an analyst wants to use identified periodic components for predictive purposes.
Small numbers are used in the example, for ease of notation.
Example
Suppose that an output list $\,\boldsymbol{\rm y}\,$ is conjectured to be the sum of a $3$-cycle ($\,\boldsymbol{\rm p}\,$) and a $2$-cycle ($\,\boldsymbol{\rm q}\,$). That is,
$$ \boldsymbol{\rm p} + \boldsymbol{\rm q} = \boldsymbol{\rm y}\,, $$or, in list form:
$$ \begin{align} &(p_1,p_2,p_3,p_1,p_2,p_3,\ldots)\cr +\ \ &(q_1,q_2,q_1,q_2,q_1,q_2,\ldots)\cr =\ &(y_1,y_2,y_3,y_4,y_5,y_6,\ldots) \end{align} \tag{1} $$This conjecture may have come from some preliminary data analysis on the already-observed output values $\,\boldsymbol{\rm y}\,$; or from some understanding of the underlying mechanism(s) generating the observed data.
The $\,y_i\,$ values are being observed by the analyst; once a given value is observed, then it is known. The entries $\,p_i\,$ and $\,q_i\,$ in the cycles are unknown.
Based on the observed values of $\,y_i\,,$ it is desired to either support or deny the conjecture that $\,\boldsymbol{\rm y}\,$ is the sum of a $3$-cycle and a $2$-cycle; if supported, it is desired to identify lists $\,\boldsymbol{\rm p}\,$ and $\,\boldsymbol{\rm q}\,$ that can be used to predict future values of $\,\boldsymbol{\rm y}\,.$
By summing and then equating entries in (1), a system of linear equations in the unknowns $\,p_i\,$ and $\,q_i\,$ emerges:
$$ \begin{align} p_1 + q_1 &= y_1\cr p_2 + q_2 &= y_2\cr p_3 + q_1 &= y_3\cr &\vdots \end{align} \tag{2} $$Some linear algebra considerations regarding the linear system just produced are in order.
Since there are $\,5\,$ unknowns ($\,p_1\,,$ $\,p_2\,,$ $\,p_3\,,$ $\,q_1\,,$ and $\,q_2\,$), one needs $\,5\,$ pieces of non-overlapping, non-contradictory information to uniquely determine the $\,5\,$ unknowns. One always needs $\,n\,$ pieces of non-overlapping, non-contradictory information to uniquely determine $\,n\,$ unknowns in a linear system.
However, it has been previously noted that $\,\boldsymbol{\rm p}\,$ and $\,\boldsymbol{\rm q}\,$ can not be uniquely determined, since adding any constant $\,K\,$ to $\,\boldsymbol{\rm p}\,$ and subtracting the same constant $\,K\,$ from $\,\boldsymbol{\rm q}\,$ gives the same sum. Thus, analysis of any system of the form indicated in (2) will not produce a unique solution.
How many pieces of data must the analyst observe, in order to ‘identify’ lists $\,\boldsymbol{\rm p}\,$ and $\,\boldsymbol{\rm q}\,$ that can be used for predictive purposes?
If there is any hope of identifying the $\,p_i\,$ and $\,q_i\,,$ then these unknowns must actually appear in the system: thus, one must observe at least the first three values of $\,\boldsymbol{\rm y}\,.$ This gives the linear system in the five variables ($\,p_1\,,$ $\,p_2\,,$ $\,p_3\,,$ $\,q_1\,,$ and $\,q_2\,$),
$$ \begin{align} p_1 + q_1 &= y_1\cr p_2 + q_2 &= y_2\cr p_3 + q_1 &= y_3\ , \end{align} $$with matrix form
$$ \begin{bmatrix} 1 & 0 & 0 & 1 & 0\cr 0 & 1 & 0 & 0 & 1\cr 0 & 0 & 1 & 1 & 0\cr \end{bmatrix} \begin{bmatrix} p_1\cr p_2\cr p_3\cr q_1\cr q_2 \end{bmatrix} = \begin{bmatrix} y_1\cr y_2\cr y_3 \end{bmatrix}\ , $$and with augmented matrix:
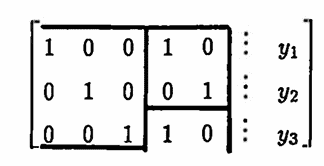
|
$(3)$ |
Pay particular attention to the identity matrices and partial identity matrices that appear in the resulting augmented matrix. Similar patterns will always emerge when investigating sums of periodic lists.
The system in (3) has two degrees of freedom. Once values are chosen for $\,q_1\,$ and $\,q_2\,,$ the remaining values $\,p_1\,,$ $\,p_2\,,$ and $\,p_3\,$ are uniquely determined:
$$ \begin{align} p_1 &= y_1 - q_1\cr p_2 &= y_2 - q_2\cr p_3 &= y_3 - q_1\cr \end{align} $$It is readily checked that the resulting lists $\,\boldsymbol{\rm p}\,$ and $\,\boldsymbol{\rm q}\,$ do indeed sum to give the first $\,3\,$ observed values of $\,\boldsymbol{\rm y}\,$:
$$ \begin{align} &(y_1-q_1,\,y_2-q_2,\,y_3-q_1)\cr + \ \ &(\qquad\, q_1,\qquad\, q_2,\qquad\ q_1)\cr = \ \ &(\qquad\, y_1,\qquad\, y_2,\qquad\, y_3)\ , \end{align} $$regardless of the choices made for $\,q_1\,$ and $\,q_2\,.$
Can the ‘identified’ lists $\,\boldsymbol{\rm p}\,$ and $\,\boldsymbol{\rm q}\,$ be used to predict future values of $\,\boldsymbol{\rm y}\,$? To investigate this question, use the lists $\,\boldsymbol{\rm p}\,$ and $\,\boldsymbol{\rm q}\,$ determined in (3) to ‘predict’ a fourth value of $\,\boldsymbol{\rm y}\,,$ giving:
$$ \begin{align} y_4 &= p_1 + q_2\cr &= (y_1-q_1) + q_2 \end{align} $$Here is the critical observation: the predicted value of $\,y_4\,$ depends on the choices made for $\,q_1\,$ and $\,q_2\,$! That is, different choices of $3$-cycles and $2$-cycles that sum to give the first $\,3\,$ observed values of $\,\boldsymbol{\rm y}\,,$ can lead to different predicted values for $\,y_4\,,$ as illustrated next.
Example
For example, choosing
$$ \begin{gather} y_1 = 1\,,\ \ y_2 = 2\,,\ \ y_3 = 3\,,\cr q_1 = 1\,,\ \text{ and }\ q_2 = 0 \end{gather} $$yields
$$ \begin{gather} p_1 = y_1 - q_1 = 1 - 1 = 0\cr p_2 = y_2 - q_2 = 2 - 0 = 2\cr p_3 = y_3 - q_1 = 3 - 1 = 2\cr \end{gather} $$so that:
$$ \begin{align} &(0,2,2,0) + (1,0,1,0)\cr\cr &\qquad = (\overbrace{1,2,3}^\text{known}, \overbrace{0}^\text{predicted}) \end{align} $$Here, the first three (known) values of $\,\boldsymbol{\rm y}\,$ are obtained; and one ‘predicts’ the value $\,0\,,$ based on the ‘identified’ periodic lists.
Alternatively, choosing the same values for $\,y_1\,,$ $\,y_2\,$ and $\,y_3\,,$ but choosing $\,q_1 = 0\,$ and $\,q_2 = 1\,$ yields
$$ \begin{gather} p_1 = 1 - 0 = 1\cr p_2 = 2 - 1 = 1\cr p_3 = 3 - 0 = 3\cr \end{gather} $$so that:
$$ \begin{align} &(1,1,3,1) + (0,1,0,1)\cr\cr &\qquad = (\overbrace{1,2,3}^\text{known}, \overbrace{2}^\text{predicted}) \end{align} $$Here, the first three (known) values of $\,\boldsymbol{\rm y}\,$ are obtained; and one ‘predicts’ the different value $\,2\,,$ based on the ‘identified’ periodic lists.
Thus, when only $\,3\,$ values of $\,\boldsymbol{\rm y}\,$ have been observed, any ‘identified’ periodic lists are useless for predictive purposes. Different periodic lists can lead to different predicted values.
Suppose that one more piece of data, $\,y_4\,,$ is observed (and hence now known). Then, $\,\boldsymbol{\rm p}\,$ and $\,\boldsymbol{\rm q}\,$ depend on the $\,4\,$ numbers $\,y_1\,,$ $\,y_2\,,$ $\,y_3\,,$ and $\,y_4\,.$
The new system has the augmented matrix:
$$ \begin{bmatrix} 1 & 0 & 0 & 1 & 0 & \vdots & y_1\cr 0 & 1 & 0 & 0 & 1 & \vdots & y_2\cr 0 & 0 & 1 & 1 & 0 & \vdots & y_3\cr 1 & 0 & 0 & 0 & 1 & \vdots & y_4 \end{bmatrix} \tag{4} $$Notation: $\,R'_m = kR_n + R_m$
This augmented matrix is transformed, via Gauss-Jordan elimination, to a matrix for an equivalent system that is much easier to analyze. The notation
$$R'_m = kR_n + R_m$$is used to denote the row operation:
Replace (Row $m$)
by
($k$ times Row $n$) added to (Row $m$)
That is:
$$ \overbrace{R'_m}^\text{new Row $m$} = \overbrace{kR_n}^\text{$k$ times Row $n$} + \overbrace{R_m}^\text{old Row $m$} $$The row operations below transform the matrix in (4) to reduced row-echelon form:
$$ \begin{gather} R'_4 = -R_1 + R_4\cr \begin{bmatrix} 1 & 0 & 0 & 1 & 0 & \vdots & y_1\cr 0 & 1 & 0 & 0 & 1 & \vdots & y_2\cr 0 & 0 & 1 & 1 & 0 & \vdots & y_3\cr 0 & 0 & 0 & -1 & 1 & \vdots & -y_1 + y_4 \end{bmatrix}\cr\cr \text{(zero first column)} \end{gather} $$$$ \begin{gather} R'_4 = -R_4\cr \begin{bmatrix} 1 & 0 & 0 & 1 & 0 & \vdots & y_1\cr 0 & 1 & 0 & 0 & 1 & \vdots & y_2\cr 0 & 0 & 1 & 1 & 0 & \vdots & y_3\cr 0 & 0 & 0 & 1 & -1 & \vdots & y_1 - y_4 \end{bmatrix}\cr\cr \text{(leading $1$ in last row)} \end{gather} $$
$$ \begin{gather} R'_3 = -R_4 + R_3\cr \begin{bmatrix} 1 & 0 & 0 & 1 & 0 & \vdots & y_1\cr 0 & 1 & 0 & 0 & 1 & \vdots & y_2\cr 0 & 0 & 1 & 0 & 1 & \vdots & -y_1 + y_4 + y_3\cr 0 & 0 & 0 & 1 & -1 & \vdots & y_1 - y_4 \end{bmatrix}\cr\cr \text{(zero fourth column)} \end{gather} $$
$$ \begin{gather} R'_1 = -R_4 + R_1\cr \begin{bmatrix} 1 & 0 & 0 & 0 & 1 & \vdots & y_4\cr 0 & 1 & 0 & 0 & 1 & \vdots & y_2\cr 0 & 0 & 1 & 0 & 1 & \vdots & -y_1 + y_4 + y_3\cr 0 & 0 & 0 & 1 & -1 & \vdots & y_1 - y_4 \end{bmatrix}\cr\cr \text{(zero fourth column)} \end{gather} \tag{5} $$
The system in (5) has one degree of freedom. Once a value is chosen for $\,q_2\,,$ the values of $\,p_1\,,$ $\,p_2\,,$ $\,p_3\,$ and $\,q_1\,$ are uniquely determined:
$$ \begin{align} p_1 &= y_4 - q_2\cr p_2 &= y_2 - q_2\cr p_3 &= -y_1 + y_4 + y_3 - q_2\cr q_1 &= y_1 - y_4 + q_2\cr \end{align} $$Summing the ‘identified’ components, and using this sum to predict the next value of $\,\boldsymbol{\rm y}\,$ gives:
$$ \small{ \begin{alignat}{6} &(& y_4-q_2&,&\,y_2-q_2&,& -y_1+y_4+y_3-q_2&,&\, y_4-q_2&,& y_2-q_2&)&\cr + \ &(& y_1-y_4+q_2&,&q_2&,& y_1-y_4+q_2&,& q_2&,&\, y_1-y_4+q_2&)&\cr = \, &(& y_1 &,&y_2&,& y_3&,& y_4&,& y_2+y_1-y_4&)&\cr \end{alignat} } $$The critical observation is that the predicted value for $\,y_5\,,$ $\, y_5 = y_2 + y_1 - y_4\,,$ is independent of the choice of $\,q_2\,.$
Indeed, since each entry in $\,\boldsymbol{\rm p}\,$ is decreased by $\,q_2\,,$ and each entry in $\,\boldsymbol{\rm q}\,$ is increased by $\,q_2\,,$ all predicted values of $\,\boldsymbol{\rm y}\,$ will be independent of $\,q_2\,.$
The example just completed points out some interesting facts.
If data is indeed a sum of a $3$-cycle and a $2$-cycle, then, having $\,4\,$ pieces of data is ‘enough’ to use any identified components for prediction, in the following sense: there will still be an infinite number of periodic components that could sum to give the first four observed values of $\,\boldsymbol{\rm y}\,,$ but, no matter what components are chosen, they will yield the same predicted values for $\,\boldsymbol{\rm y}\,.$
From a practical point of view, this type of information is vitally important. Suppose that (say, based on preliminary data analysis), it is conjectured that observed data is a sum of a $p$-cycle and a $q$-cycle. IF:
- $p\,$ and $\,q\,$ are appropriately related (see Theorem 1);
- the observed data is truly a sum of a $p$-cycle and a $q$-cycle;
- enough data has been observed (see Theorem 1); and
- the investigator is able to identify any $p$-cycle and $q$-cycle that sum to give the observed data;
then these cycles can be used for prediction. It will not matter if they are indeed the ‘right’ cycles or not; since any choice yields the same predicted values.
Suppose that $\,\boldsymbol{\rm y}\,$ is a sum of a $p$-cycle and a $q$-cycle, where $\,p\,$ and $\,q\,$ are positive integers satisfying $\,p = kq+1\,$ for a positive integer $\,k\,. $
If $\,\boldsymbol{\rm p}\,$ and $\,\boldsymbol{\rm q}\,$ are any $\,p\,$ and $q$-cycles (respectively) that sum to give the first $\, p + q - 1\,$ observed values of $\,\boldsymbol{\rm y}\,,$ then $\,\boldsymbol{\rm p}\,$ and $\,\boldsymbol{\rm q}\,$ can be used to predict future values of $\,\boldsymbol{\rm y}\,.$
The proof is constructive, and gives an algorithm for producing all possible $\,p\,$ and $q$-cycles that can sum to produce $\,\boldsymbol{\rm y}\,.$
It is shown that each entry of the $p$-cycle, $\,\boldsymbol{\rm p}\,,$ must have an additive constant $\,K\,,$ and that each entry of the $q$-cycle, $\,\boldsymbol{\rm q}\,,$ must have an additive constant $\,-K\,,$ thus proving that predicted values are independent of the particular choice of components $\,\boldsymbol{\rm p}\,$ and $\,\boldsymbol{\rm q}\,.$
In what follows, the notation$\,I_n\,$ is used for the $\,n\times n\,$ identity matrix; and the notation $\,0_{m,n}\,$ is used for the $\,m\times n\,$ zero matrix.
Let $\,p\,$ and $\,q\,$ be positive integers with $\,p = kq+1\,$ for a positive integer $\,k\,.$ Let $\,\boldsymbol{\rm p}\,$ and $\,\boldsymbol{\rm q}\,$ denote the $p$-cycle and $q$-cycle, respectively, with entries
$$ \boldsymbol{\rm p} = (x_1,x_2,x_3,\ldots,x_p,x_1,x_2,\ldots) $$and
$$ \boldsymbol{\rm q} = (w_1,w_2,\ldots,w_q,w_1,w_2,\ldots)\ , $$and suppose that the first $\,p+q-1\,$ values of $\,\boldsymbol{\rm y}\,$ have been observed. The augmented matrix below is used to solve for the unknown values of $\,x_i\,$ and $\,w_i\,$:
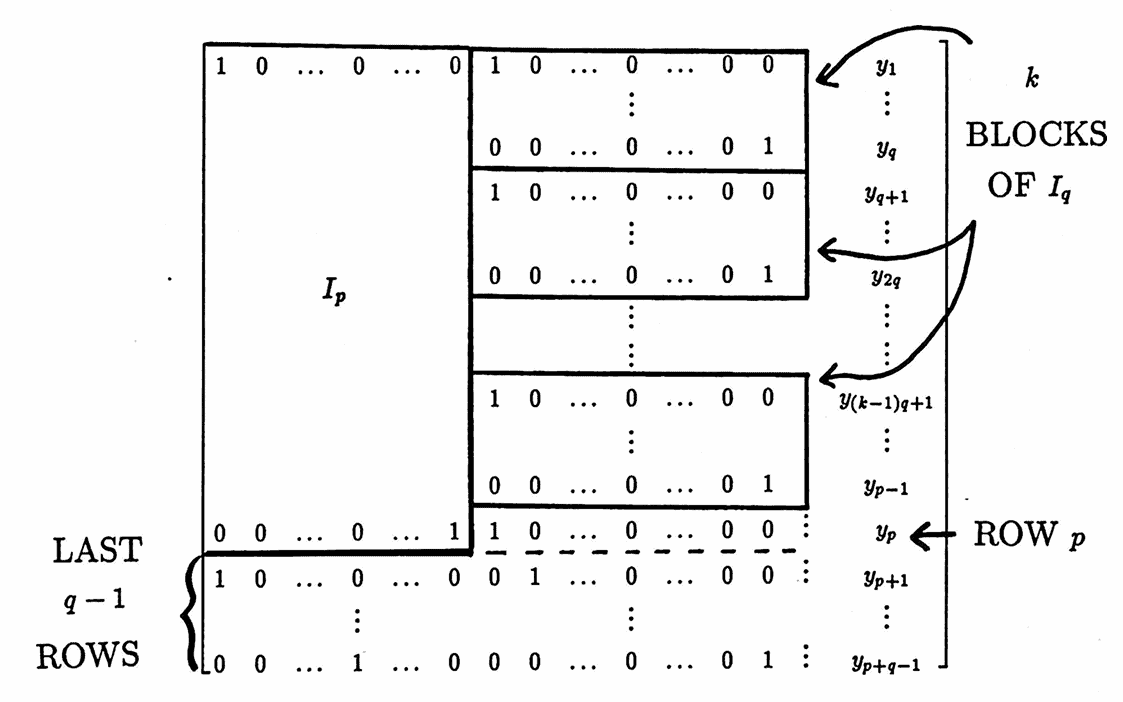
The first $\,p\,$ rows already have leading ones. Use these leading ones to zero out the last $\,q-1\,$ rows, via the row operations:
$$R'_{p+i} = -R_i + R_{p+i}\,,\ 1\le i\le q-1$$This does not affect the first $\,p\,$ rows, but gives the new last $\,q-1\,$ rows:
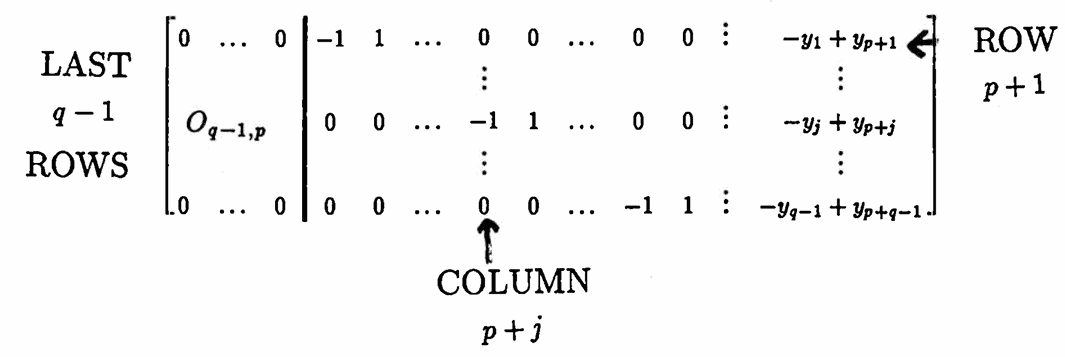
Next, get leading ones in these last $\,q-1\,$ rows, via the row operations:
$$ R'_{p+j} = -R_{p+j}\ , \ \ 1\le j\le q-1 $$This gives the new last $\,q-1\,$ rows:
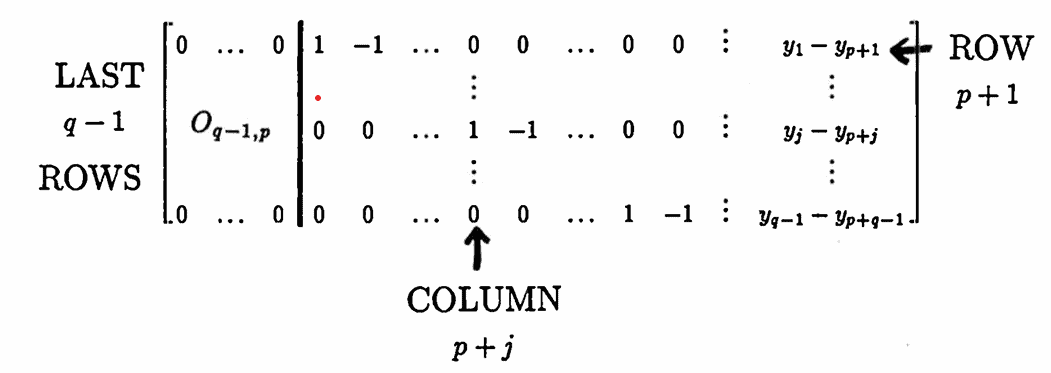
Next, use the leading one in row $\,p+1\,$ to zero out the $\,p+1\,$ column, via the row operations:
$$ R'_{jq+1} = -R_{p+1} + R_{jq+1}\ ,\ \ 0\le j\le k $$Observe that $\,kq + 1 = p\,.$ The first $\,(p + q - 1)\times p\,$ submatrix is not affected by any future row operations, and is not shown. The remaining matrix becomes:
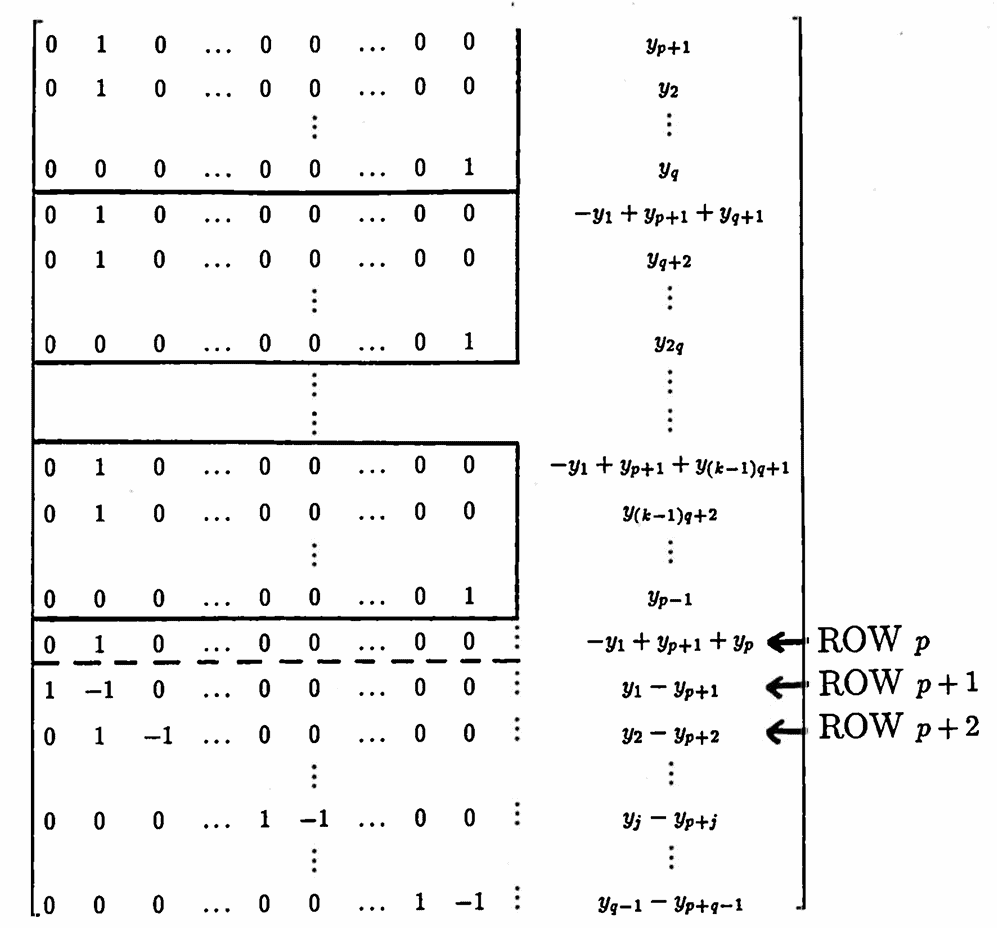
Next, use the leading one in row $\,p+2\,$ to zero out the $\,(p+2)$-column, via the row operations:
$$ \begin{gather} R'_{jq+1} = -R_{p+2} + R_{jq+1}\ ,\ \ 0\le j\le k\ ,\cr\cr R'_{jq+2} = -R_{p+2} + R_{jq+2}\ ,\ \ 0\le j\le k-1\ , \end{gather} $$and
$$ R'_{p+1} = R_{p+2} + R_{p+1} $$The resulting matrix is:
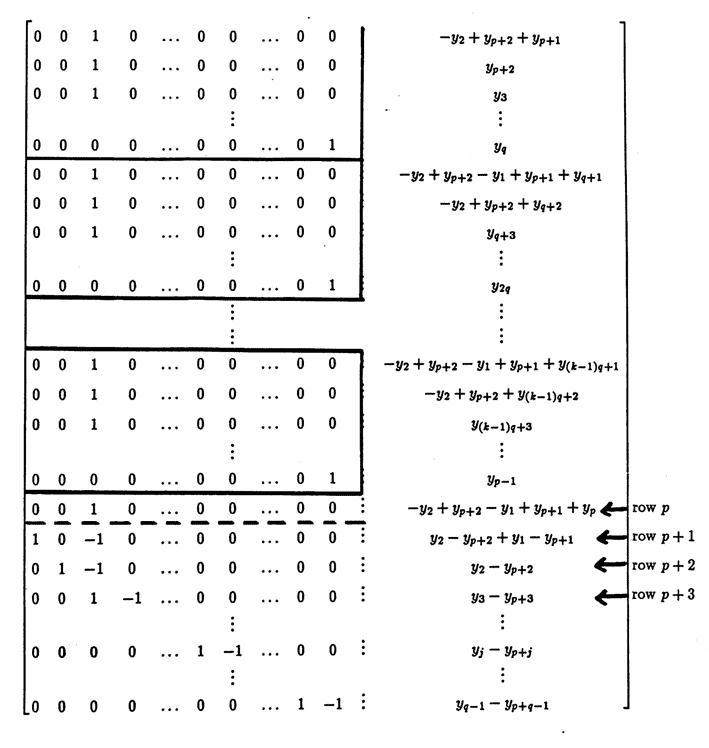
Continuing in this fashion, use the leading one in row $\,p+m\,$ to zero out the $\,p+m\,$ column, via the row operations
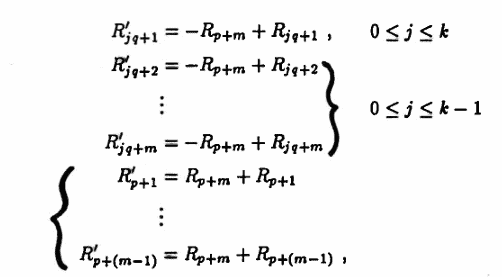
for $\,m = 3,\ldots,q-1\,$; applying this entire set of row operations first for $\,m = 3\,,$ then for $\,m = 4\,,$ and continuing until $\,m = q - 1\,.$
The resulting augmented matrix is shown below. For simplicity, the right-most column makes use of the notation $\,f_i\,,$ where
$$f_i := f_i(y_1,\ldots,y_{p+q-1})$$is an expression that depends on the numbers $\,y_1\,$ through $\,y_{p+q-1}\,,$ for $\,i = 1,\ldots,p+q-1\,.$ The particular form of these expressions is not necessary to the desired conclusion. Instead, the important observation is the $(p+q)$-column of $1$’s and $-1$’s:
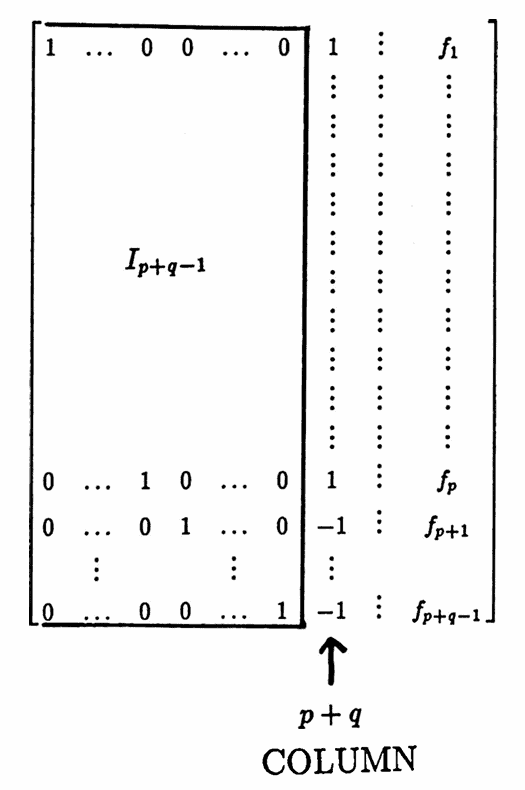
The equivalent system represented by this augmented matrix has one degree of freedom. Once a choice is made for $\,w_q\,,$ the remaining unknowns $\,x_1,\ldots,x_p\,$ and $\,w_1,\ldots,w_{q-1}\,$ are uniquely determined:
$$ \begin{gather} x_1 = f_1 - w_1\cr \vdots\cr x_p = f_p - w_q\cr\cr w_1 = f_{p+1} + w_q\cr \vdots\cr w_{q-1} = f_{p+q-1} + w_q \end{gather} $$Since each entry of $\,\boldsymbol{\rm p}\,$ is decreased by $\,w_q\,,$ and each entry of $\,\boldsymbol{\rm q}\,$ is increased by $\,w_q\,,$ the sum $\,\boldsymbol{\rm p} + \boldsymbol{\rm q}\,$ is uniquely determined by the numbers $\,y_1\,$ through $\,y_{p+q-1}\,,$ and hence future values of the sum are uniquely determined. $\blacksquare$
It is interesting to note the following:
Let $\,p\,,\,q\,$ and $\,k\,$ be positive integers with $\,p = kq + 1\,.$ Then, $\,p\,$ and $\,q\,$ are relatively prime.
Proof of Proposition
Suppose for contradiction that $\,p\,$ and $\,q\,$ have a common factor other than $\,1\,.$ That is, suppose there exists a positive integer $\,j\ne 1\,$ for which both $\,p= jx\,$ and $\,q = jy\,$; here, $\,x\,$ and $\,y\,$ denote the remaining primes in the prime decompositions of $\,p\,$ and $\,q\,,$ respectively.
The following list of equivalent equations is then obtained:
$$ \begin{align} &p= kq + 1\cr\cr &\quad \iff jx = k(jy) + 1\cr\cr &\quad \iff j(x-ky) = 1\cr\cr &\quad \iff x - ky = \frac 1j \end{align} $$Since $\,x\,,$ $\,k\,$ and $\,y\,$ are integers, and the integers are closed under addition and multiplication, $\,x - ky\,$ is an integer. However, $\,\frac 1j\,$ is not an integer.
Thus, the last equation $\,x - ky = \frac 1j\,$ is false. By hypothesis, however, the first equation $\,p= kq + 1\,$ is true. This gives the desired contradiction. $\blacksquare$
Thus, the requirements on $\,p\,$ and $\,q\,$ in Theorem 1 force $\,p\,$ and $\,q\,$ to be relatively prime.
The next section provides a thorough investigation of the sine and cosine functions. These functions have been of great historical importance in the context of periodicity. Also, they will become important at the end of Chapter 2 and in Chapter 3, when studying the periodogram of a data set, and mathematical filters.
The chapter closes with a discussion of historical contributions in the search for hidden periodicities.