 Solving Absolute Value Equations
Solving Absolute Value Equations
Need some simpler practice with absolute value and related concepts first?
- Simplifying Basic Absolute Value Expressions
- Solving Simple Absolute Value Sentences
- Solving Sentences involving ‘Plus or Minus’
If you're going through this entire online Algebra I course, then you already know that I love WolframAlpha.
Well, WolframAlpha allows you to create widgets to share its amazing computational power! You can play with the widget below, before learning to solve absolute value sentences yourself. It can also be useful in checking your work.
WolframAlpha Widget
See that ‘WolframAlpha widget’? It has a starting equation already in place, which happens to be an example from this page. Go ahead and press the ‘Submit’ button—and behold the power of WolframAlpha!
When you press ‘Submit’, a pop-up window opens; you can move it around to keep it nearby while you're reading the lesson. When you're done exploring, just close the pop-up.
Have fun playing with the widget! Type in any absolute value equation or inequality; I like to press ‘Enter’ instead of clicking the ‘Submit’ button. (There is a vertical bar ‘ | ’ for absolute value somewhere on your keyboard—look around!)
If you want, copy-and-paste absolute value sentences from this page. You can even copy-and-paste from the randomly-generated exercises and worksheets. Or, start with these simple sentences:
|x| = 3
|x| < 3
|x| <= 3
|x| > 3
|x| >= 3
Now, let's talk about the concepts involved in solving absolute value equations:
Translating the Theorem
Recall first that normal mathematical conventions dictate that ‘$\,|x| = k\ $’ represents an entire class of sentences, including the members
$|x| = 2$
$|x| = 5.7$
$|x| = \frac{1}{3}$
The variable $\,k\ $ changes from sentence to sentence, but is constant within a given sentence.
Also recall that ‘$\,x=\pm k\ $’ is a shorthand for ‘$\,x = k\,$ or $\,x = -k\,$’.
When you see a sentence of the form $\,|x| = k\ $, here's what you should do:
- Check that $\,k\,$ is a nonnegative number (zero, or greater than zero).
- The symbol $\,|x|\,$ represents the distance between $\,x\,$ and $\,0\,.$
- Thus, you want the numbers $\,x\,,$ whose distance from $\,0\,$ is $\,k\,.$
- You can walk from $\,0\,$ in two directions: to the right, or to the left. Walk to the right a distance $\,k\,,$ and you get to the number $\,k\,.$ Walk to the left a distance $\,k\,,$ and you get to the number $\,-k\,.$
- Thus, $\,|x| = k\ $ is equivalent to $\,x = k\ \text{ or }\ x = -k\,,$ which goes by the shorthand $\,x=\pm k\,.$
- Equivalent sentences are completely interchangeable, and you can use whichever is easiest to work with. In this case, you're getting rid of the troublesome absolute value in exchange for a less-troublesome ‘plus or minus’ sign.
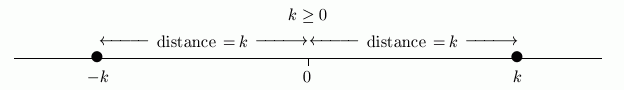
Recall that ‘$\iff$’ is a symbol for ‘is equivalent to’.
The power of the sentence-transforming tool
$$\cssId{s71}{|x| = k \iff x = \pm k}$$goes far beyond solving simple sentences like $\,|x| = 5\,$!
Since $\,x\,$ can be any real number, you should think of $\,x\,$ as merely representing the stuff inside the absolute value symbols. Thus, you could think of rewriting the tool as:
$$ \cssId{s76}{|\text{stuff}| = k \iff \text{stuff} = \pm k} $$See how this idea is used in the following examples:
Example
| $|2 - 3x| = 7$ | original equation |
| $2-3x = \pm 7$ | check that $\,k\ge 0\,$; use the theorem |
| $2-3x = 7\ \text{ or }\ 2-3x = -7$ | expand the plus/minus |
| $-3x = 5\ \text{ or }\ -3x = -9$ | subtract $\,2\,$ from both sides of both equations |
| $\displaystyle x = -\frac{5}{3}\ \text{ or } x = 3$ | divide both sides of both equations by $\,-3\,$ |
It's a good idea to check your solutions:
$|2 - 3(-\frac{5}{3})|\ \overset{\text{?}}{=}\ 7$
$|2 + 5| = 7$
Check!
$|2 - 3(3)|\ \overset{\text{?}}{=}\ 7$
$|2 - 9| = 7$
Check!
Example
| $5 - 2|3 - 4x| = -7$ | original equation |
| $-2|3 - 4x| = -12$ | subtract $\,5\,$ from both sides |
| $|3 - 4x| = 6$ | divide both sides by $\,-2\,$ |
| $3 - 4x = \pm 6$ | check that $\,k\ge 0\,$; use the theorem |
| $3 - 4x = 6 \text{ or } 3 - 4x = -6$ | expand the plus/minus |
| $-4x = 3\ \text{ or }\ -4x = -9$ | subtract $\,3\,$ from both sides of both equations |
| $\displaystyle x = -\frac{3}{4}\ \text{ or }\ x = \frac{9}{4}$ | divide both sides of both equations by $\,-4\,$ |
Example
Concept Practice
Solve the given absolute value equation. Write the result in the most conventional way.
For more advanced students, a graph is available. For example, the equation $\,|2 - 3x| = 7\,$ is optionally accompanied by the graph of $\,y = |2 - 3x|\,$ (the left side of the equation, dashed green) and the graph of $\,y = 7\,$ (the right side of the equation, solid purple). In this example, you are finding the values of $\,x\,$ where the green graph intersects the purple graph.
Click the ‘Show/Hide Graph’ button to toggle the graph.